14.10.21 Matrizen#

Beispiel mit Lebensmitteln

Schoko

Erdnuss

Gummibärchen

Fett

36

31

0,5

Kohlenhydrate

48

40

77

Eiweis

6

14

7

Salz

0,04

2,28

0,07

Frage: wie viel (fett, ..., salz) haben 400g Schoko, 200g Erdnüsse und 500g Gummis zusammen? $\( Fett: \\ Portionen(100g):v = \left(\begin{array}{c} 4 \\ 2 \\ 5 \end{array}\right) , fett= \left(\begin{array}{c} 36 \\ 31 \\ 0,5 \end{array}\right) \\ \implies <v,fett> = 4*36 + 2*31 + 5*0,5 = 208,5 \)$

wenn man das für alle bestandteile wiederholt -> Matrix

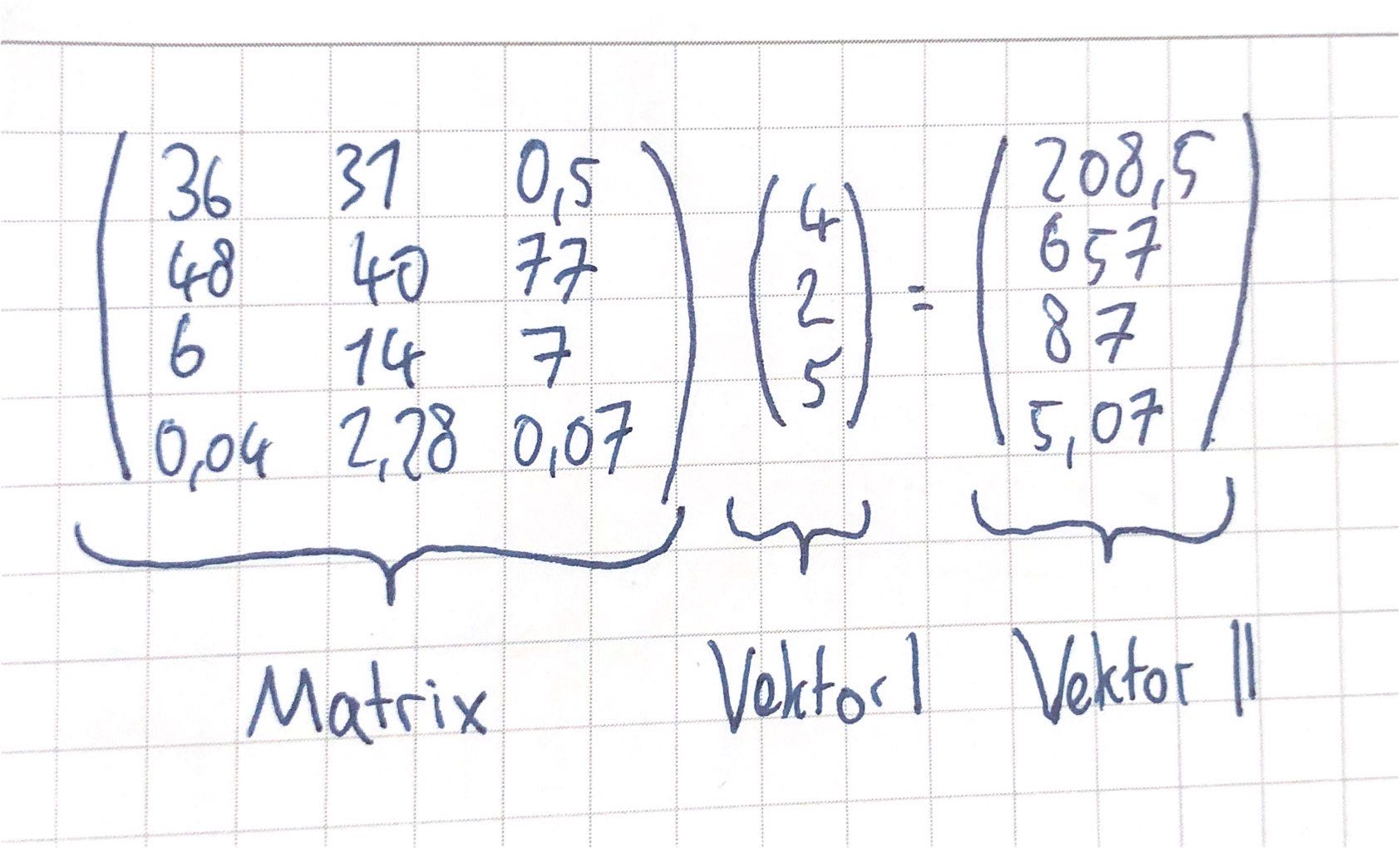
scan 21-10-14 10-50-40

  • Zeilenlänge der Matrix muss = Spaltenlänge des Vektor 1

  • Spaltenlänge Matrix = Spaltenlänge Vektor 2

Matrizennotation:

Definition: rechteckiges Schema mit n Zeilen und m Spalten mit Elementen \(a_{ij}\)

scan 21-10-14 11-13-40

Merke:

  • 1ter Index = Zeile bis m , Indexbezeichnung i

  • 2ter = Spalte bis n, Indexbezeichnung j

\(y_i = a_{i1} * x_1 + a_{i2} * x_2 + ... + a_{im} * x_m\) = mathematische Schreibweise von A * x = y

Matrix beschreibt lineare Abbildung von \(\mathbb{R}^m \rightarrow \mathbb{R}^n \)

Merke zum Rechnen: \(A*e_j\) = j-te Spalte von A (Einheitsvektoren)

Eigenschaften der Matrix:

  • Linearität: multi von Vektor und Matrix = lineare Abbildung

    • Beispiel: Verdoppelt man Produktion, doppelt so viele Rohstoffe

      \(Ax = y \\ A(2x) = 2y = 2(Ax)\)

Transponierte Matrix#

Transponieren = Vertauschen von Zeilen und Spalten einer Matrix

Beispiel: $\( \left( \begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 5 \\ \end{array}\right)^T = \left( \begin{array}{rrr} 1 & 0 \\ 2 & 1 \\ 3 & 5 \\ \end{array}\right) \)$ Bemerkungen:

  • Doppelt Transponieren -> Ursprungsmatrix

  • wenn A quadratisch und \(A = A^T \implies\) A ist symmetrisch

    • Beispiel: \( \left( \begin{array}{rrr} 1 & 5 & 7 \\ 5 & 2 & 6 \\ 7 & 6 & 3 \\ \end{array}\right) \)

  • da Vektoren = (n,1)-Matrizen: Transponierung von Vektor => Spaltenvektor wird Zeilenvektor

  • Nullmatrix= matrix nur aus Nullen

  • Einheitsmatrix I= Matrix aus Eigenvektoren \(\left( \begin{array}{rrr} 1 & 0 & ... & 0\\ 0 & 1 & ... & 0 \\ \vdots & \vdots & \ddots\\ 0 & 0 & & 1 \\ \end{array}\right)\)

​

Rechenoperationen:

  • Addition / Subtraktion : elementweise Addieren / subtrahieren (gleiche Dimension benötigt!)

    • Note: 2 Matrizen sind gleich wenn A - B = 0

  • Multiplikation mit Skalar: elementweise multiplizieren

Matrizenmultiplikation $\( \text{Notation: }C=AB \ mit \ c_{i,j}=\sum_{l=1}^ka_{i,l}b_{l,j} \)$

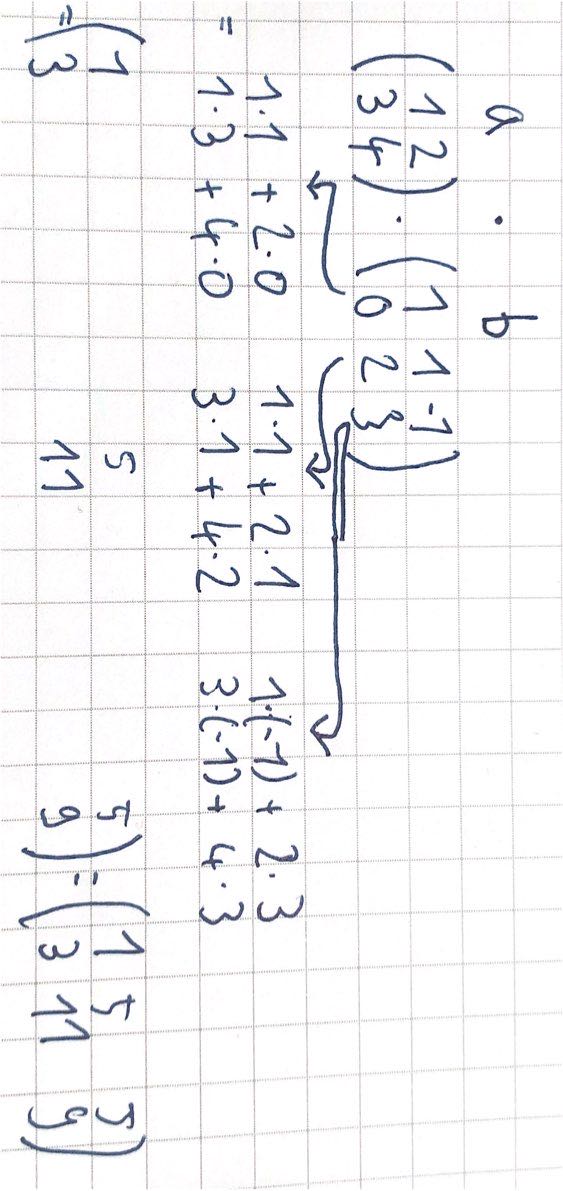
  • Beispiel: scan 21-10-14 11-47-32

Bemerkungen

  • nötig: Anzahl Spalten A = Anzahl Zeilen B (verkettet)

  • Produkt C : Anzahl Zeilen wie A , Anzahl Spalten wie B

Achtung: \(A*B \neq B*A \)(nicht kommutativ) aber A(BC) = (AB)C (assoziativ)