25.11.2021 Graphische Lösung

Beispiel 108

Produktion von zwei Produkten \(x_1,x_2\)

• \(x_1, x_2 \ge 0\)

• Gewinn \(G(x_1,x_2) = 3 x_1 + 4 x_2\)

• Beschränkungen : \(\frac{1}{4}x_1 + \frac{1}{2}x_2 \le 2\) und \(\frac{3}{4}x_1 + \frac{1}{2}x_2 \le 3\)

=> System von Gleichungen

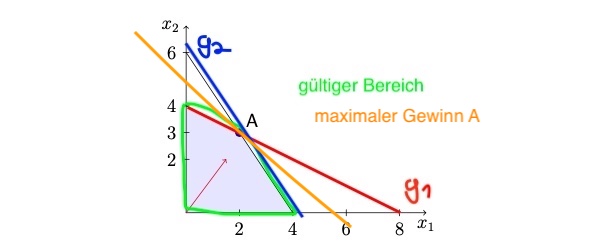
merke: Optimum liegt in Ecke von zulässigem Bereich an Schnittpunkt g1, g2

Berechnung:

Beispiel 109

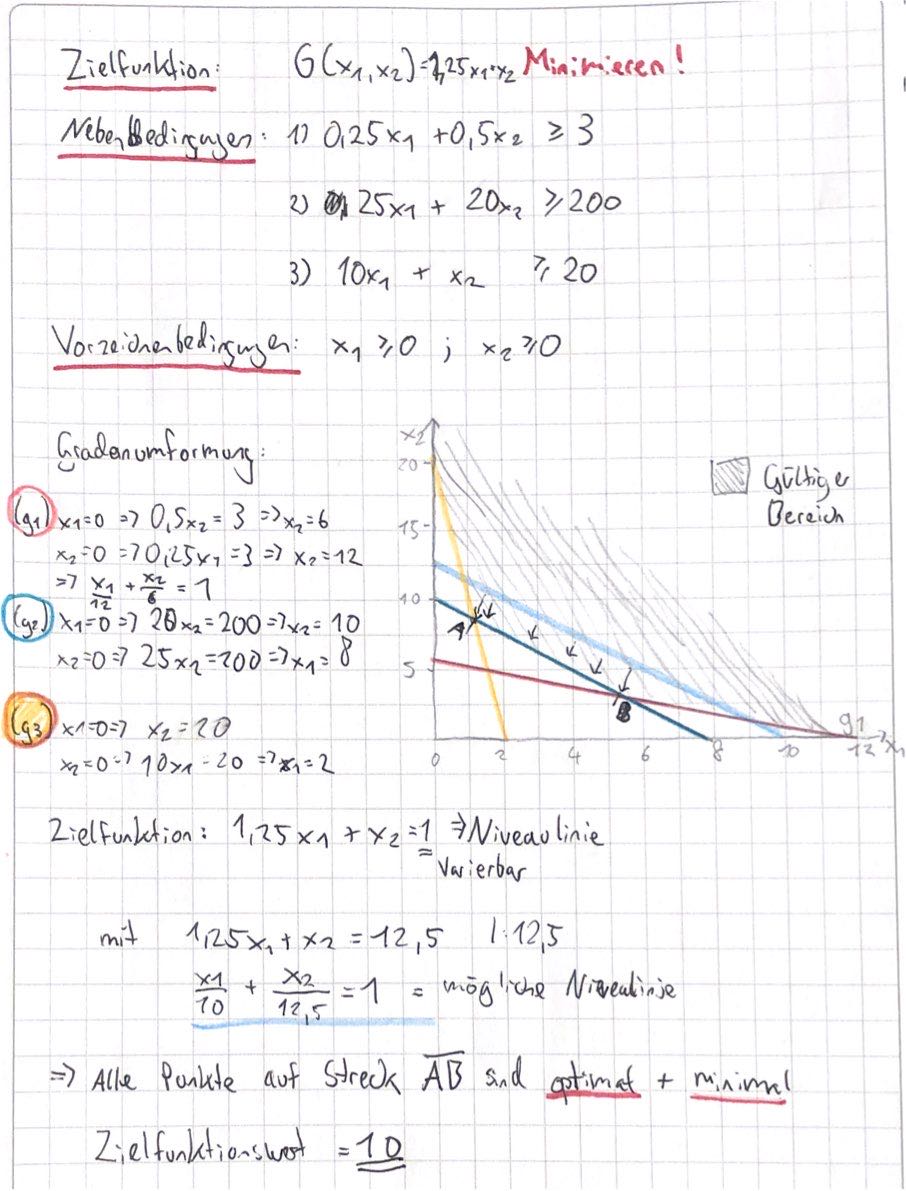
Konvexe Menge

Konvexe Menge: Menge Z heißt konvex, wenn Verbindungsstrecke von Punkten \(x,y \in Z\) vollständig in Z

Verbindungsstrecke: im n= 2: \(\alpha_1 x + \alpha_2 y\) mit \(\alpha_1 + \alpha_2 = 1\)

allg. für m Vektoren \(x_i\): \(\sum_{i=1}^m \alpha_i x_i\) mit \(\sum_{i=1}^m \alpha_i = 1\) = Konvexkombination

jeder Punkt in konvexer Menge durch Konvexkombination darstellbar

Beispiele:

• Dreiecke

• \(\mathbb{R}^n\), da es eine Fläche / Raum beschreibt

• Gegenbeispiel: Viereck mit einem Winkel > 180°

Eigenschaften

• Durchschnitt zweier konvexer Mengen A, B ist konvex (\(A \cap B\))

konvexe Hülle: die Hülle einer nicht-konvexen Menge, die alle Verbindungstrecken hinzugefügt hat (also dann konvex ist)

Beispiel: ein nicht-konvexes Viereck M und die Hülle dazu: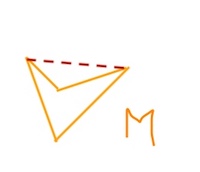

Polyeder: eine durch lineare Ungleichungen beschränkte Menge; immer konvex!

ein beschränktes Polyeder ist Polytop (beschränkt = endliche Menge)

Polyeder (unbeschränkt)	Polytop (beschränkt)