25.10.21 Inverse

Rang: Anzahl Zeilen einer Matrix die linear unabhängig sind,

= Anzahl Stufen übrig

Beispiel 51 Skript:

und dazugehörige Lösung des linearen Systems :

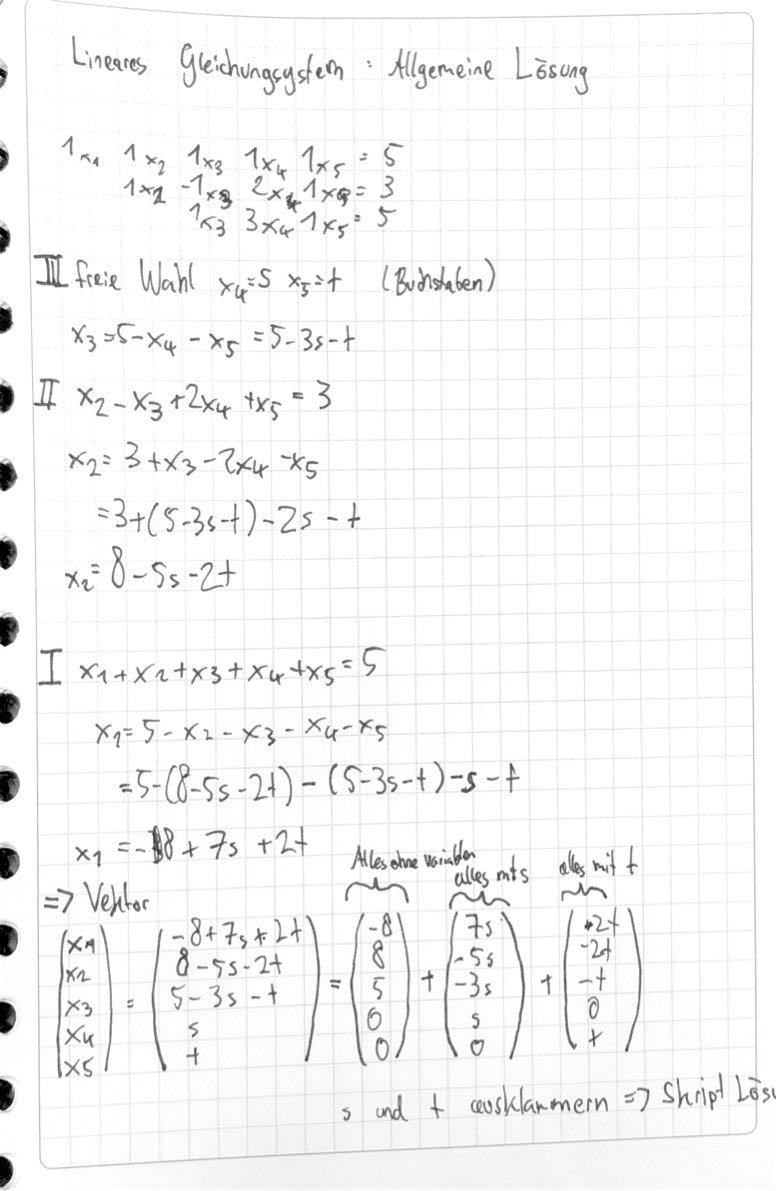
=> Lernen: Allgemeines System in beide Richtungen: lösen und nachweisen, dass es unabhängig ist

Matrixinverse

Definition: zu einer Matrix A mit rang(A)=n ( kann) existiert eine Inverse Matrix \(A^{-1}\)

mit \(A^{-1} A = I\) (Einheitsmatrix)

existiert eine Inverse so heißt quadratische Matrix regulär, wenn nicht singulär

Bildung der Inversen bei 2x2 Matrix:

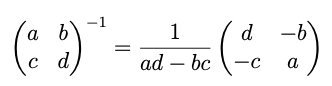
Merke: wenn ad-bc = 0, dann funktionierts natürlich nicht!

bei größeren Matrizen: Gauß-Jordan-Verfahren:

• alles unterhalb der Diagonalen Nullen erzeugen (links nach rechts)

• alles oberhalb der Diagonalen nullen

3x3 Matrix Uff:

Videoerklärung von Daniel Jung

=> Anwendungsbeispiel : Leontief-Modell