01.11.2022 Konvergenz#
Solow und Empirie#
Vorhersagen#
Vorhersage des Pro-Kopf-Einkommens anhand der Faktoren des Solow Modells
\(A\) = Technologielevel
\(s\) = Sparquote
\(n\) = Bevölkerungswachstum
\(u\) = Bildungsjahre
Annahmen:
\(\alpha, \psi, \delta, g\) sind konstant über alle Länder hinweg
alle Länder sind im Steady State
Indien - USA#
Vergleich (1969-2008) |
Indien |
USA |
|---|---|---|
s |
0.241 |
0.202 |
n |
0.017 |
0.011 |
u |
4.23 |
13.24 |
\(a=\frac{1}{3}, \psi = 0.1, \delta+g = 0.075\)
Ergebnis: unter Annahme gleicher Technologie hat Indien 43% des BIP p.P von USA
real: Indien hat 10% des BIP p.P
Bedeutung der Technologie A#
Berechnung: implizit aus Produktionsfunktion
wird als Solow-Residuum bezeichnet = alles was nicht durch Faktoren abgedeckt wird
oft wird mit relativem zu USA gearbeitet \(\hat{A}_i = \frac{A_i}{A_{US}}\)
Synthetische Beispielländer: (im Vergleich zu US)
und dann Berechnung:
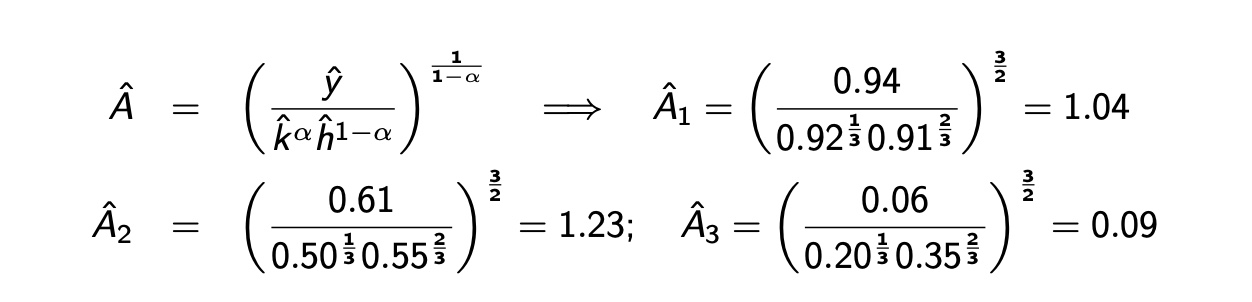
anhand der realen Welt: 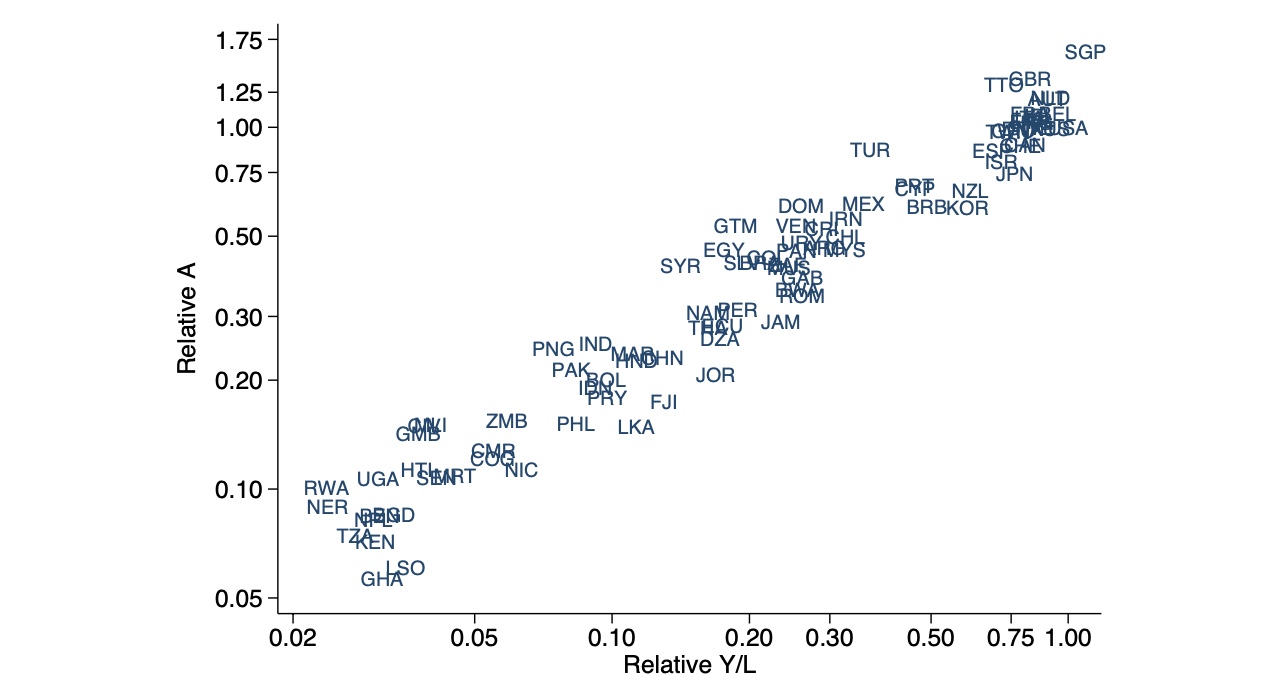
=> wir sehen, dass dieses Residuum fast die gesamten Unterschiede abdeckt
Zerlegung#
die reichsten Länder sind 40 Mal so reich wie ärmste
Zerlegung des Faktors:
Sparquote = 2
Humankapital = 2
Residuum = 10
\(\hat{A}\) =measure of our ignorance
=> Solow Modell ist nicht besonders geil
Wachstumsunterschiede#
ärmere Länder sind noch nicht im Steady State
sie sollten sowohl technoligischen Fortschritt als auch Kapitalakkumulation haben
entwickelte Länder haben nur ersteres
Beta-Konvergenz#
= unbedingte Konvergenz
=> negativer Zusammenhang von BIP p.P und Wachstumsrate
empirisch anhand Regression bestimmt
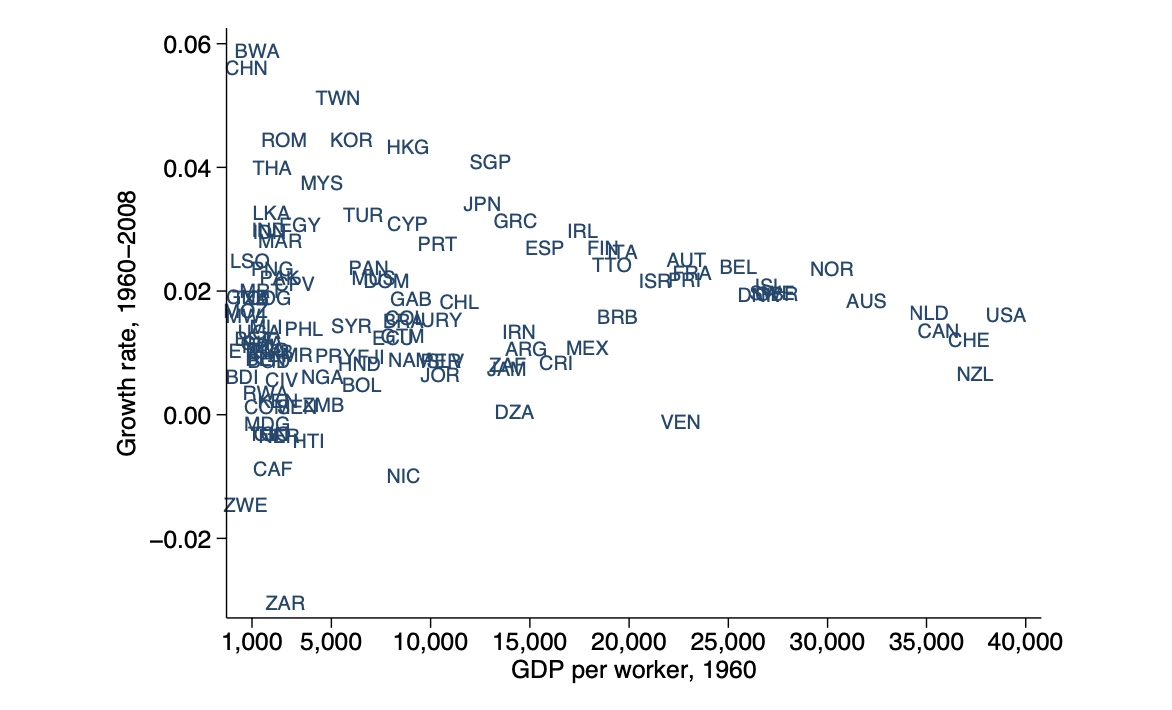
=> funktioniert nicht, da nicht alle Länder gleichen Steady State haben
bedingte Beta-Konvergenz#
Länder mit ähnlichem Steady State ansehen
bspw. entwickelte Volkswirtschaften (OECD)
ähnliches A und h
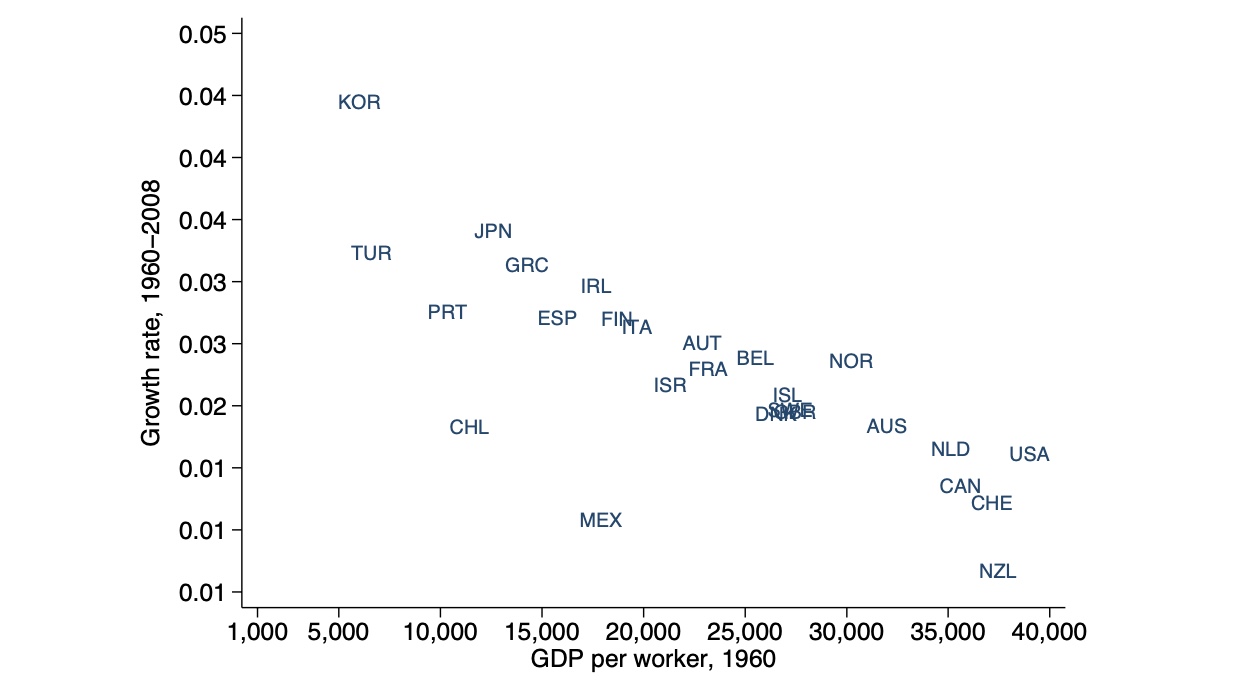
Club Konvergenz#
Es gibt 2 Arten von Ländern auf der Welt (arm und reich)
dazwischen gibt es eine Middle Income Trap
=> früher eher ja, heute eher nein
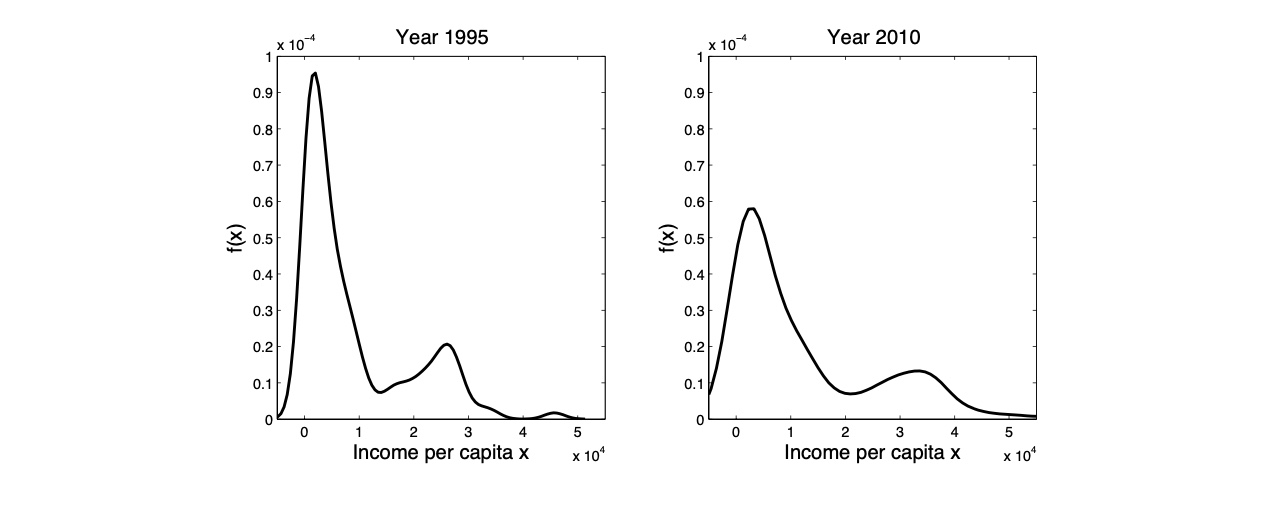
Fazit zu Konvergenz#
! Klausurrelevant !
unbedingte Beta-Konvergenz (alle gleicher Steady State) = nein
bedingte Beta Konvergenz = eher ja
sigma Konvergenz (Rückgang der Varianz von Einkommen) = nein
Club Konvergenz = heute eher weniger
Poverty Traps#
Armutsfalle: Selbstverstärkender Mechanismus, wodurch Länder auf niedrigem Niveau verbleiben
Gründe:
geringe Sparquoten (weil geringes Einkommen)
kein Kapitalaufbau (Krieg, Konflikte etc)
Kapitalflucht
Produktionsfunktion ist komplexer als Cobb-Douglas
S-förmige Produktionsfunktion: 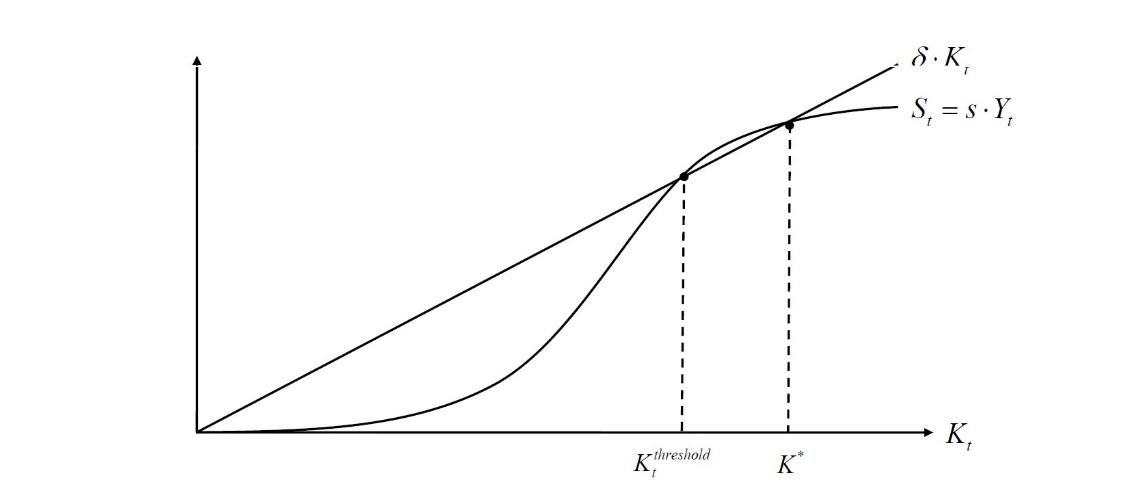
erst ab Treshold ist es gewohnte konkave Funktion und Steady State \(K^*\)
darunter sind Abschreibungen immer höher als Investitionen
= Steady State bei quasi 0
aber seit 1960 (fast) keine Länder ohne Wachstum
nur regional (schwer zugängliche Gebiete) oder temporär (Kriegszeiten etc.)
Übung 2#
Aufgabe 1#
a) $\( g = \frac{y_t}{y_0}^{1/T} - 1 \)$ jährliche Wachstumsrate China = 4.95, USA = 1.89
c) Erreichen China USA: $\( y_c * (1+g_c)^n = y_{us} * (1+g_{us})^n \\ \Big(\frac{1+g_{us}}{1+g_c}\Big)^T = \frac{y_{us}}{y_{c}}\\ T \cdot ln\Big(\frac{1+g_{us}}{1+g_c}\Big) = ln \Big(\frac{y_{us}}{y_{c}}\Big)\\ \to T = \frac{ln(\frac{y_{us}}{y_{c}})}{ln(\frac{1+g_{us}}{1+g_c})} \)$ = 51.28 Jahre
d) $\( y_c * (1+g_c)^{31} = y_{us} * (1+g_{us})^{31} \\ (1+g_c)^{31} = \frac{y_{us}}{y_c} * (1+g_{us})^{31} \\ g_c = (\frac{y_{us}}{y_c})^{1/31} * (1+g_{us})^{31} -1 \)$ = 7%
Aufgabe 2#
Vergleich zwischen diskreter und kontinuierlicher Wachstumsrate:
= Taylor Approximation
Verlgeichstabelle einfügen!
je kleiner das absolute Wachstum, desto geringer die Unterschiede!
Aufgabe 4#
Wachstumsrate: $\( ln(Y) = ln\Big(X^a * (\frac{U}{V})^b\Big) \\ = ln(X^a) + ln(U^b)-ln(V^b) \\ = a * ln(X) + b * ln(U) - b * ln(V) \\ \frac{\partial ln(Y)}{\partial ln(t)} = a \frac{\partial ln(X)}{\partial ln(t)} + b*\Big(\frac{\partial ln(U)}{\partial ln(t)}-\frac{\partial ln(V)}{\partial ln(t)}\Big) \)$
Aufgabe 5#
Wachstumsraten vor Steady State $\( \dot{k} = sy-\delta k \\ k^* = \Big(\frac{s}{\delta}\Big)^{\frac{1}{1-a}} \\ y^* = (k^*)^a = \Big(\frac{s}{\delta}\Big)^{\frac{a}{1-a}} \)$ Wachstum von k und y im Steady State = 0