02.12.2022 Versicherungen#
Versicherung als Anwendung auf Risikoentscheidungen (Lotteriebeispiel)
Nachfrage nach Versicherungen#
Annahme: Individuum kennt:
Ausgangsvermögen \(w_0\)
Schdenswahrscheinlichkeiot p
Vermögensverlust L
Prämie = Schadenswahrscheinlichkeit * Schadenssumme => \( p \times A\)
Situation |
Kein Unfall |
Unfall |
|---|---|---|
Vermögen (mit Vers.) |
\(w_0\) |
\(w_0 - L\) |
**Vermögen (ohne Vers.) ** |
\(w_0- p \cdot A\) |
\(w_0 - pA-L+A\) |
für risikoaverses I.: im Optimum A = L (Vollversicherung)
Annahem: aktuarisch faire Prämie: kostenlose Bewegung von Vermögen zwischen den Zuständen
Versicherungsmärkte#
wie funktionieren Versicherungsmärkte
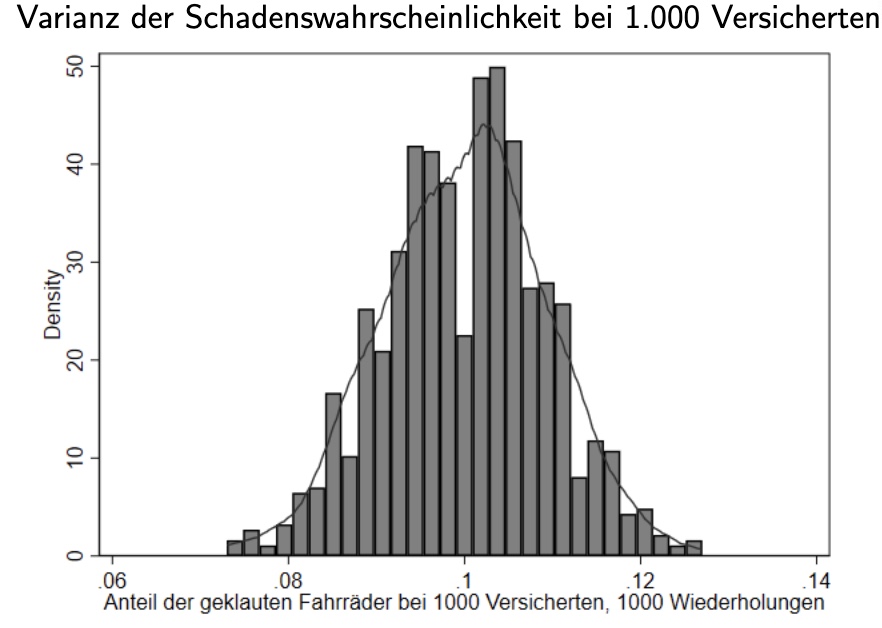
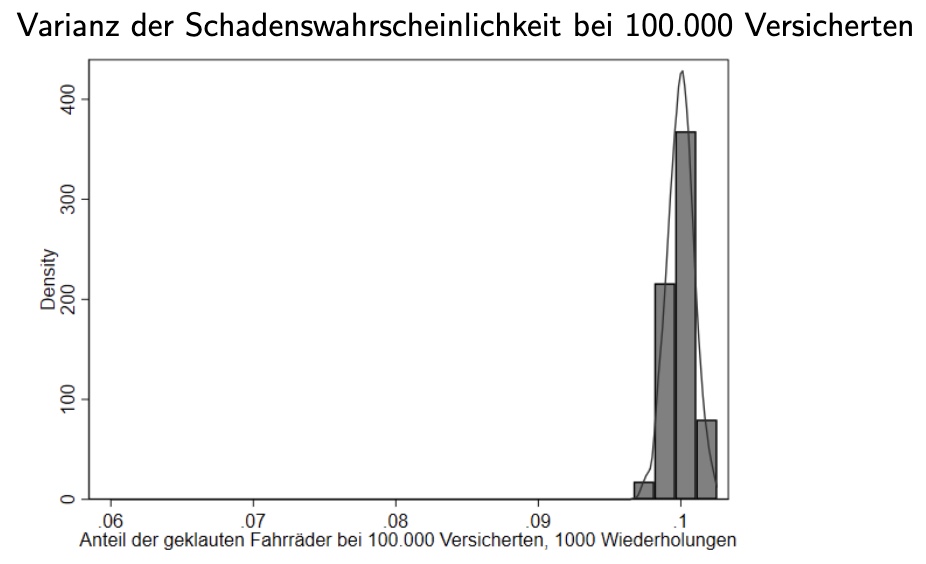
Risk-Pooling#
Zusammenfassung von individuellen Risiken zu Gruppen
Gesetz der großen Zahlen minimiert das Risiko zu Eintreten mit bekannter Sicherheit
Risiko wird beherrschbar
Beispiel:
Schaden eines Fahrraddiebstahls Bernoulli Verteilung mit p Wahrscheinlihckeit
n unabhängige Diebstähle = Binomialverteilung \((n,p)\)
Erwartungswert = \(n \times p\)
ohne Versicherung |
Versicherung |
|---|---|
|
|
Risk Spreading#
bei zusammenhängenden Risiken wie Erdbeben etc. funktioniert Pooling nicht!
Einspringen von Staat
Verteilung von einzelnen auf viele (Steuerzahler)
Risk Transfer#
Transferierung von Risiken zwischen Indivudeen aufgrund unterschiedlicher Aversität
bisher nur Art der Risikoaversion (konvex, konkav, linear)
jetzt Maß der Aversion
Arrow Pratt Maß: absolute Risikoaversion
relative Risikoaversion: $\( r_R(x) = \frac{xu''(x)}{u'(x)} \)$ Beispiel:
2 Indivuen mit Nutznefunktion: \(u(w) = ln(w)\)
Individuum 1: \(w=200.000\), 50% Risiko von Verlust 100.000
Individuum 2: \(w=2.000.000\)
Risikoprämie für Person 1:
Erwartungswert: \(EV = 150000\)
Erwartungsnutzen: \(0,5 \ln(200.000)+0,5\ln(100.000) = 11,859\)
Sicherheitsäquivalent:
\(U(CE) = EU \to ln(CE) = 11,859\)
\(CE = e^{11,859} = 141.350,8\)
Risikoprämie: \(R = EV-CE = 150.000- 141.350= 8649\)
Wann würde Person 2 das Risiko übernehmen wollen?
\(EV = 1.950.000\)
\(EU = 0,5 \ln(2.000.000)+0,5 \ln(1.950.000) = 14,483\)
\(CE = e^{14,483} = 1,949.337,2\)
\(R = 1.950.000 - 1,949.337,2 = 662,75\)
Vergleich der Risikoprämien
Risikoprämie 1: 8649€ (Bereitschaft Risiko abzugeben)
Risikoprämie 2: 662,75€ (Bereitschaft Risiko aufzunehmen)
Asymmetrische Informationsverteilung#
Verschiedene Indivdueen haben andere Risiken:
eine Person hat 3 Schlösser am Rad
die andere schließt nicht an
Problem:
Versicherung kennt nicht Einzelrisikos
sie nimmt also Prämie im Mittelwert
Lohnt nicht für geringrisijo-Personen
steigende Preise -> Teufelskreis
Moral Hazard#
Verhaltensänderung der Versicherten
Ex-Ante: vor Eintritt des Schadens mehr Risiko
Ex-post: nach Eintritt des Schadens teurere Behandlung
erhöht Kosten für Versicherung