01.11.2022 Anleihenmarkt#
Erinnerung:
Preis und Effektivzins = negativer Zusammenhang
Wichtig ist reale Verzinsung = abhängig von Inflationserwartungen
Zinsbildung#
Beispiel:
Nullkuponanleihe, einer Periode Laufzeit
F = 1000
Unterschiedliche Punkte der Nachfragekurve:
mit Ausgedachten Nachfragen nach Bonds = \(B^d\)
\(P = 950, i= \frac{F-P}{P}=\frac{1000-950}{950} = 0.053, B^d = 100 \gets \text{Annahme}\)
\(P = 900, i= \frac{F-P}{P} = 0.111, B^d = 100 \gets \text{Annahme}\)
…
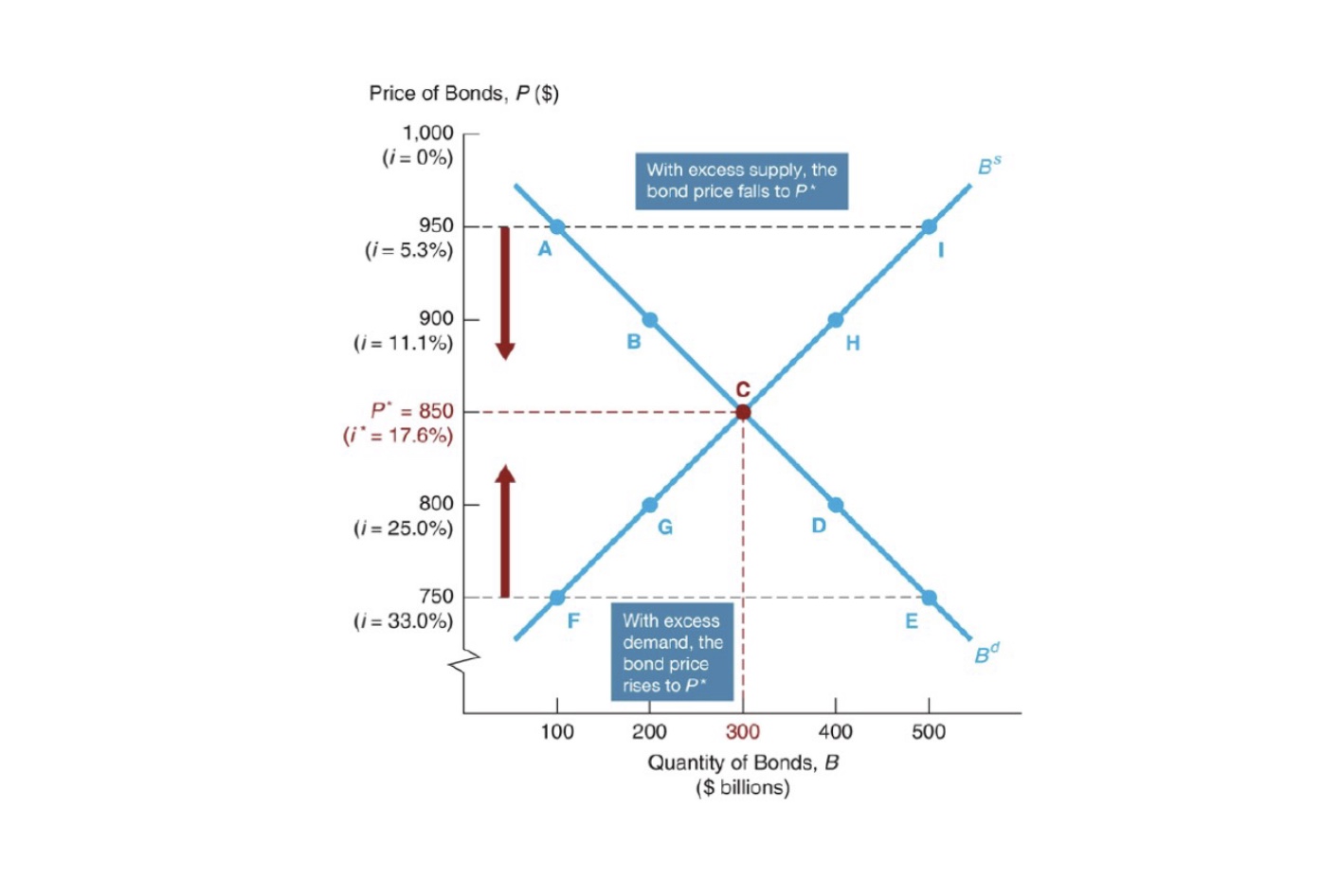
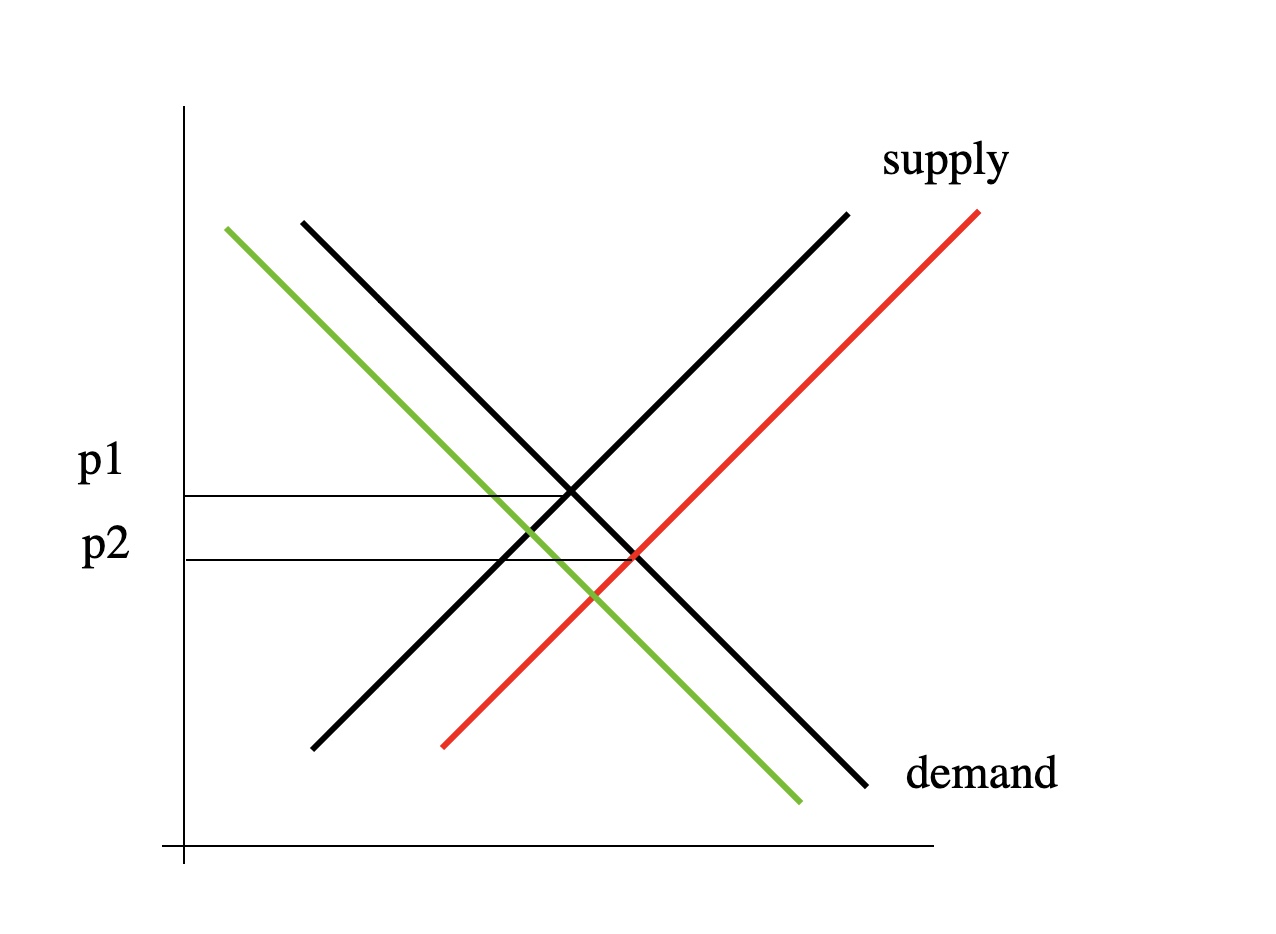
Nachfrage:
niedriger der Preis = höhere Nachfrage (höhere Zinsen)
niedriger Preis = niedrigeres Angebot
Verschiebung der Kurve#
Bisher: nur entlang der Kurven
Jetzt: Verschiebung der Kurven durch externe Faktoren
Verschieben der Nachfrage
Konjunktur = Kurve nach rechts
Inflation = Wert der Auszahlung sinkt = Kurve nach links
Verschieben Angebot
Inflation = Wert der Rückzahlung sinkt = Kurve nach rechts
Profitabilität steigt = Kurve nach links
Inflationserwartungen und Markt 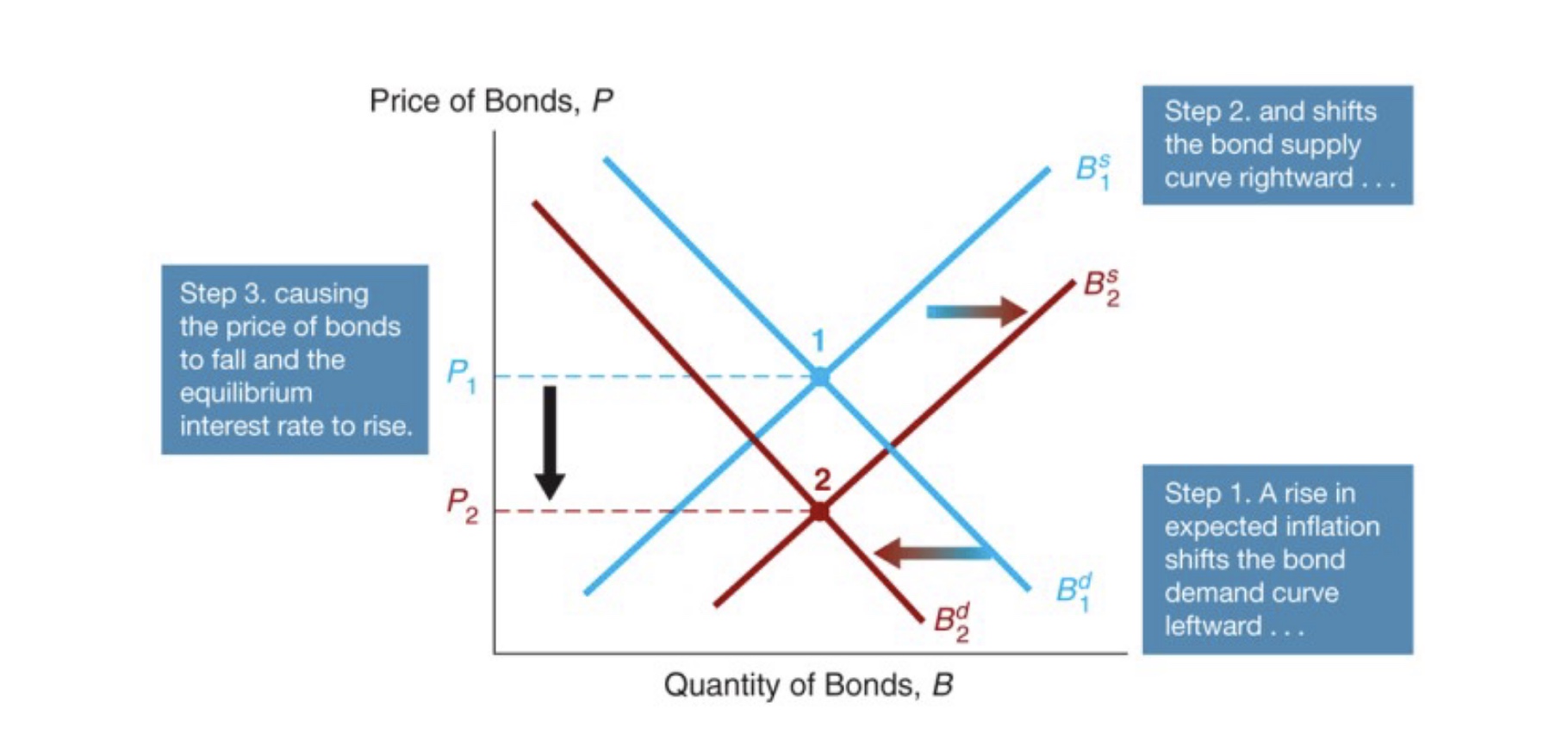
Fischer Effekt empirisch belegt: Inflationserwartungen und Zinsen 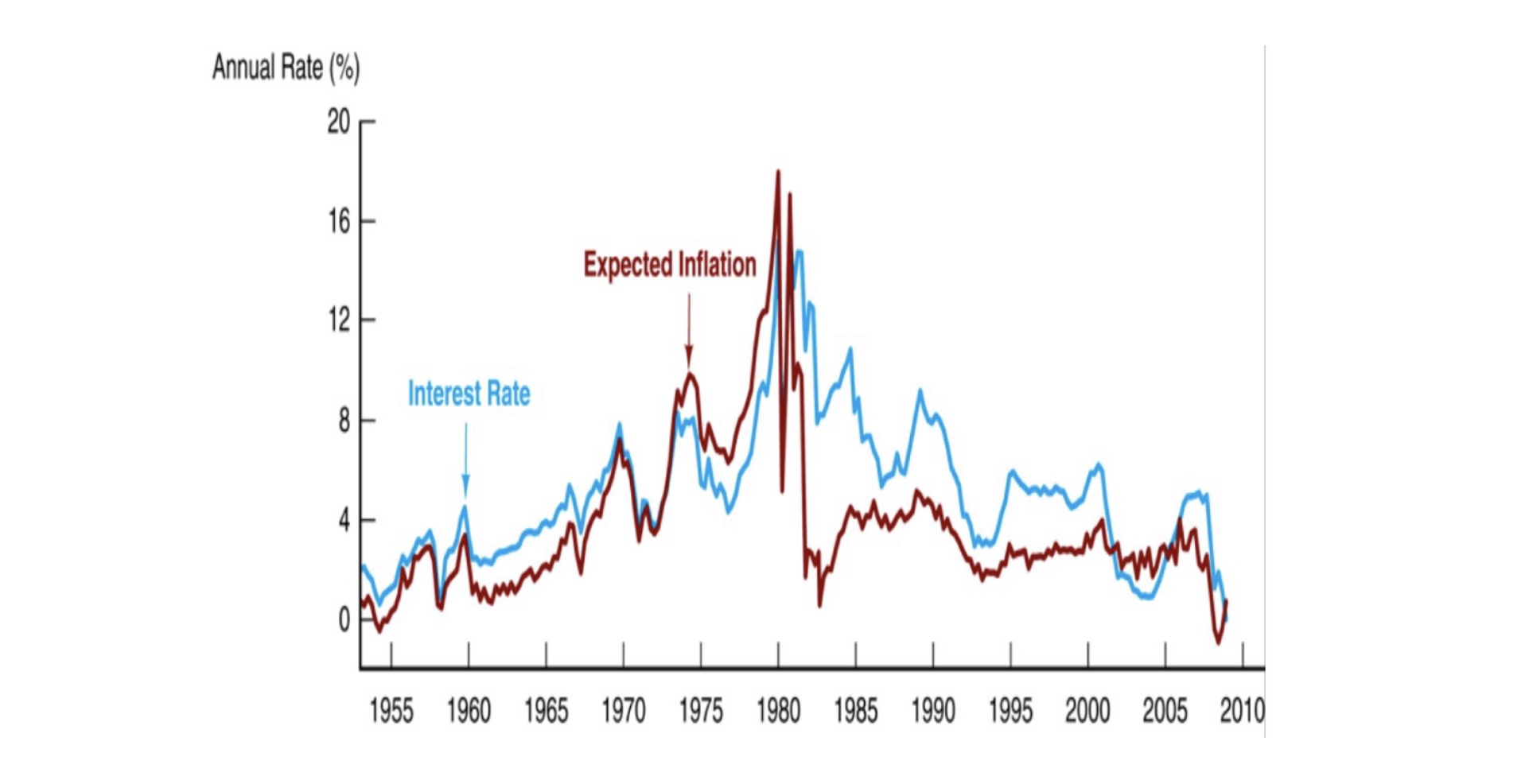
Konjunktur#
in Aufschwungphasen steigen die Zinsen = Angebotseffekt dominiert
Unternehmen wollen mehr Geld
stärker als die veränderte Situation der Haushalte
höhere Zinsen
Quantitative Easing#
Die Anleihekaufprogramme der EZB , bspw PEPP (Pandemic Emergency Purchase Programm) pumpen viel Geld in den Anleihemarkt
steigert den Preis der Anleihen (meist Staatsanleihen)
ceteribus paribus senkt die Zinsen
Kalkül:
kurzfristige Zinssätze lagen schon bei 0%
weitere Lockerung geht nur so
reduziert Spread zwischen Zinsen für verschiedene europ. Staaten
Übung#
Der Anleihemarkt mit Bondangebot \(B^{supply}\) und Nachfrage \(N\)
auf Nachfrageseite mögliche Szenarien
Situation |
Nachfrage |
Preis |
|---|---|---|
Vermögen steigt |
\(N \to\) |
\(P \uparrow\) |
erwartete Rendite sinkt |
\(N \gets\) |
\(P \downarrow\) |
Inflationserwartung steigt |
\(N \gets\) |
\(P \downarrow\) |
Risiko steigt |
\(N \gets\) |
\(P \downarrow\) |
relative Liquidität steigt (zu andern Anleihen) |
\(N \to\) |
\(P \uparrow\) |
Zinsen im Aufschwung:
Nachfrage nach Geld auf Unternehmensseite steigt
mehr Anleihen werden angeboten
Preis steigt => Zinsen steigen
Die Nachfrage nach Bonds kommt erst langsam hinterher
Anstieg der Erwarteten Inflation:
reale Finanzierungskosten sinken: \(B^{supply} \to\)
Erwartete Renditen sinken führt zu \(N \gets\)
Letztendlich: Preise sinken (doppelt)