27.04.2022 Kurz- und Langfristiges Angebot#

Kostenkurve#

Zusammensetzung aus fixen und variablen Kosten: \(C = C_V+C_F\)

Beispielhafte Kostenfunktion:

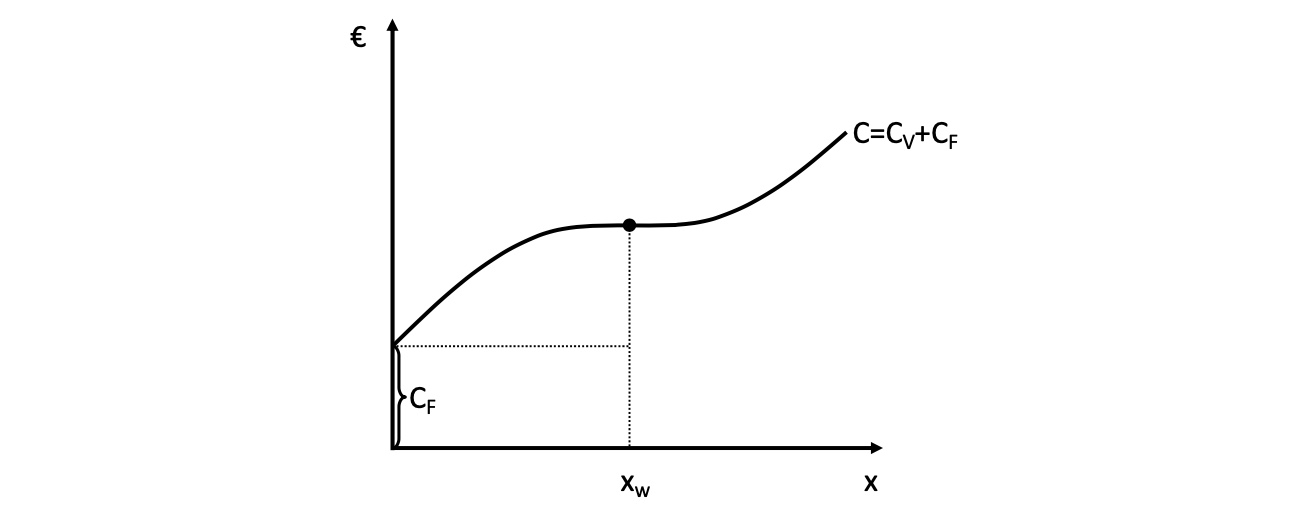
2022-04-27_16.56.05

daraus -> Durchschnittskosten / Einheit = \(\frac{C}{x} = \frac{C_v}{x} + \frac{C_F}{x}\)

  • \(\frac{C}{x}\) = Average Total Cost

  • \(\frac{C_V}{x}\) = Average Variable Cost

  • \(\frac{C_F}{x}\) = average Fixed Cost

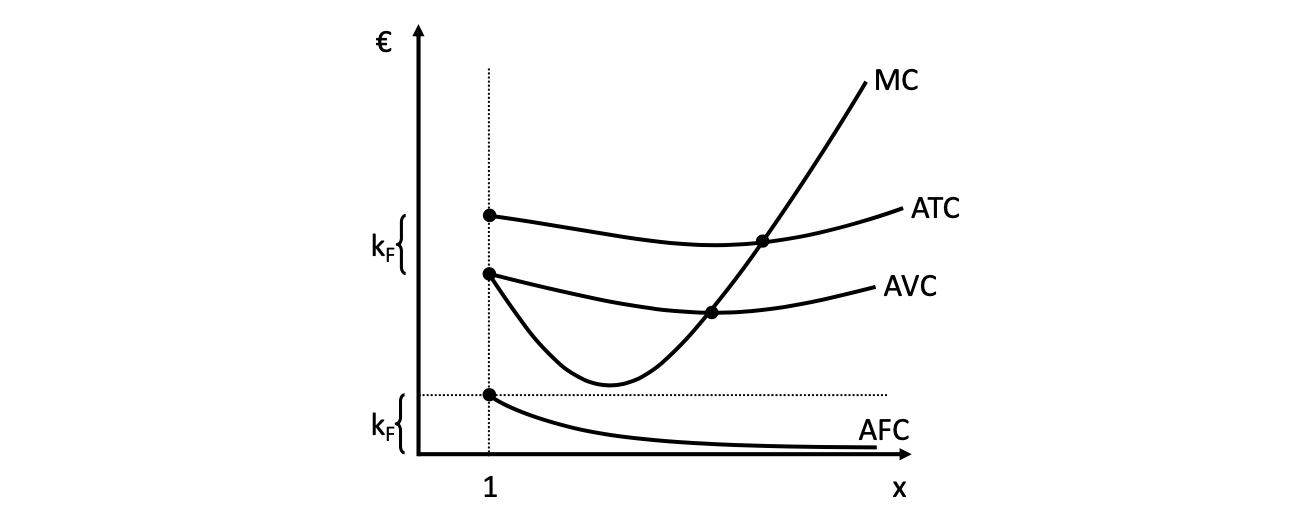
2022-04-27_17.01.30

  • AFC und AVC = ATC-Kurve

  • Minimum der AVC = links von Minimum der ATC

  • wo MC < ATC hat letztere negative Steigung

  • MC schneider AVC und ATC an deren Minimum (denknotwendig!)

Beispielhafte math. Betrachtung: (bei kubischer Gleichung) $\( \begin{aligned} C &= ax^3 - bx^2 + cx + C_F \\ ATC &= \frac{C}{x} \to ax^2 - bx+c+\frac{C_F}{x} \\ AVC &= \frac{C_V}{x} \to ax^2 - bx+c \\ MC &= \frac{dC}{dx} \to 3ax^2 - 2bx + c \end{aligned} \)$

Gewinnkalkül#

aus letzter Woche!

Gewinn = Erlös - Kosten: \(G(x) = E(x) - C(x)\)

  • Maximum bei \(\frac{\partial G}{\partial x} = \frac{\partial E}{\partial x} - \frac{\partial C}{\partial x} = 0\)

  • Grenzgewinn ist null und Grenzerlöse = Grenzkosten

nach Einsetzen der Erlösfunktion \(p = \frac{\partial C}{\partial x}\)

  • Preis für Gut = Grenzkosten = optimal

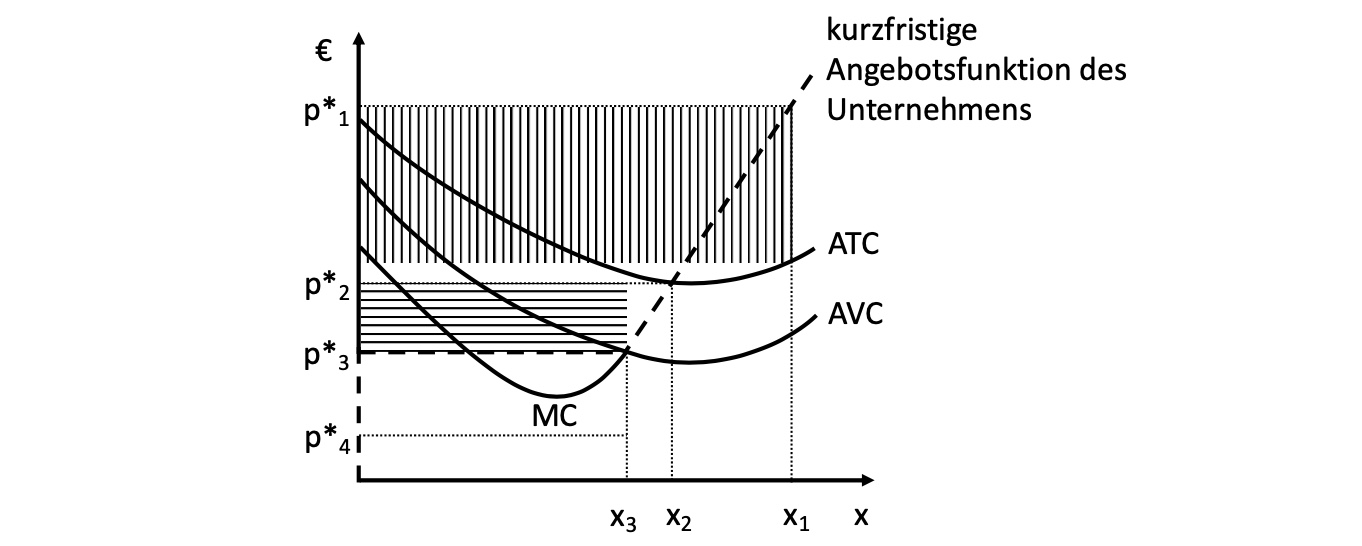
Preisakzeptanz eines Unternehmens kurzfristig

2022-04-27_20.02.36

Preis

Angebot

Gewinn

\(p^* \ge p^*2\)

gemäß MC-Kurve

positiver Gewinn => Champus und Kaviar

\(p^*_2 \ge p^* \ge p^*_3\)

gemäß MC-Kurve

kurzfristig Verluste

\(p^* \le p^*3\)

Einstellung

Fixkosten sind verloren

  • merke: kurzfristig sind Unternehmen bereit, Verluste bis Fixkosten hinzunehmen

    • also Preis zwischen ATC und AVC

langfristig:

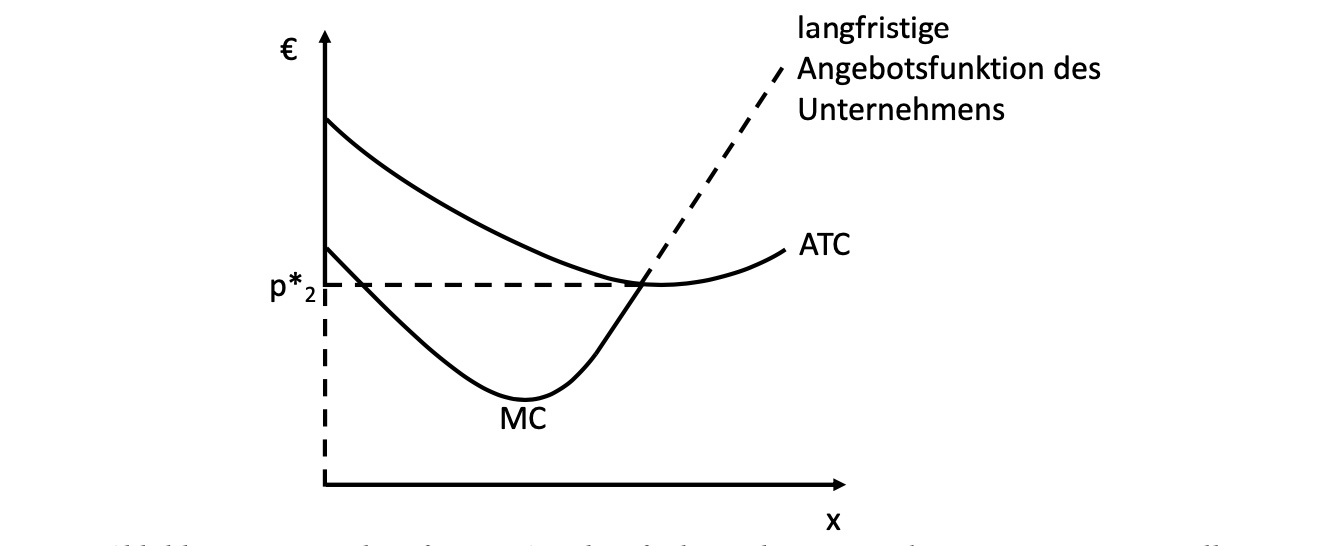
2022-04-27_19.20.25

Marktangebot#

Kurzfristig#

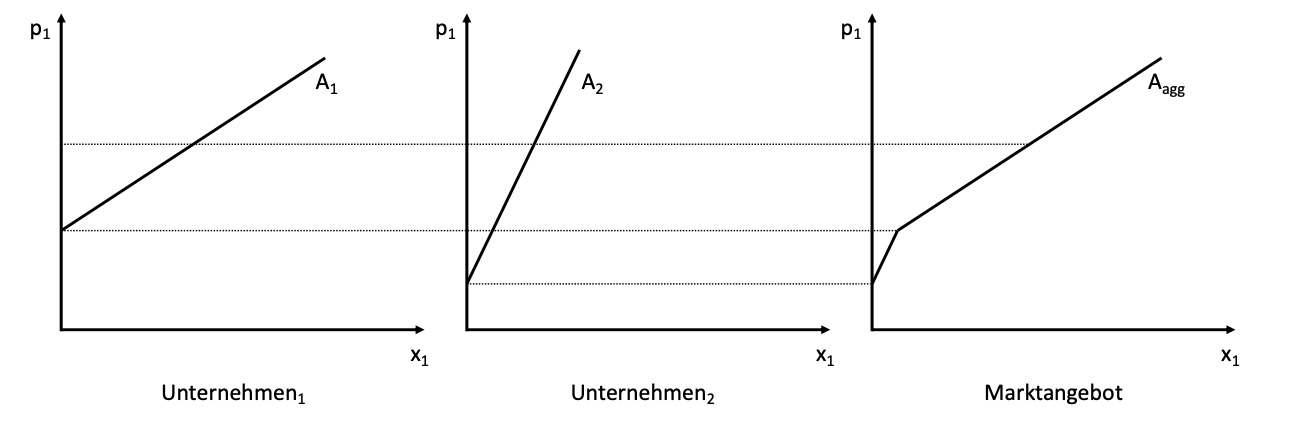
2022-04-27_20.15.24

  • kein Markteintritt / Austritt möglich (konstante Firmenanzahl)

  • Annahme perfekten Wettbewerbs

  • steigende Preise -> steigende Produktion aufgrund steigender Grenzkosten

Langfristig#

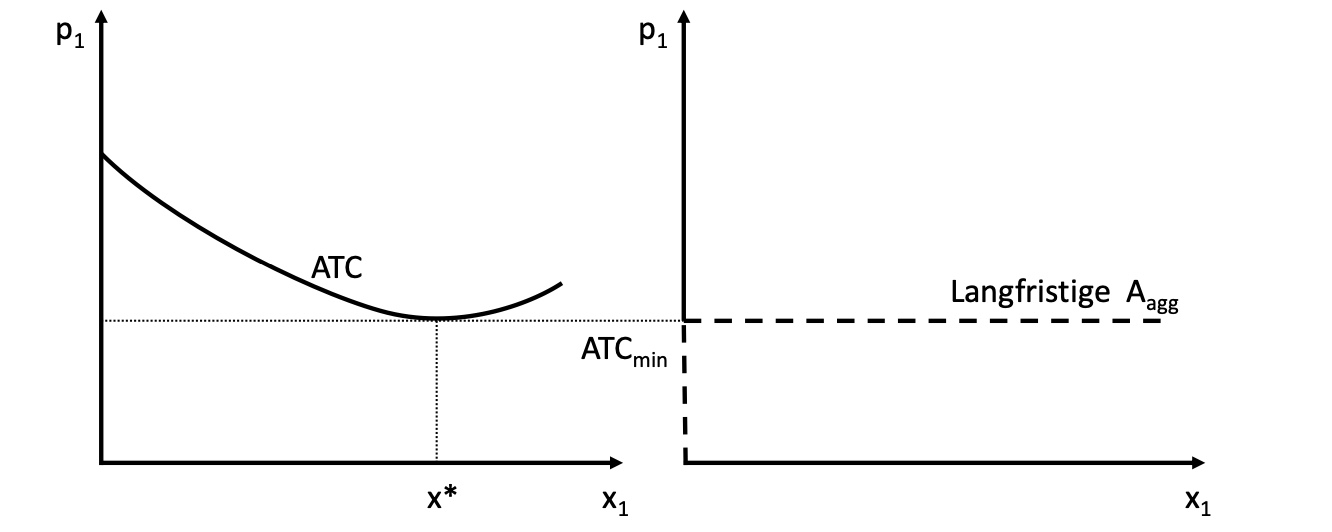
2022-04-27_20.17.13

  • Gewinne und Verluste führen zu Markteintritt / Austritt

    • Gewinn langfristig 0

  • Annahme konstanter Skalenerträge

    • keine Economies of Scale

Produzentenrente#

analog zu Konsumentenrente

Produzentenrente: Summe der Erlöse, die die Grenzkosten der Unternehmen übersteigt

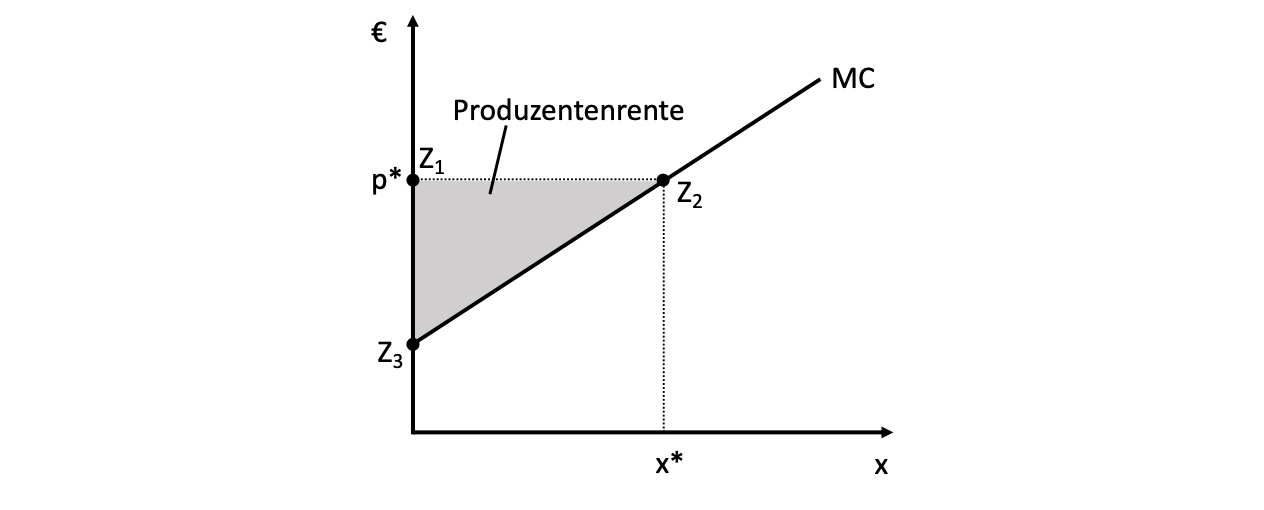
2022-04-27_20.27.31

unterscheidet sich kurzfristig und langfristig (geringer)

Angebotselastizität#

analog zu Nachfrageelastizität: $\( \epsilon_{x,p} = \frac{\Delta x \%}{\Delta p \%} = \frac{ \frac{\Delta x}{x} }{\frac{\Delta p}{p}} \)$

  • langfristiges Angebot ist immer elastischer als kurzfristiges

  • aufgrund Anpassungsreaktionen der Unternehmen

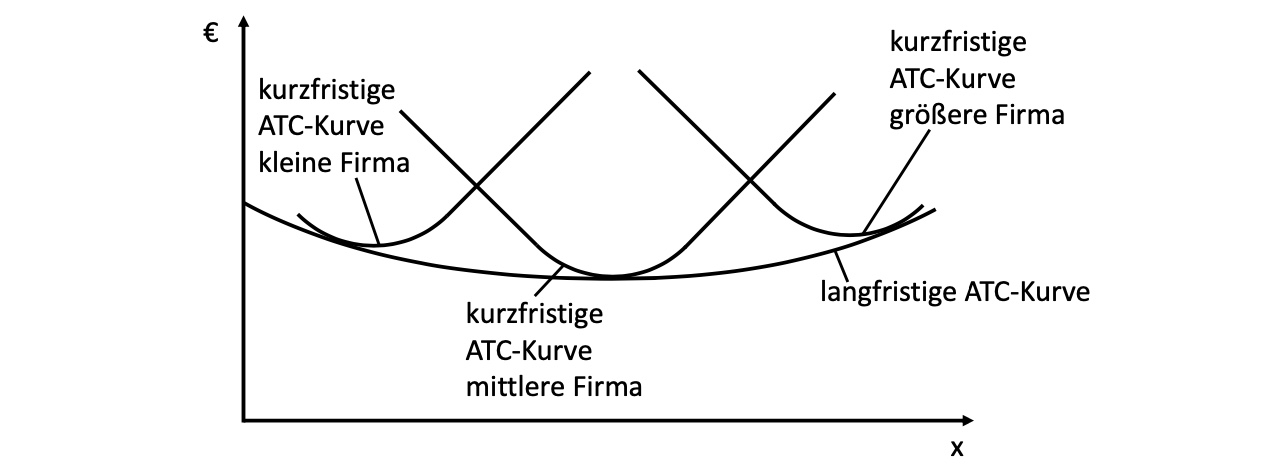
2022-04-27_20.39.48

Übung#

1: Kostenfunktionen#

\(C = x^2 +x +4\)

Berechnung:

  • \(C_V =x^2+x\) (durch Ablesen)

  • \(C_F=4\) (durch Ablesen)

  • \(ATC = \frac{C}{x} = x+1+\frac{4}{x}\)

  • \(AVC = \frac{C_V}{x} = x+1\)

  • \(AFC = \frac{C_F}{x} = \frac{4}{x}\)

Minima der ATC: $\( ATC = x+1+\frac{4}{x} \\ \frac{\partial ATC}{\partial x} = 1+(-1)*\frac{4}{x^2} = 0 \\ \to \frac{-4}{x^2} = -1 \to 4=x^2 \\ \to \bold{x=2 \text{ bei } ATC=5} \)\( Minima der AVC \)\( \frac{\partial AVC}{\partial x} = 2x+1 \\ \text{lineare Funktion: Minimum bei \bf{0,1}} \)\( Grenzkosten: \)\( MC = \frac{\partial C}{\partial x} = 2x+1 \)$ graphische Darstellung: 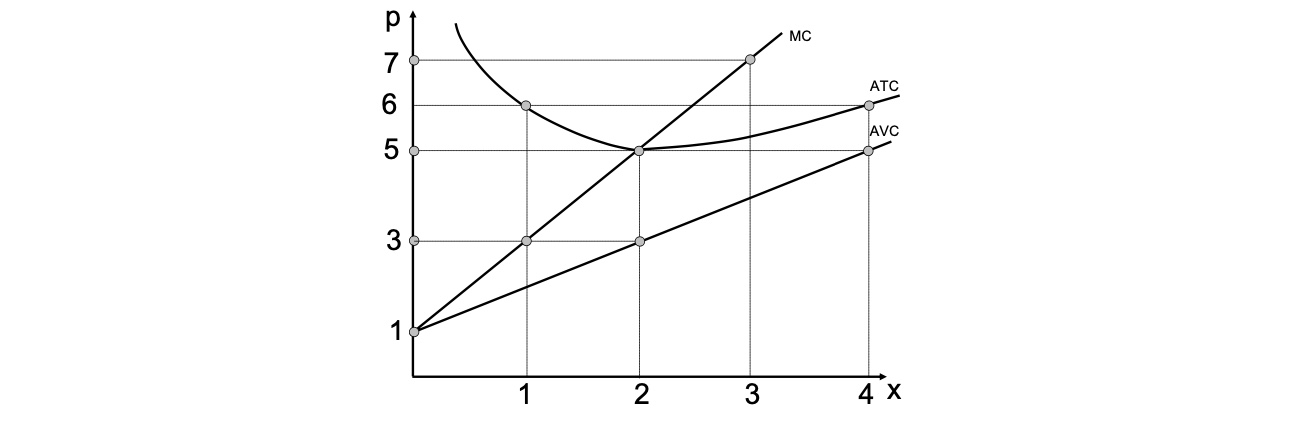2022-05-12_12.35.17

2: Gewinnmaximierung#

Herleitung der Gewinnmaximierungsbedingung MC = p $\( G = E -C = p*x- C\\ \text{Gewinnmaximum bei } \frac{\partial G}{\partial x} = \underbrace{\frac{\partial E}{\partial x}}_p - \underbrace{\frac{\partial C}{\partial x}}_{MC} \\ \implies\frac{\partial G}{\partial x} = p-MC = 0 \\ \to \bold{MC = p} \)\( mit gegebener Kostenfunktion optimale Menge zu Preisniveaus = *{3,5,7}* \)\( p = 3 \to MC = 3 = 2x+1 \to 2x = 2 \implies \bold{x=1} \\ p = 5 \to MC = 5 = 2x+1 \to 2x = 4 \implies \bold{x=2} \\ p = 7 \to MC = 7 = 2x+1 \to 2x = 6 \implies \bold{x=3} \\ \)\( und dazugehöriger Gewinn: \)G = p*x- (x^2+x+4)\( \)\( p = 3 \to 3*1 - (1^2+1+4) = \bold{-3} \\ p = 5 \to 5*2 - (2^2+2+4) = \bold{0} \\ p = 7 \to 7*3 - (3^2+3+4) = \bold{5} \)$

3: kurz-und Langfrist#

  • Kurzfristig: Anbieten bei MC=p und \(p \ge AVC_{min}\)

  • Langfristig: Anbieten bei MC=p und \(p \ge ATC_{min}\)

Graphisch: 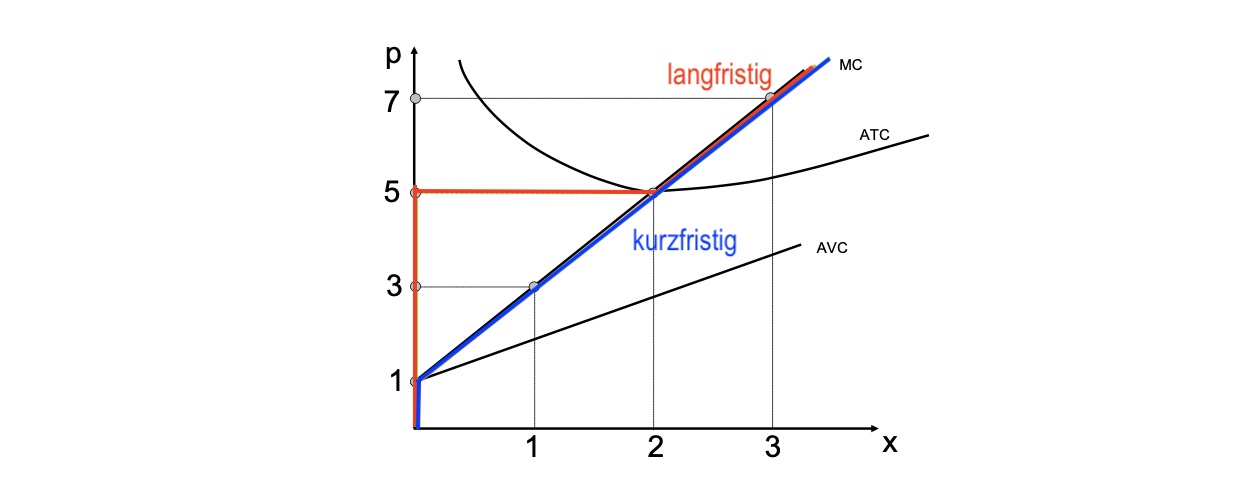2022-05-12_13.00.42

4: Martkangebot (kurzfristig)#

was passiert bei zwei identischen Unternehmen mit der gegebenen Kostenfunktion:

  • in Kurzfrist bieten beide bei \(MC = p = 2x+1\) an

  • für Horizontaladdition: nach x umstellen!

    • Unternehmen 1: \(S_1 = 2x_1 + 1 \to x_1 = \frac{1}{2}p-\frac{1}{2}\)

    • Unternehmen 2: \(S_2 = 2x_2 + 1 \to x_2 = \frac{1}{2}p-\frac{1}{2}\)

  • Addieren: \(x_m = x_1+x_2 = \frac{1}{2}p-\frac{1}{2} + \frac{1}{2}p-\frac{1}{2} = \bold{p-1}\)

  • Zurückumstellen: \(p = x_m +1\)

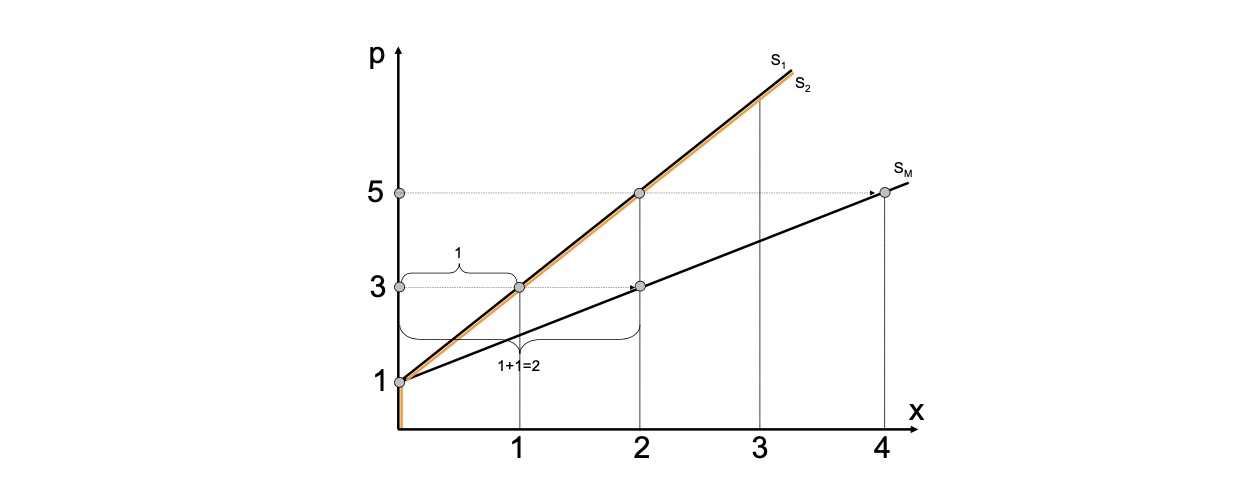
2022-05-12_13.13.36

merke: Marktangebotsfunktion ist immer flacher als individuelle!

  • neue Anbieter = Drehung der Angebotsfunktion

    • flacheres Angebot = Preis sinkt

5: Marktangebot (langfristig)#

langfristiges Angebot gilt: \(p = ATC_{min}\)

  • beim minimum der ATC wird angeboten, darunter nicht

  • wenn der Preis kurzfristig drüber liegt = Neueintritte

    • langrfristig dann kein Gewinn mehr

6: Prognose kurz/langfrist#

  • 2 Unternehmen mit bekannter identischer Kostenfunktion

  • langfristiges Angebot \(p = 5\)

  • Nachfragefunktion \(p = -x+9\)

Gleichgewicht in Langer Frist: Angebot = Nachfrage \(5 = x-9 \to \bold{x= 4}\)

  • Unternehmen bei p=5 bieten an \(x = 2\)

  • Markt hat langfristig also nur 2 Unternehmen haltbar

Einkommenschock der Nachfrage auf \(p = -x+13\)

  • kurzfristiges Angebot \(p = x +1\), Gleichsetzen => x = 6; p= 7

  • Langfristiges Angebot \( p = 5\), Gleichsetzen => \(x = 8, p= 5\)

    • 4 Unternehmen langfristig haltbar

2022-05-12_13.41.13