07.11.2022 Hicksche Nachfragefunktion#

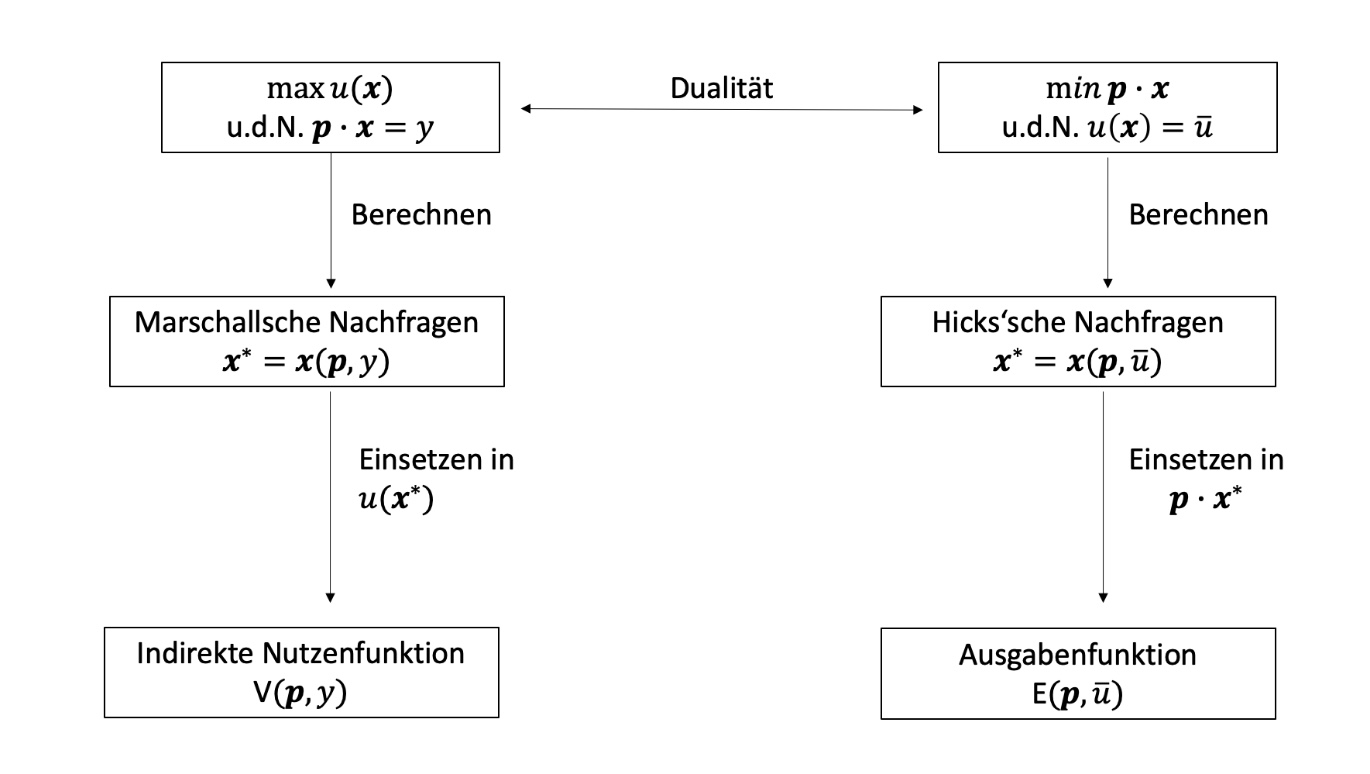
Ausgabefunktion#

Dualität der Axiome

graph TD Consumer --> a[Max U von x,y] & b[Min px+py] a --> c[Marshallshe Nachfrage] b--> d[Hicksche Nachrafage]

Hicksian Demand: Minimiere Kosten von gegebenem Nutzenniveau

Marshallan Demand: Maximiere Nutzen bei gegebenem Preis

Lösung des Hickschen Problems ergibt \(x^*,y^*\) (als Funkltion von \(p_x,p_y,u\)) und Einsetzen in Kostenfunktion liefert Ausgabenfunktion

Nutzenmaximierung

Kostenminimierung

\(Max \ U(x,y) \ s.t. \ p_x x+ p_y y \le I\)

\(Min \ p_x x+ p_y y \ s.t. U(x,y) \ge u^*\)

img

img

Bedingung beides gleich: MRS = MRT

Lösung des Optimierungsproblems#

Annahme: \(U(x,y) = x^{1/2} y^{1/2}\)

\[\begin{split} \text{Min } \ p_x x+ p_y y \ \text{ s.t. } U(x,y) \ge u^* \\ L = p_x x+p_y y + \lambda (U_p- x^{1/2} y^{1/2}) \end{split}\]

Ableitung

\[\begin{split} \begin{aligned} I.\frac{\partial L}{\partial x} &= p_x - \lambda \frac{1}{2}x^{-1/2}y^{1/2}= 0\\ II.\frac{\partial L}{\partial x} &= p_y - \lambda \frac{1}{2}y^{-1/2}x^{1/2} = 0\\ III.\frac{\partial L}{\partial \lambda} &= U_p- x^{1/2} y^{1/2} = 0 \end{aligned} \end{split}\]

nach Lambda umformen und I. und II. gleichsetzen

\[ x = \frac{p_y y}{p_x} \]

einsetzen in III.

\[\begin{split} U_{p}= \left( \frac{p_{x}y}{p_{y}} \right)^{1/2} (y^*)^{1/2} \\ \to y^* = \left( \frac{p_{x}}{p_{y}} \right)^{\frac{1}{2}}U_{p} \\ \to x^* = \left( \frac{P_{x}}{P_{y}} \right)^{\frac{1}{2}}U_{p} \end{split}\]

einsetzen in zu minimierende Kosten

\[\begin{split} E(p_x,p_y,U_p) = p_x \cdot \left( \frac{p_{x}}{p_{y}} \right)^{\frac{1}{2}}U_{p} + p_y \cdot \left( \frac{p_{x}}{p_{y}} \right)^{\frac{1}{2}}U_{p} \\ \implies E(p_x,p_y,U_p) = 2p_x^{1/2} p_y^{1/2} U_p \end{split}\]

Dualität der Funktionen#

Zusammenhang zwischen den Funktionen

img

indirekten Nutzenfunktion = Ausgabenfunktion

Wozu Ausgabenfunktion#

  • hier ist Interpretation ordinal (man kann Werte ablesen die was bringen)

  • Nutzenniveau wird in Kosten „übersetzt“ (money metric)

  • erlaubt Policy Bewertung einer Maßnahme

    • durch Kompensationszahlungen vor / nach

Arten der Kompensationszahlungen:

  • CV: Compensating Variation

    • Zahlung als Ausgleich des verlorenen Nutzens

  • EV: Äquivalende Variation

    • wie viel sind wir bereit für Maßnahmenverhinderung zu zahlen

Beispiel: Gaspreis wird erhöht von \(s_0\) auf \(s_1\)

  • dann \(CV = E(s_0,p_a, U_0)- E(x_1,p_a, U_0)\)

    • Zahlung bei unveränderten Anderen Preisen für Ausgleich des verlorenen Nutzens

    • für Kosten-Nutzen-Analysen

    • Ex-post-Perspektive

  • \(EV = E(s_0,p_a,U_1)-E(s_0,p_a,U_0)\)

    • Bereitschaft des Konsumenten, die Erhöhung zu verhindern

    • für Wohlfahrtsverlust von Maßnahmen

    • Ex-ante-Perspektive

das ist besser als Konsumenten preislich direkt zu entlasten, da dass zu Überkompensation führt

Carte-Blanche–Prinzip#

zu deutsch: Blankoscheck

Aus dem mikroökonomischen Ansatz folgt, dass Geld geben immer besser ist als Güter geben!

  • freie moneätre Transferzahlung schwach gegenüber anderen Leistungen vorgezogen

  • in Realität: zweckgebundene Zahlungen (Wohngeld, …)

empirisch aber: ungebundene Transferzahlungen sind besser und werden nicht verschwendet

Übung#

Zusammenhang zwischen beiden Funktionen!

img