05.04.2022 Einfuehrung#
induktive Statistik:
aus Stichprobe Aussagen über eine Grundgesamtheit schließen
Grundlage = Wahrscheinlichkeit
Zufallsexperiment: wohldefinierter Vorgang ohne feststehendes Resultat
mit Ergebnisse \(\{ w_{1}, w_{2},... \} = \Omega\) Ergebnismenge
Ereignis = eine Teilmenge der Ergebnismenge \(A \subseteq \Omega\)
Elementarereignis: Eregnis mit einem Ergebnis \(\{w_{1}\}\)
Wahrscheinlichkeit#
Ereignis \(A \subseteq \Omega\)
Funktion P: \(A \to P(A)\) = Wahrscheinlichkeitsabbildung
kolmogoroffsche Axiome
\(P(A) \ge 0\)
\(P(\Omega) = 1\)
wenn \(A \cap B = \emptyset\) dann \(P(A \cup B) = P(A) + P(B)\)
Laplace Wahrscheinlichkeiten:
alle Elementarereignisse gleich wahrscheinlich
Eregnis A hat m Elementarereignisse
=> \(P(A) = \frac{m}{n}\)
Mengen#
Mengenoperationen#
Schnittmenge \(A \cap B\)
Vereinigungsmenge \(A \cup B\)
Differenzmenge \(A \setminus B\)
Komplementärmenge \(A^{C}\)
Beispiel im Casino mit Falschspielern F und Trickstern T und Darstellung mit Venn
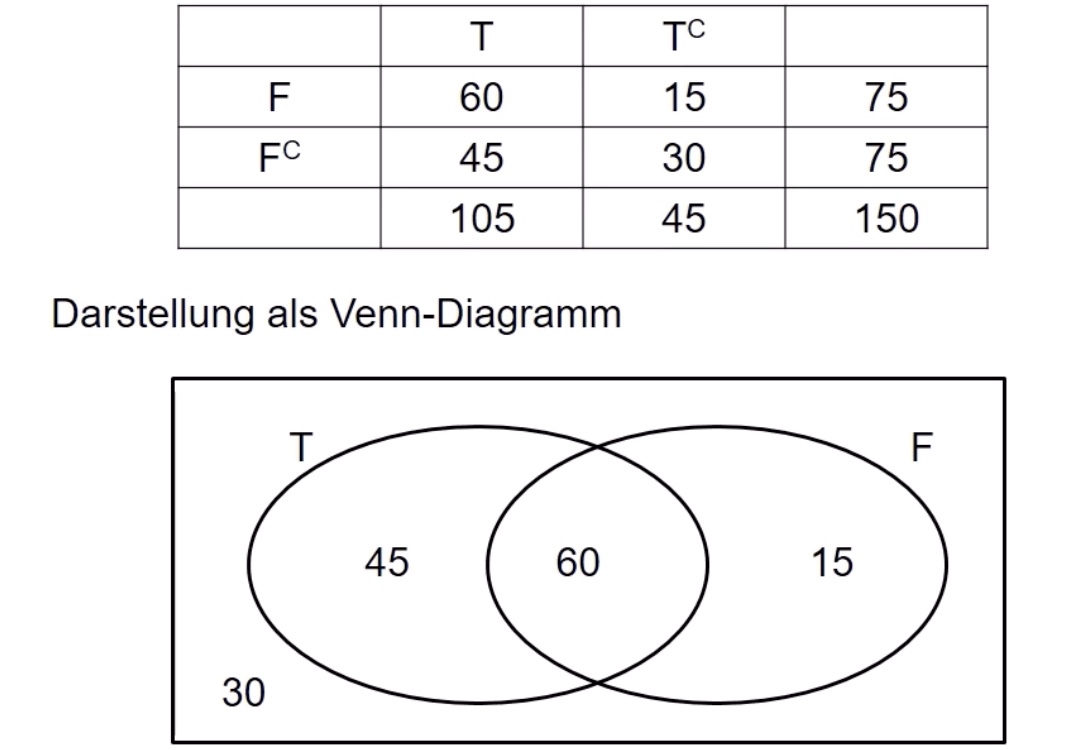
Rechenregeln#
kommutativ: \(A \cap B = B \cap A\)
assoziativ: \((A \cap B) \cap C = A \cap (B \cap C)\)
distributiv: \((A \cap B) \cup C = (A \cup C) \cap (A \cup B)\)
de Morgan:
\((A \cap B)^{C}= A^{C} \cup B^{C}\)
\(A \subseteq B \to B^{C} \subseteq A^{C}\)