09.11.2022 Erweiterungen des Solow-Modells

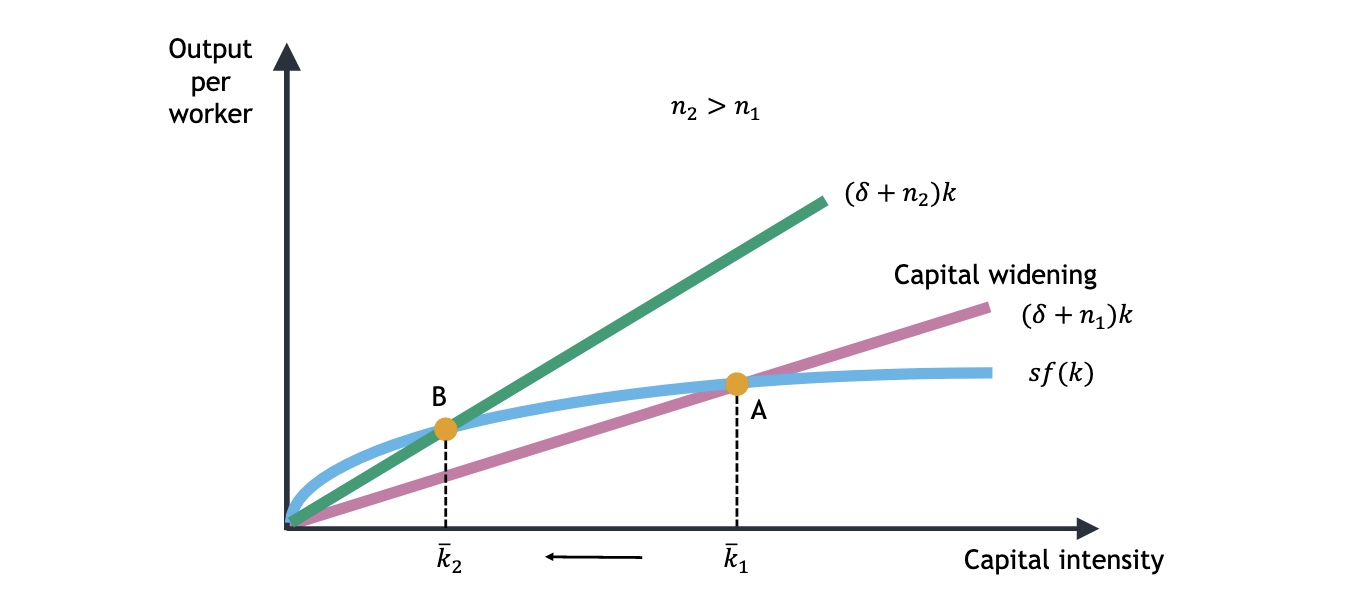
Bevölkerungswachstum

das Wachstum führt zu geringerem Kapitalstock pro Arbeiter (niedrigere \(\bar{k}\)) $\( sf(k) = (\delta +n) k \)$ => früherer Steady-State Punkt

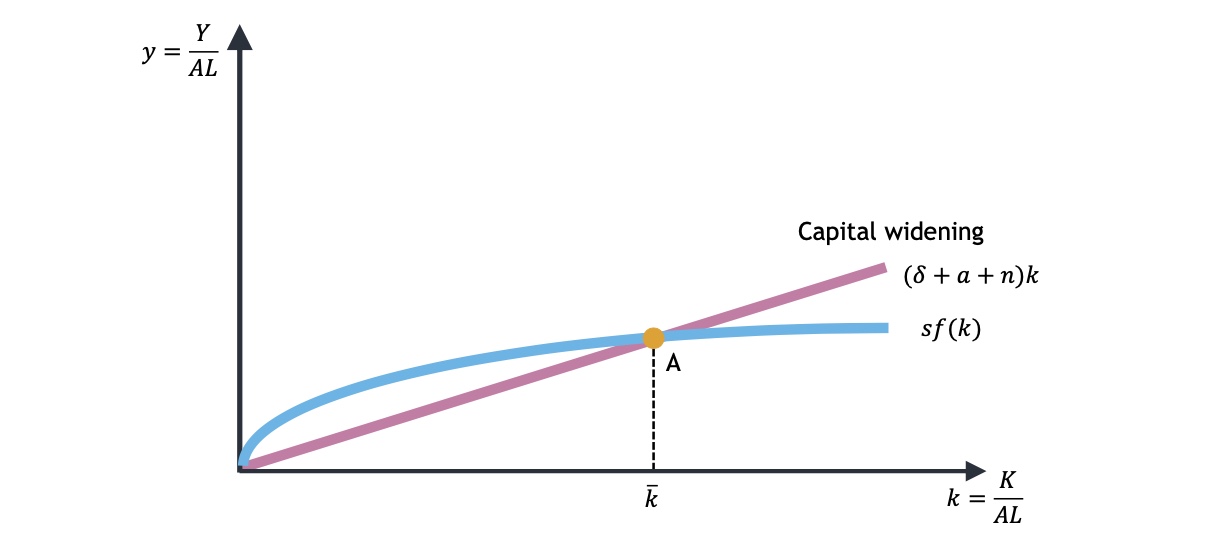
Technologischer Fortschritt

= feste Menge Arbeit und Kapital mehr Output \(Y = F(A,K,L)\)

• von Interesse insbesondere arbeitssparender Fortschritt

  • labor augmenting technological progress

  • Wachstumsrate von A = a

  • \(Y = F(K, A \times L)\)

dann Anpassung der Einheiten pro. P $\( y = \frac{Y}{A \times L}\\ k = \frac{K}{A \times L} \\ \Delta k = s \times f(k)- (\delta+n+a) \times k \)$

• je höher Technologischer Fortschritt = schnellere Abschreibung alterer Maschinen (eigene Erklärung)

• deswegen \((\delta+n+a) \times k\)

Wachstum im Steady State:

Art	Wachstum
\(y,k\)	0
\(Y/L, K/L\)	a
\(Y, K\)	a+n

Wachstumszerlegung

Technologieniveau niemals bekannt, aber rückwarts ausrechenbar

aus \(Y = (A,K,L)\) da Y bekannt ist => Solow Residuum / TFP (Total Factor Productivity)

Solow Residuum: der Faktor, der nicht durch Veränderung in Sparquote / Kapitalstock / Bevölkerungswachstum erklärt werden kann = „measure of our ignorance“

das was Solow nicht erklären kann (institutionelle Faktoren etc), wird in einem Indikator zusammengefasst

=> macht Großteil des Wachstums aus => Solow Modell ist whack

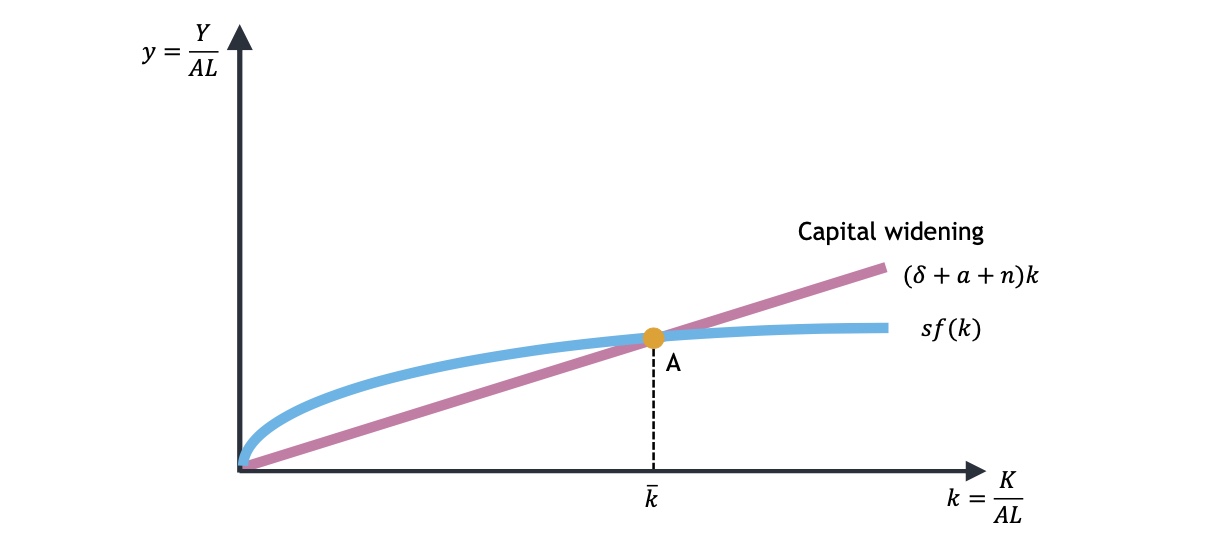
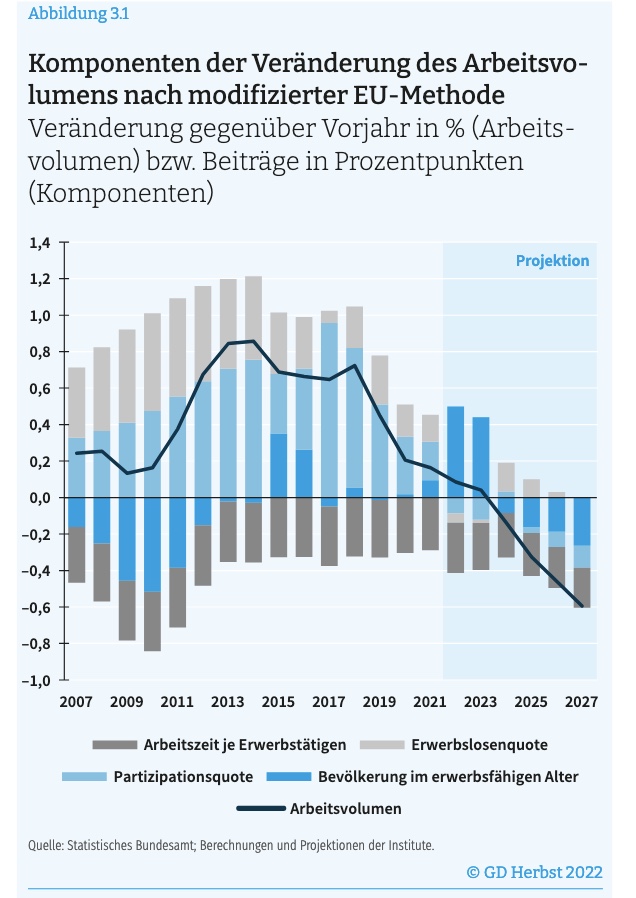
Empirie

Faktoren bei Arbeitsvolumen:

• Arbeitszeit Durchschnitt

• Partizipationsquote

• Beölkerung erwerbsfähiges Alter

• Erwerbslosenquote

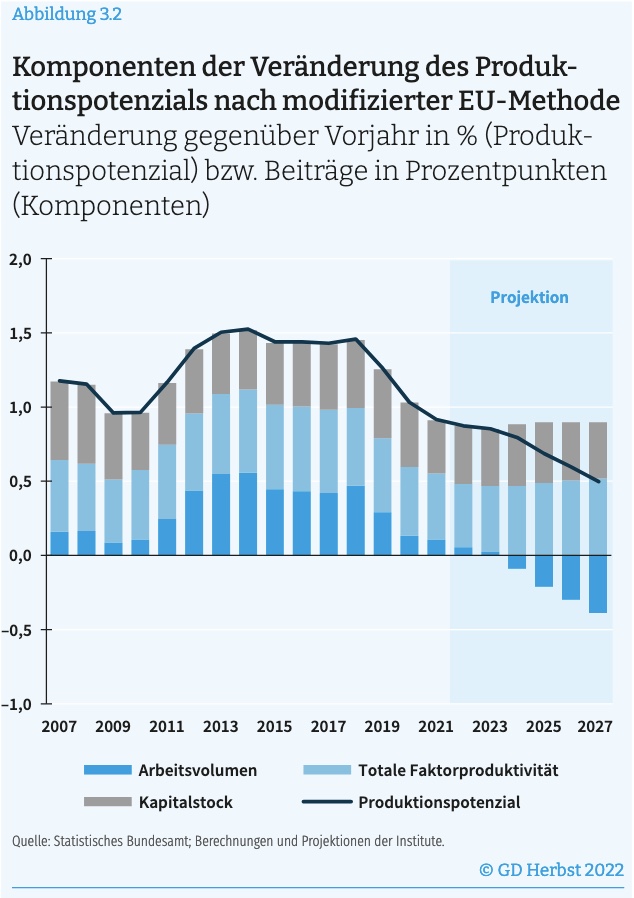
in EU: insbesondere TFP spielt starke Rolle

Arbeitsvolumen	Wachstum EU

Weitere Befunde zu Demographie:

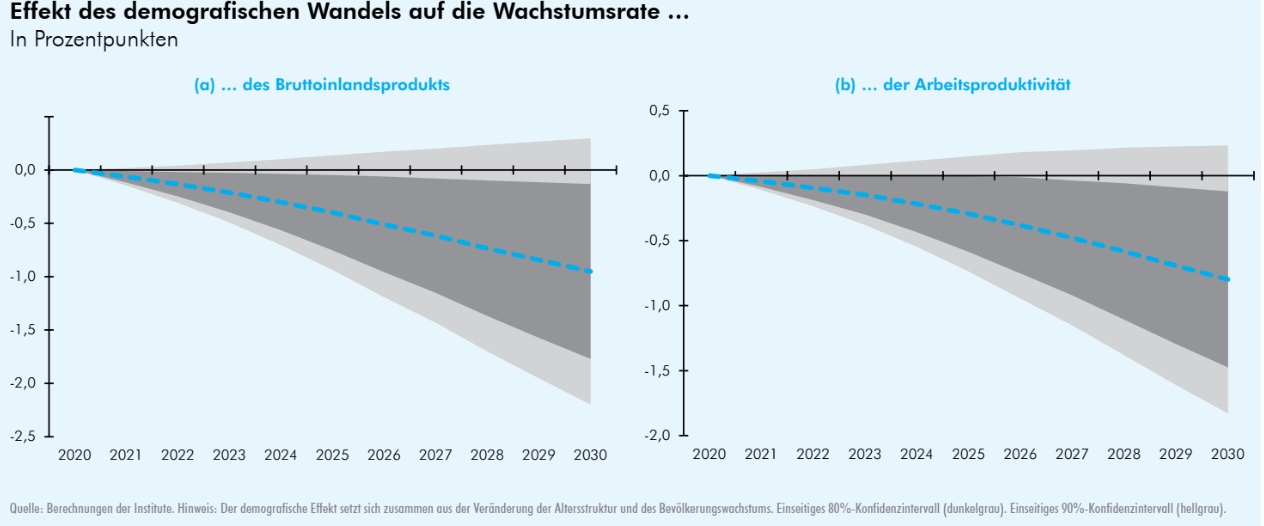
Übung

Solow mit Erweiterung:

• Bevölkerungswachstum: \(L_{t+1} = (1+n)L_t\)

• Technolgiewachstum: \(A_{t+1} = (1+a)A_t\)

• \(Y= F(K,AL)\)

dann Einheiten effektiver Arbeit: \(\hat{y} = \frac{Y}{AL}\)

kapitalintensität (effektiv) : \(\hat{k} = \frac{K}{AL}\)

Kapitalakkumulation: \(\Delta k = sy- (\delta+n+a) k\)

• warum n schlecht: höhere Bevölkerung -> niedrigere Kapital pro Kopf

• warum a (technologischer Fortschritt) schlecht: jeder Arbeiter braucht mehr Kapital

neue Gleichgewichtsbedingung: \(\underbrace{sy}_{Investitionen} = \underbrace{(\delta+n+a)k}_{Kapitalverbrauch}\)

\(\hat{y} = \frac{Y}{AL}\)

• wenn \(\hat{y}\) konstant

• dann muss Y, K mit technologischen Fortschritt (a) und Bevölkerungswachstum (n) wachsen

• und pro-Kopf BIP nur mit technologischem Forschritt (a)

---

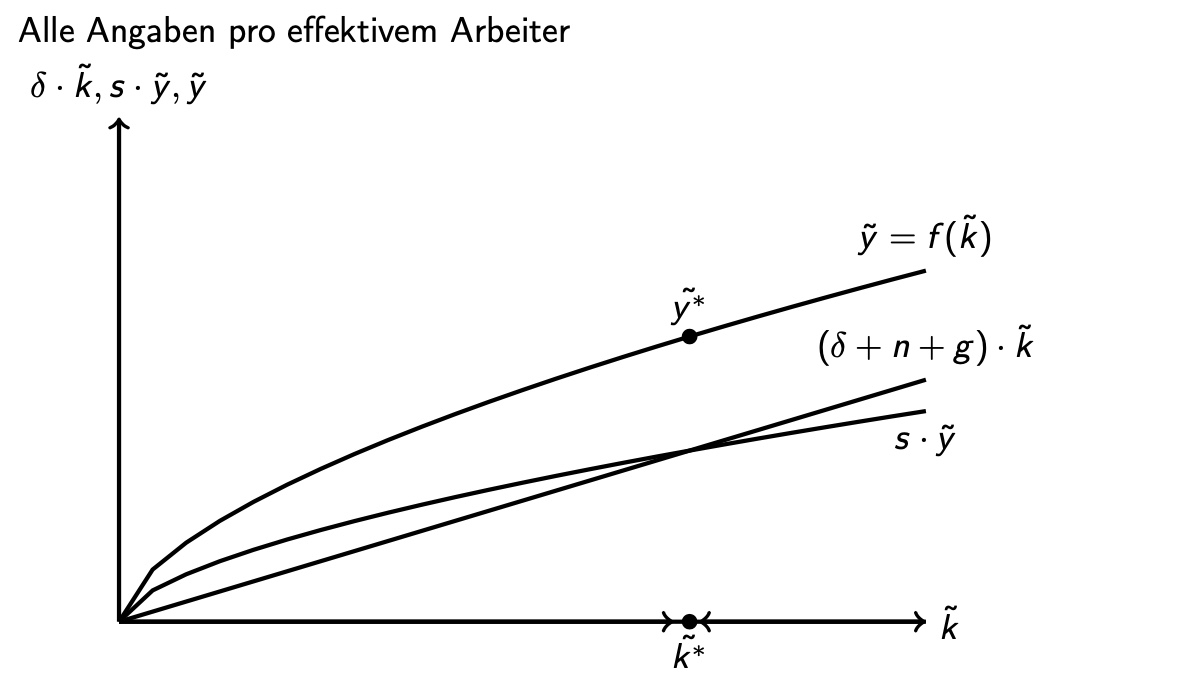
Sparquote der goldenen Regel

Gleichgewicht, an dem Konsum maximal ist!

Annahmen

• Sparquote kann beinflusst werden (endogen)

• Indivuuen wollen Konsum => Nutzenmaximierung

Warum?:

• zu hohe Sparen = hohe Investitionen

  • steigender Kapitalstock

  • viele Abshreibungen, die ausgeglichen werden müssen

  • senkt Konsummöglichkeiten

• zu niedriges Sparen

  • zu geringes Wachstum

  • weniger Konsum

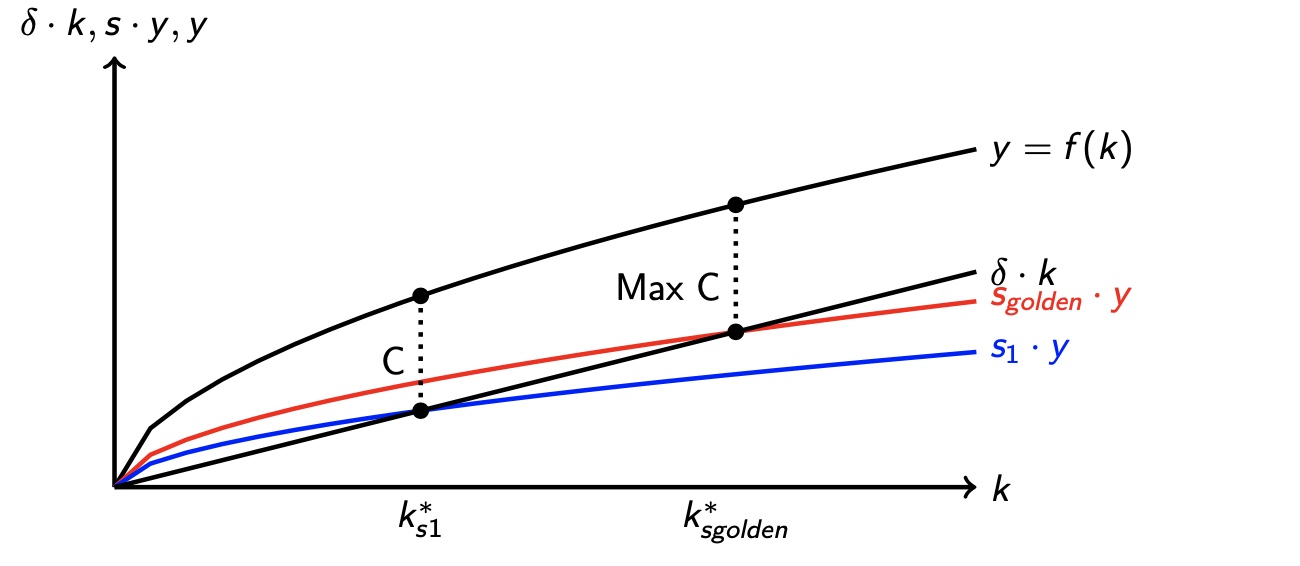
Mathematisch: \(f'(k) = \delta \implies MPK\)

• Steigung der Produktionsfunktion y gleich

• Steigung der Kapitalakkumulationsgeraden

Schritte:

1. f(k) zeichnen

2. dk verschieben bis f(k)

3. dann Schnittpunkt, an dem Steigungen tangential

4. senkrechten Strich nach unten = Punkt der goldenen Regel

5. daraus dann goldene Sparquote entnehmen

Situationen:

• \(s > s_g\) = dynamisch ineffizienter Bereich

• \(s < s_g\) = dynamisch effizienter Bereich

Rechnung:

• Produktiosnfunktion \(Y = K^{0.5}L^{0.5}\)

• s = 0.24

• d = 0.06

\[ y = \frac{Y}{L} = K^{0.5}L^{-0.5} = \Big(\underbrace{\frac{K}{L}}_k\Big)^{0.5} = k^{0.5} \]

Also: \(y = k^{0.5}\) $\( sk^{0.5} = \delta k \to k^{0.5}=\frac{s}{\delta} \to k=(\frac{s}{\delta})^2 \)\( einsetzen \)\( k = (\frac{s}{\delta})^2 = (\frac{0.24}{0.06})^2 = 16 \\ y = k^{0.5} = \sqrt{16} = 4 \)$

andere Aufgabe:

• \(y = k^{0.5}\)

• s = 0.4

• \(\delta\) = 0.1

ermittle k,C,I im GG $\( \bar{k} = (\frac{s}{\delta})^2 = (\frac{0.4}{0.1})^2 = 16 \\ \bar{y} = 4 \\ \bar{c} = (1-s)y = 0.6 \times 4 = 2.4 \\ Y = C+I \to I = Y-C \\ \to 4-2.6 = 1.4 \)\( Goldene Regel: \)\( f'(k) = \delta \\ 0.5 k^{-0.5} = \delta \\ einsetzen: sk^{0.5} = \delta k\\ \to (0.5 k^{-0.5})k = sk^{0.5} \\ s = 0.5 \)$