07.04.2022 Haushalte

Mikroökonomik

was ist Mikroökonomik?

flowchart TD Datenänderung & Ratenänderung --> M((Modell))

Modelle

• sind realistisch weil hilfreicher Output

• vereinfachen

• gibt verschiedene je nach Problem

Modell der Haushalte

mikroökonomisches Modell des Haushalts: Präferenzen-Restriktionen-Schema

graph TD Präferenzen & Restriktionen --> Handlungen Handlungen --> Ergebnisse Ergebnisse --> 1(intendiert) & 2(nicht intendiert)

durch Änderungen der Restriktionen (Schocks) Änderungen der Ergebnisse interpretieren

Annahmen über Haushalte:

• Einkommenbudget B

• Einkauf von Gütern \(x_{1}, x_{2},...\)

• zu Marktpreisen \(p_{1}, p_{2},...\)

• darus Nutzen / Utility U

• Haushalte sind nutzenmaximierend

Nutzenfunktion

Annahmen über Nutzenfunktion \(U = U(x_1,x_2)\):

• durchgängig positiver Nutzen

• abnehmender Grenznutzen

  • dadurch Kurve konkav

Abbildung Nutzenkurve: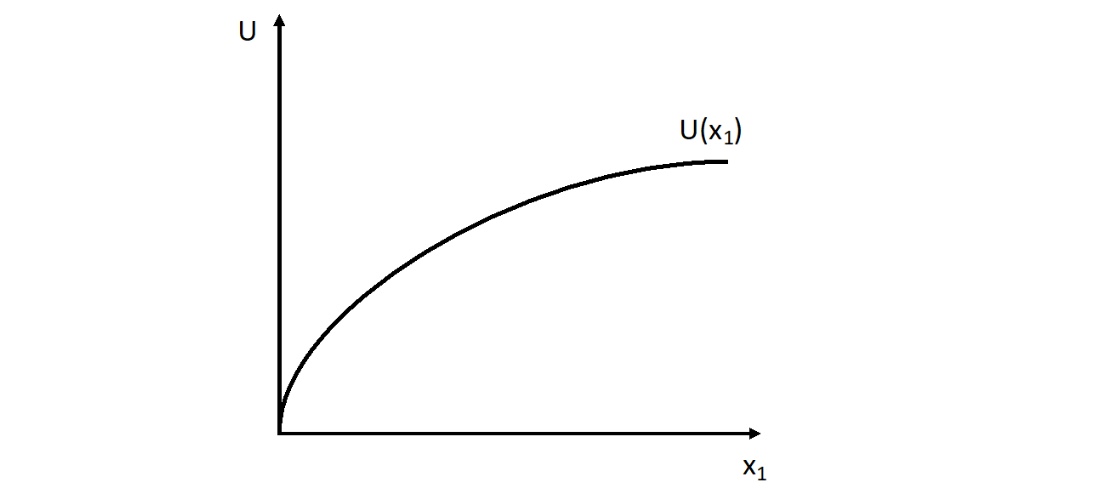

mathematische Betrachtung:

1. Ableitung = Grenznutzen = positiv: \(\frac{\partial U}{\partial x_1} > 0\)

2. Ableitung = Steigung des Grenznutzens = negativ: \(\frac{\partial^2 U}{\partial x_1^2} < 0\)

Indifferenzkurve

Nutzenfunktion erweitert auf Indifferenz zwischen zwei Gütern: $\( d U = \frac{\partial U}{\partial x_1} * d x_1 + \frac{\partial U}{\partial x_2} * d x_2 = 0 \)$

• \(d U\) = absolute Veränderung Nutzen

• \(\frac{\partial U}{\partial x_1} * d x_1\) = Grenznutzenfunktion * Veränderung der Menge \(x_1\)

• \(=0\): unter Annahme konstanten Nutzens

also wie verändert sich die Zusammensetzung der Güter, wenn ich Nutzenniveau konstant halte. 
wenn x1 kleiner, dann x2 zwangsläufig größer etc.

Substitutionsrate

aus dieser Gleichung lässt sich Substitutionsrate herleiten $\( \frac{d x_2}{d x_1} = - \frac{\frac{\partial U}{ \partial x_1}}{\frac{\partial U}{ \partial x_2}} = | MRS | \)$

MRS: Marginal Rate of Substitution: subjektive Substitutionswollen eines Haushalts (wieviel ist er bereit aufzugeben für ein Gut)

Darstellung als Indifferenzkurven

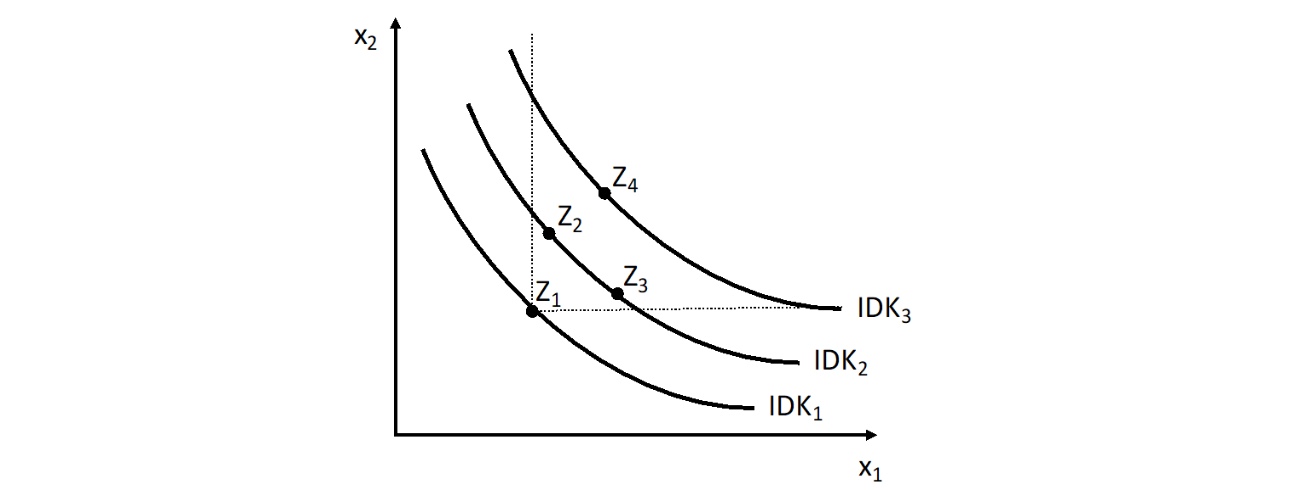
• beschreibt mögliche Güterkombinationen zwischen zwei Gütern

• auf einer Kurve = indiffernt gegenüber Kombination

• unter der Kurve = weniger Nutzen

• Nicht gerade wegen Grenznutzen

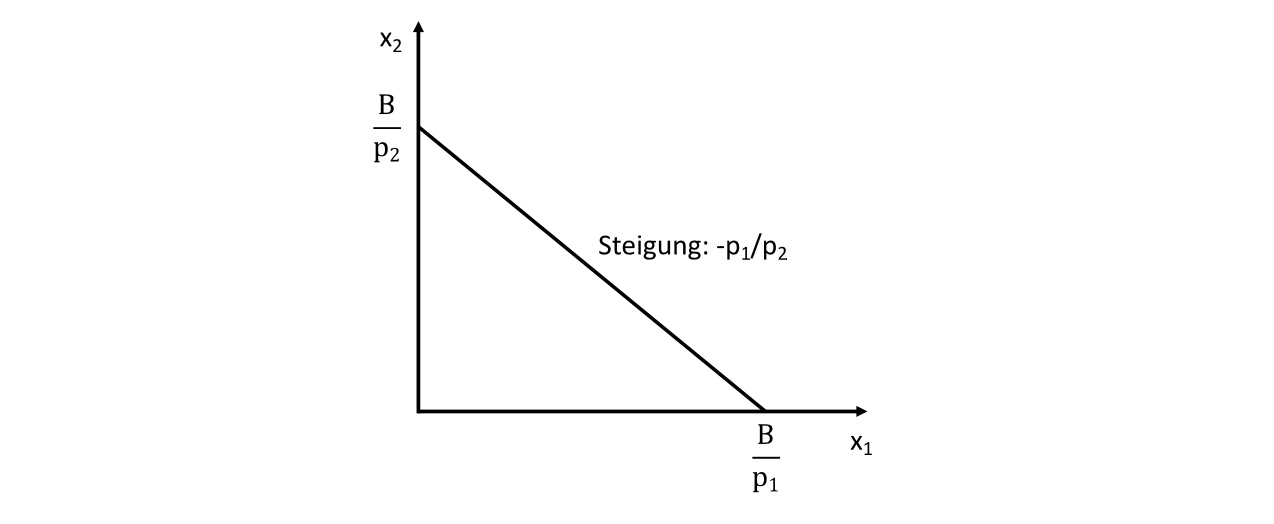
Budgetgerade

Möglichkeitenraum, den ein Haushalt aufgrund seines Budgets hat

Formel: \(B = p_1 x_1 + p_2 x_2 \)

\[\begin{split} \text{Budgetgleichung: } B = p_1 x_1 + p_2 x_2 \\ \text{Steigung: } \frac{d x_2}{d x_1} = - \frac{p_1}{p_2} = | MRT | \end{split}\]

MRT: Marginal Rate of Transformation: objektives Substitutionskönnen des Haushalts über Preise

Haushaltsgleichgewicht

Zusammenfügen beider Kurven

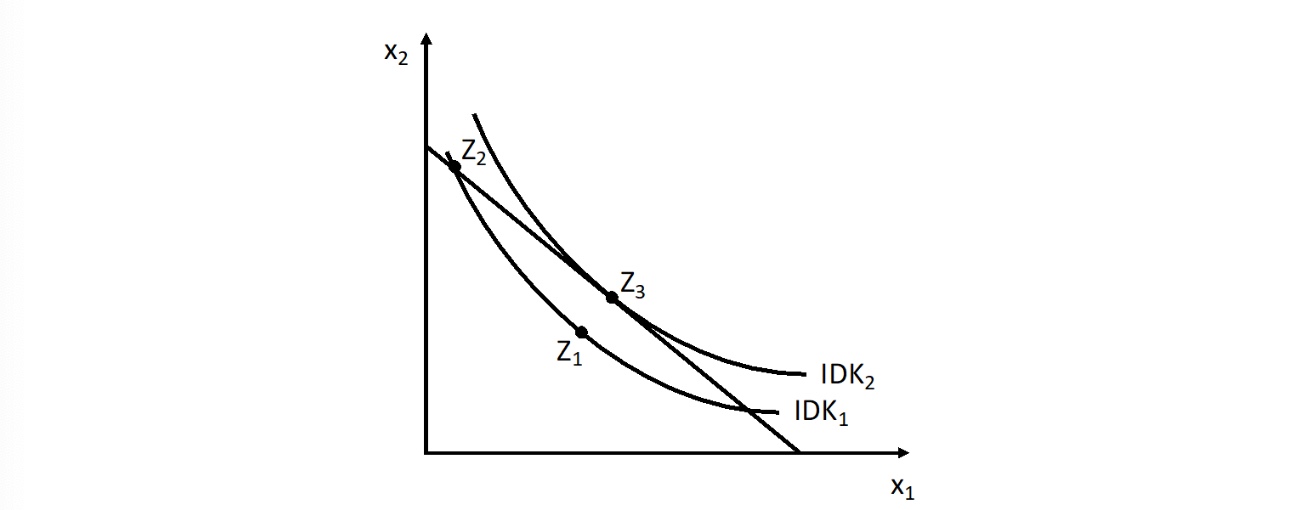
• \(Z_1 \neq\) optimal, da nicht auf B

• \(Z_2 \neq\) optimal, da weniger Nutzen als \(Z_3\)

• \(Z_3 =\) optimal , da maximaler Nutzen und auf Budgetgerade

Wenn \(|MRT| = |MRS| \implies\) optimal $$ \text{Formeln} \ |MRS| = \frac{d x_2}{d x_1} \bigg|_U =

• \frac{\frac{\partial U}{ \partial x_1}}{\frac{\partial U}{ \partial x_2}} \gets \text{subjektive Opport. Kost.}\

|MRT| = \frac{d x_2}{d x_1} \bigg|_B =

• \frac{p_1}{p_2} \gets \text{objektive Opport. Kost.} \

\text{umgeschrieben: } \frac{ \frac{\partial U}{ \partial x_1}}{p_1} = \frac{ \frac{\partial U}{ \partial x_2}}{p_2} $$

Beispiel aus Skript

ein Haushalt mit

• Budgetgerade \(12 = 3 x + 2y\)

• Nutzenfunktion \(U = x^2 y^2\)

Berechnung der MRS $\( \to MU_x = 2x y^2 \\ \to MU_y = x^2 2y \\ MRS = \frac{MU_x}{MU_y} = \frac{2x y^2}{2x^2 y} \xrightarrow{kuerzen} \frac{y}{x} \)\( Berechnung der MRT: \)-\frac{p_1}{p_2} = - \frac{3}{2}$

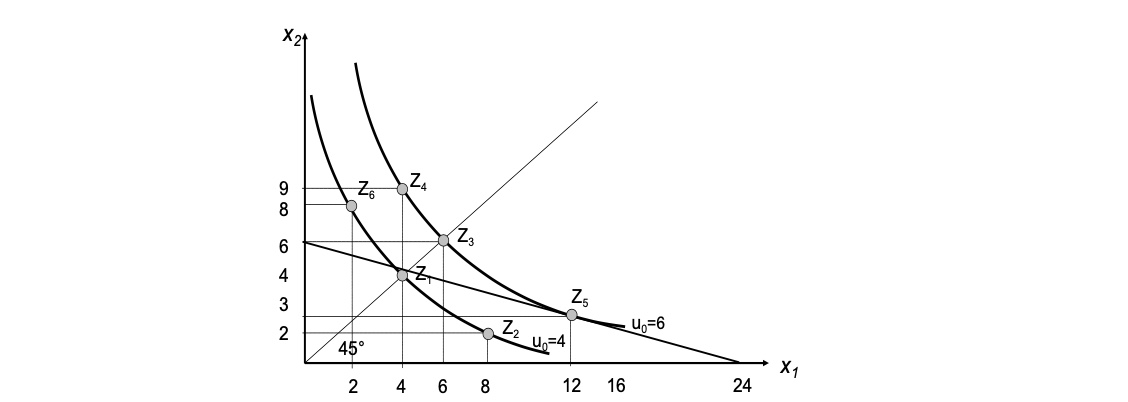
Übung: Haushaltsentscheidungen

Aufgabe 1

Nutzenfunktion: \(U(x_1, x_2) = x_1^{0,5}, x_2^{0,5} \)

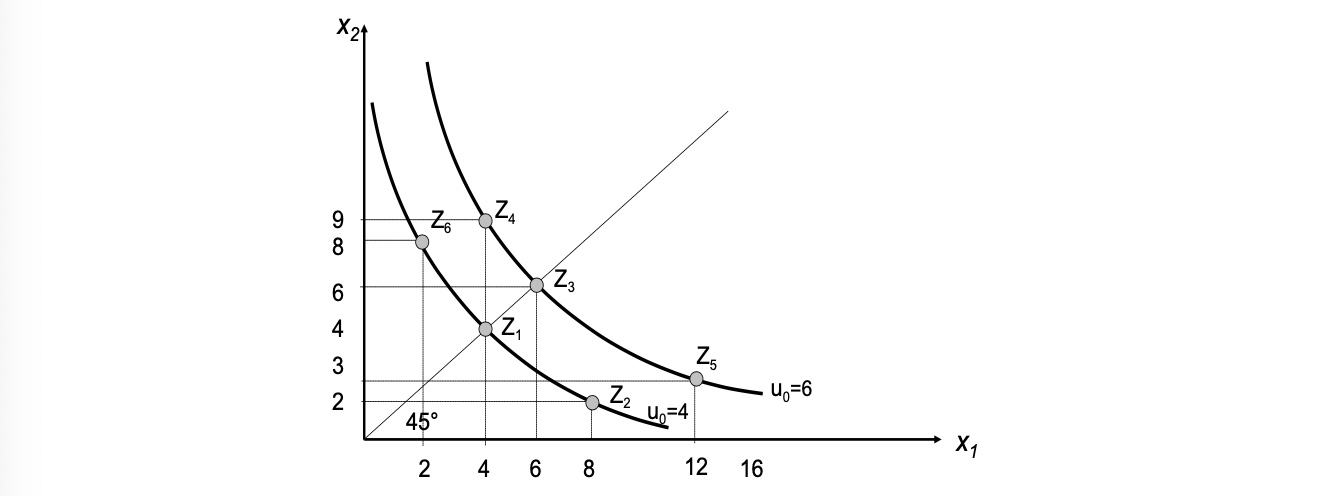
Güterbündel: (und dazugehöriger Nutzen)

• (4,4) -> u = 4

• (8,2) -> u = 4

• (2,8) -> u = 4

• (6,6) -> u = 6

• (4,9) -> u = 6

• (12,3) -> u= 6

=> zwei Indiffierenzkurven $\( \text{allgemeine Form: } U = x_1^{0,5}, x_2^{0,5} \\ \to x_2 = \frac{U^2}{x_1} \\ \text{für u=4: } x_2 = \frac{16}{x_1} \\ \text{für u=6: } x_2 = \frac{36}{x_1} \\ \)$ MRS berechnen:

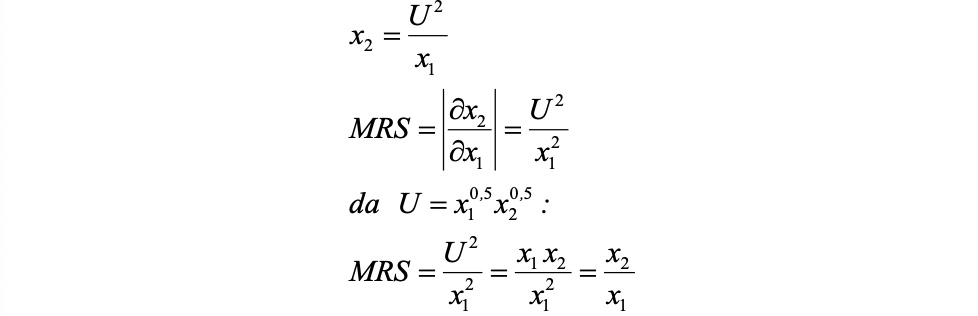
Graphische Darstellung:

Steigung der Kurven durch Ableitung: \(\frac{x_2}{x_1}\)

Lagrange Ansatz (2c)

• Nutzenfunktion: \(U = x_1^{0,5}* x_2^{0,5} \)

• Budgetrestriktion: \(x_1 + 4x_2 = 24\)

Maximierungsproblem: $\( max U = max(x_1^{0,5}* x_2^{0,5}) \\ s.t \\ p_1 x_1+p_2 x_2 = B \)$

1: Lagrangefunktion: (mit jeweiligen 3 Ableitungen)

\[ \begin{align}\begin{aligned}\begin{split} L = x_1^{0,5}* x_2^{0,5} + \lambda * [B- p_1*x_1 - p_2 *x_2] \\ \end{split}\\\begin{split}\to \frac{\partial L}{\partial x_1} = x_1^{-0,5}* x_2^{0,5} - \lambda p_1 = 0 \\ \to \frac{\partial L}{\partial x_2} = x_1^{0,5}* x_2^{-0,5} - \lambda p_2 = 0 \\ \to \frac{\partial L}{\partial \lambda} = B- p_1*x_1 - p_2 *x_2 \end{split}\end{aligned}\end{align} \]

merke: erst aufstellen, dann einsetzen!

2: Umstellen der ersten beiden Ableitungen

\[\begin{split} x_1^{-0,5}* x_2^{0,5} - \lambda p_1 = 0 \to \lambda =\frac{0,5x_2^{0,5} }{p_1 x_1^{0,5}} \\ x_1^{0,5}* x_2^{-0,5} - \lambda p_2 = 0 \to \lambda =\frac{0,5x_1^{0,5} }{p_2 x_2^{0,5}} \end{split}\]

3: Gleichsetzen

\[ x_2 = \frac{p_1}{p_2} x_1 \]

4: Einsetzen in dritte Gleichung

\[\begin{split} B - p_1 x_1 - p_2 \mathbf{\frac{p_1}{p_2} x_1} = 0 \\ B = 2 * p_1 x_1 \end{split}\]

5: optimales Güterbündel

umstellen des Letzen $\( \to x_1^* = \frac{B}{2p_1} \\ \to x_2^* = \frac{B}{2p_2} \)\( und dann Einsetzen der konkreten Werte \)\( x_1^* = \frac{B}{2p_1} \to \frac{24}{2} = 12 \\ x_2^* = \frac{B}{2p_2} \to\frac{24}{8} = 3 \)$ das optimale Bündel ist (12,3)