15.05.2022 Kapitalmarkt#
Was passiert, wenn Haushalte die Möglichkeit haben Geld anzulegen / zu leihen?
=> Erfindung des Bankensystems!
intertemporale Budgetbeschränkung#
gegenwärtige Wert zukünftiger Auszahlungen \(B = \frac{m}{(1+r)^t}\)
m = heutige Einzahlung
r = Zins
Entscheidung eines Haushalts zwischen Gütern in zwei Perioden
\(x_{p2}, x_{p1}\) = Güter in Periode 1/2
\(m_1,m_2\) = Einkommen in Periode 1 / 2
Preise der Güter sind konstant und gleich 1
Güterkonsum in Periode 2, wenn Haushalt in Periode 1 anlegen kann: $\( x_{p2} = m_2 + (m_1 -x_{p1}) + r*(m_1 - x_{p1}) \\ = m_2 + (1+r) * (m_1 - x_{p1}) \)\( alternativ: Haushalt kann in Periode 1 Geld leihen \)\( x_{p2} = m_2 - (x_{p1} - m_1) - r*(x_{p1} - m_1) \\ = m_2 - (1+r)*(x_{p1} - m_1) \\ = m_2 + (1+r)*(m_1-x_{p1}) \)$ = gleiche Mengenfunktion wie davor
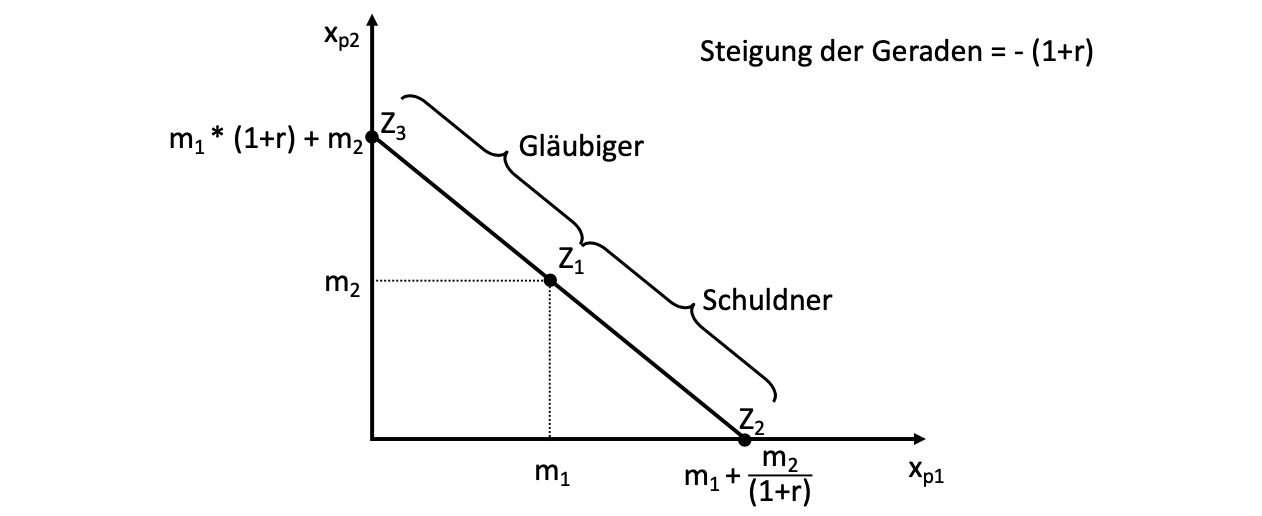
intertemporale Konsumpräferenzen#
wie lässt sich die Präferenz eines Haushalts zwischen zwei Zeitpunkten beschreiben?
Ziel: maximiere den Gesamtnutzen in beiden Perioden
Lagrange Funktion aufstellen: $\( \begin{aligned} L = U(x_{p1}, x_{p2}) &+ \lambda \ [m_1 * (1+r) + m_2 - (1+r)x_{p1} - x_{p2}] \\ &\to \frac{\partial L}{\partial x_{p1}} = \frac{\partial U}{\partial x_{p1}} - \lambda * (1+r) = 0 \\ & \to \frac{\partial L}{\partial x_{p2}} = \frac{\partial U}{\partial x_{p2}} - \lambda = 0 \\ &\to \frac{\partial L}{\partial \lambda} = m_1 * (1+r) + m_2 - (1+r)x_{p1} - x_{p2} = 0 \\ \end{aligned} \)\( Umstellen für die Zeitpräferenzrate \)\( \implies \frac{\frac{\partial L}{\partial x_{p1}}}{\frac{\partial L}{\partial x_{p2}}} = 1+r \text{ oder } \frac{MU(x_{p1})}{MU(x_{p2})} = 1+r \\ r = \frac{MU(x_{p1})}{MU(x_{p2})} - 1 \\ r = \frac{MU(x_{p1})}{MU(x_{p2})}- \frac{MU(x_{p2})}{MU(x_{p2})} \\ r = \bold{\tau = \frac{MU(x_{p1})- MU(x_{p2})}{MU(x_{p2})}} \)$ Analogie Betrachtungen dieser Formeln
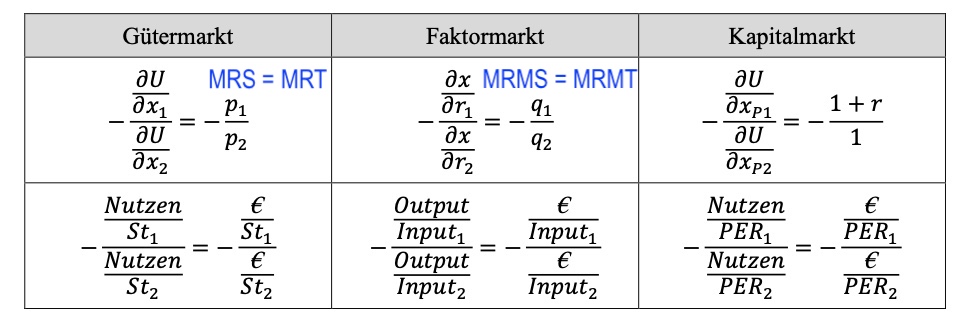
Betrachtung der temporalen Konsumpräferenzen
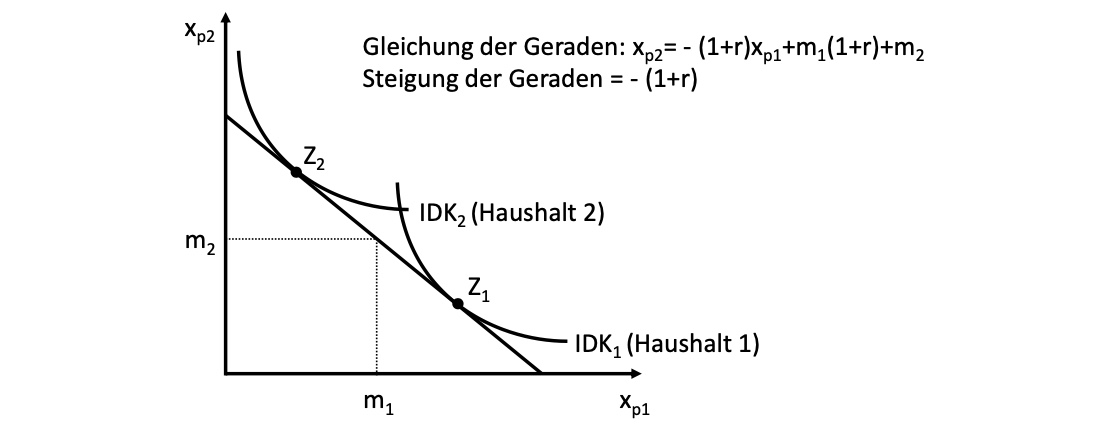
Haushalt 1: hohe Gegenwartspräferenz in Punkt \(Z_1\), Verschuldung in Periode 1
Haushalt 2: hohe Zukunftspräferenz, Kapitalanlage in Periode 1
Berechnung der Zinsrate: Realzins = Nominalzins - Inflationsrate
Übung#
Aufgabe 1: intertemporaler Konsum#
Konsument woll über zwei Jahre optimieren, ohne Möglichkeit anzulegen / Schulden zu machen!
Nutzenfunktion: \(U(x_1,x_2) = x_1^{0.5} x_2^{0.5}\)
für Funktionsgleichung nach \(x_2\) umstellen (Ordinaatenachse)
für U=100 : \(x_2 = 10000/x_1\)

2 Aufgabe: Intertemporale Budgetgerade#
Haushalt mit Einkommen = 100 GE pro Jahr und r=5%
Bestimmung der Gleichung der Budgetgerade:
Steigung der Gerade = MRT = 1+r
\(r=0.5 \to MRT = 1.05\)
Schnittpunkt der Gerade mit Ordinate = SPO = B+B(1+r) = B(2+r)
\(B=100 \to SPO = 205\)
Somit: \(x_2 = -MRT * x_1+SPO = -(1+r)x_1+B(2+r)\)
\(x_2 = -1.05x_1 + 205\)
\(SPA = \frac{205}{1.05} = 195.23 \)
graphisch: 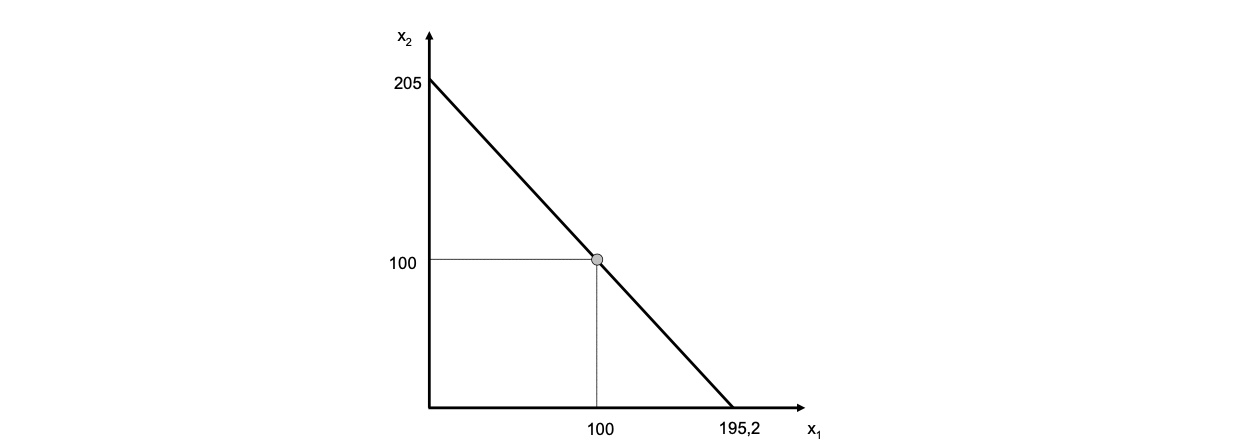
Aufgabe 3: Intertemporales Gleichgewicht#
Maximierungsproblem mit Lagrange $\( \underset{x_1,x_2}{maxU} = \underset{x_1,x_2}{max}(x_1^{0.5} x_2^{0.5}) \\ s.t. \\ x_2 = -(1+r)*x_1+B(2+r) \)\( Lagrange Funktion und Ableitung: \)\( \begin{aligned} LF &=x_1^{0.5} x_2^{0.5} + \lambda[x_2 + (1+r)*x_1 - B(2+r)] \\ \\ \frac{\partial L}{\partial x_1} &= 0.5x_1^{-0.5} * x_2^{0.5} + \lambda(1+r) = 0 \\ \frac{\partial L}{\partial x_2} &= 0.5x_2^{-0.5} * x_1^{0.5} + \lambda= 0 \\ \frac{\partial L}{\partial \lambda} &= x_2 + (1+r)*x_1 - B(2+r) = 0 \end{aligned} \)\( Auflösen der ersten Ableitungen nach Lambda und Gleichsetzen \)\( \lambda = \frac{0.5x_1^{-0.5} * x_2^{0.5}} {(1+r)} \\ \lambda = 0.5x_2^{-0.5} * x_1^{0.5} \\ 0.5x_2^{-0.5} * x_1^{0.5} = \frac{0.5x_1^{-0.5} * x_2^{0.5}} {(1+r)} \ \bigg|*2; :x_2^{-0.5} \\ x_1^{0.5} = \frac{x_1^{-0.5} * x_2^{0.5}} {(1+r) *x_2^{-0.5}} = \frac{x_1^{-0.5}} {(1+r)} * x_2 \ \bigg|:x_1^{-0.5} \\ x_1 = \frac{1}{(1+r)}*x_2 = \frac{x_2}{(1+r)} \)\( Einsetzen in die Lambda-Ableitung 3 \)\( x_2 + (1+r)* \frac{x_2}{(1+r)} - B(2+r) = 0 \\ 2x_2 - B(2+r) = 0 \\ x_2^* = \frac{B(2+r)}{2} \)\( Rücksubstitution in \)x_1\( Optimum: \)x_1^* = \frac{B(2+r)}{2(1+r)}$
Das ist allgemein anwendbar für die spezifische Nutzenformel
für B=100 und r=0.5 $\( x_1 = \frac{100*(2.05)}{2*1.05} = 97.61 \\ x_2 = \frac{100*2.05}{2} = 102.5 \\ U = x_1^{0.5} x_2^{0.5} = 97.61^{0.5}* 102.5^{0.5} = 100.025 \)$
Der Haushalt würde im ersten Jahr ~2.39 GE sparen und im zweiten Jahr das konsumieren
Daraus zieht er einen um 0.025 höheren Nutzen als ohne Kapitalmarkt
Graphisch: 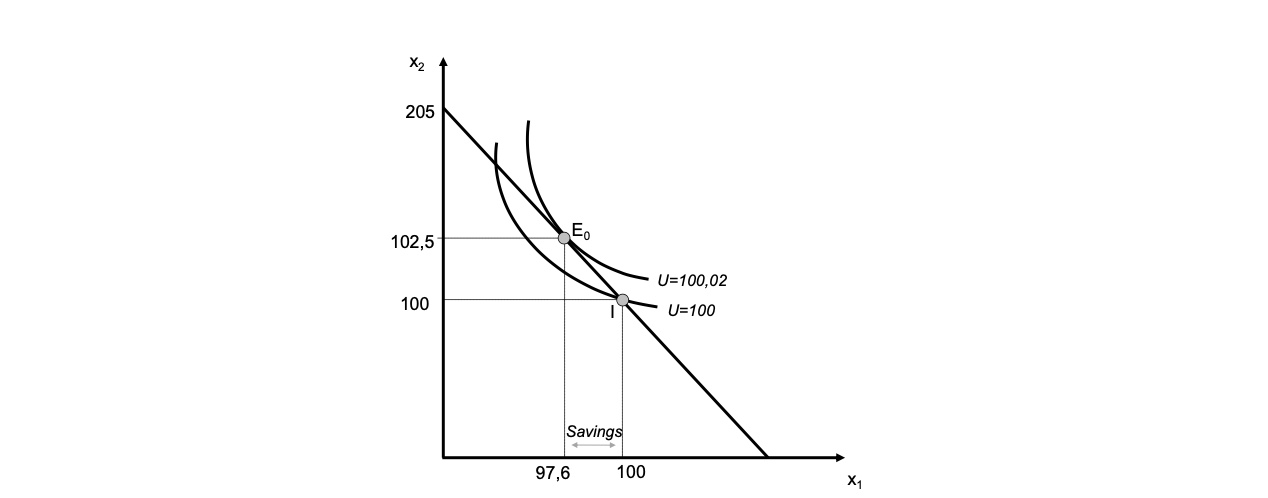
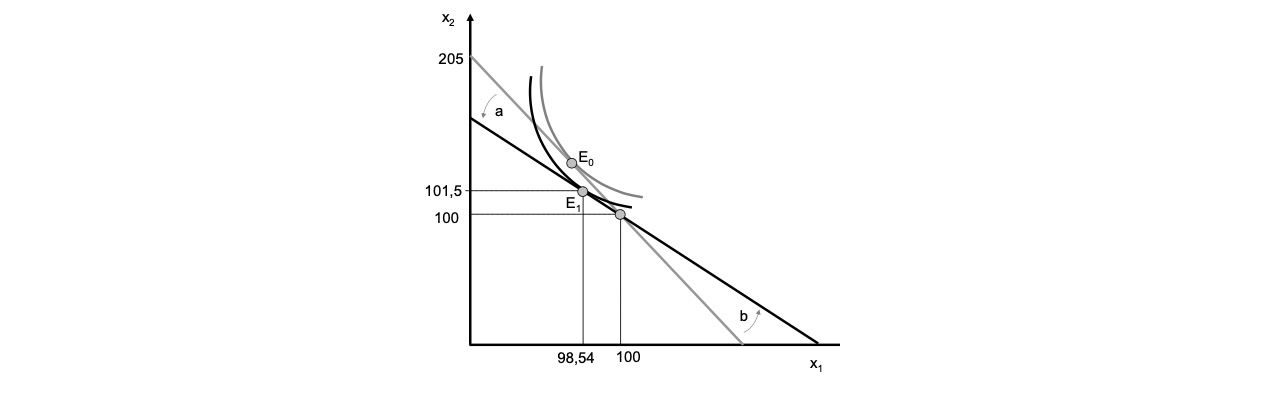
Aufgabe 4: Schocks#
Zinsatz sinkt auf 3%, Budget bleibt
Budgetgerade: \(-(1+r)x_1+B(2+r) = -1.03x_1+203\)
SPO = 203, SPA = 197,1
neue Optima:
\(x_2^* = \frac{B(2+r)}{2} = 101.5\)
\(x_1^* = \frac{B(2+r)}{2(1+r)} = 98.54\)
\(U = 101.5^{0.5} * 98.54^{0.5} = 100.01 \)
Der Haushalt zeiht Nutzen aus dem Kapitalmarkt, aber weniger als davor
Graphisch: Zinsratenänderung = Drehung der Budgetgerade