27.05.2022 Gaussche Normalverteilung#
„Fehlerverteilung“, oft in Naturwissenschaften

Dichtefunktion: \(f(x)= \frac{1}{\sqrt{2\pi} * \sigma} * exp \Big( - \frac{(x-\mu^2)}{2 \sigma^2}\Big)\)
Erwartungswert = \(\mu\)
Varianz = \(\sigma^2\)
graphische Darstellung:
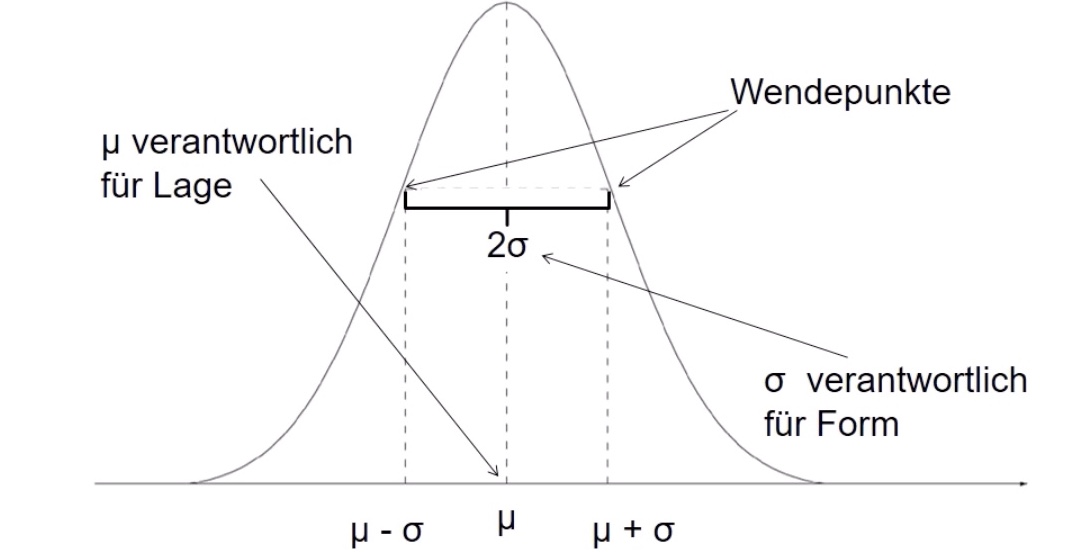
beachte:
Kurve konvergiert gegen 0, erreicht aber nicht
Fläche unter Kurve = 1
Standardnormalverteilung#
Falls \(\mu = 0\) und \(\sigma^2 = 1 \to\) N(0,1) = Standardnormalverteilung
Dichtefunktion: \(f(x)= \frac{1}{\sqrt{2\pi}} * exp \big( - \frac{x^2}{2}\big)\)
Bezeichnung: \(\Phi(x)\)
Standardisierung#
Verteilung X auf Standardnormalverteilung N(0,1) formieren $\( X \sim N(\mu, \sigma^2) \implies Z \sim N(0,1) \\ Z =\frac{X-E(X)}{\sqrt{Var(X)}} = \frac{X-\mu}{\sigma} \)$
Symmetrie#
Dichte der Normalverteilung ist „symmetrisch“
Also: \(\Phi(-z) = 1- \Phi(z)\)
Berechnung von Wahrscheinlichkeiten#
\(P(a \le X \le b)\) Gegeben \(X \sim N(\mu, \sigma^2)\) ?
bei Standardnormalverteilung:#
\(\implies P(a \le X \le b) = F(b) - F(a) = \Phi(b)- \Phi(a)\)
Nun bestimmung mithilfe von Rechnern / Tabellen
vorgegeben in Klausuren / Skript: 
nicht Standardnormalverteilung#
wenn nicht Standardnormalverteilung => transformieren (auch die Grenzen a, b) $\( P(a \le X \le b) = P\Big(\frac{a-\mu}{\sigma} \le \frac{X-\mu}{\sigma} \le \frac{b-\mu}{\sigma} \Big) \\ = P\Big(\frac{a-\mu}{\sigma} \le Z \le \frac{b-\mu}{\sigma} \Big) = \underbrace{ \Phi \Big(\frac{b-\mu}{\sigma} \Big)- \Phi \Big(\frac{a-\mu}{\sigma} \Big)}_{\text{Grenzen transformieren!}} \)\( oder \)P(X \le x) = \Phi \big(\frac{x- \mu}{\sigma} \big)$
Beispiele#
Standardnormalverteilung: $\( P(Z \le -0.8) = \Phi(-0.8) = 1 - \underbrace{ \Phi(0.8)}_{\text{Tabelle}} = 1- 0.7881 = \bold{0.2119} \\ \)\( Normalverteilung: \)\( \begin{aligned} X \sim N(4,49) &\implies \mu = 4; \sigma = \sqrt{49} = 7 \\ \\ P(X \le 5) &= \Phi \Big(\frac{x-\mu}{\sigma} \Big) = \Phi \Big(\frac{5-4}{7} \Big) \\ &= \Phi(1/7) \\ \\ P(3 \le X \le 5) &= \Phi \Big(\frac{5-4}{7} \Big) - \Phi \Big(\frac{3-4}{7} \Big) \\ &= \Phi \Big(\frac{1}{7} \Big) - \Phi \Big(-\frac{1}{7} \Big) \\ &= \Phi \Big(\frac{1}{7} \Big) - \Big[1- \Phi \Big(\frac{1}{7} \Big)\Big] \\ &= 2 * \Phi \Big( \frac{1}{7} \Big) -1 = 0.1138 \end{aligned} \)$
In R:
p = 5 # der gesuchte Wert
m = 4 # das mu der Verteilung
sd = 7 # die Standardabweichung
# Berechnung der Wahrscheinlichkeit mit pnorm()
pnorm(p,m,sd)
Output:
0.5567985
wenn nicht unterhalb der Wert gesucht wird, sondern oberhalb:
pnorm(p,m,sd,lower.tail=FALSE)
anderes Beispiel:
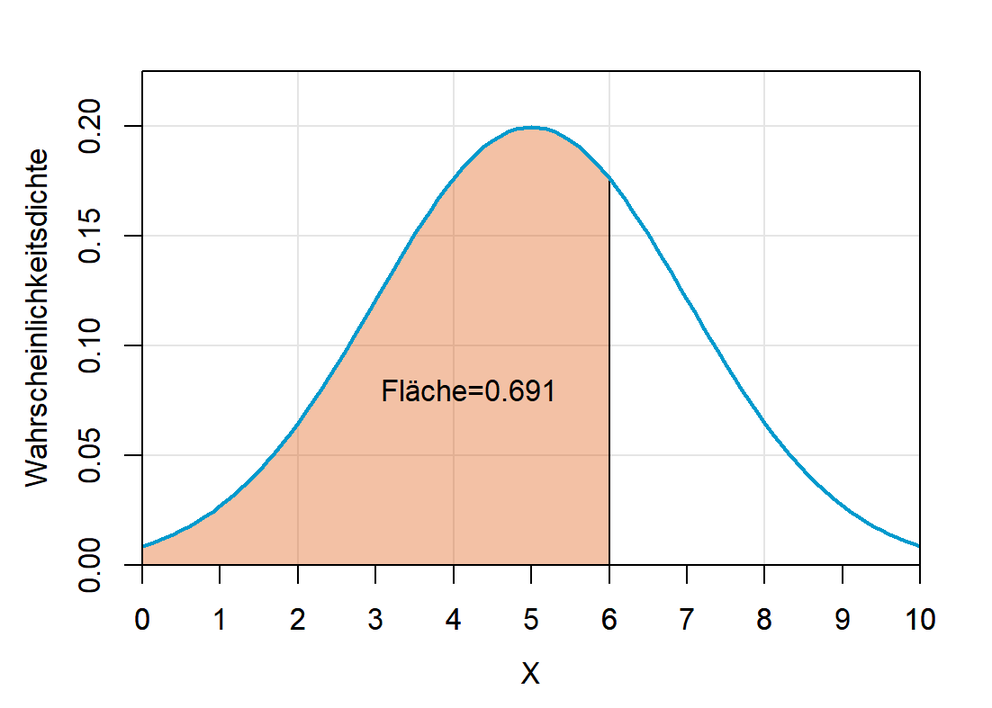
p = 6 # der gesuchte Wert
m = 5 # das mu der Verteilung
sd = 2 # die Standardabweichung
# Berechnung der Wahrscheinlichkeit mit pnorm()
pnorm(p,m,sd)
# 0.691
Darstellung: