07.06.2022 Tests#
Testproblem#
Nullhypothese \(H_0\): „die Erde ist eine Scheibe“
Alternativhypothese \(H_1\): „Erde hat Kugelgestalt“
=> Testproblem: \(H_0\) vs. \(H_1\)
Beispiel#
Schmecken Leitungswasser und Mineralwasser gleich?
\(H_0\): schmecken Gleich
\(H_1\): schmecmen unterschiedlich
Lasse Personen testen und messe Anteil Personen, die Leitungswasser besser finden
= Bernoulli Model mit Erfolgswahrscheinlichkeit p
\(H_0: p = 0.5\) (kein Unterschied)
50% der Personen entscheiden sich für eins von beidem
\(H_1: p \ne 0.5\) (Unterschied)
unterschiedliche Mengen an Menschen entscheiden sich für eines
Interpretation der Testergebnisse: 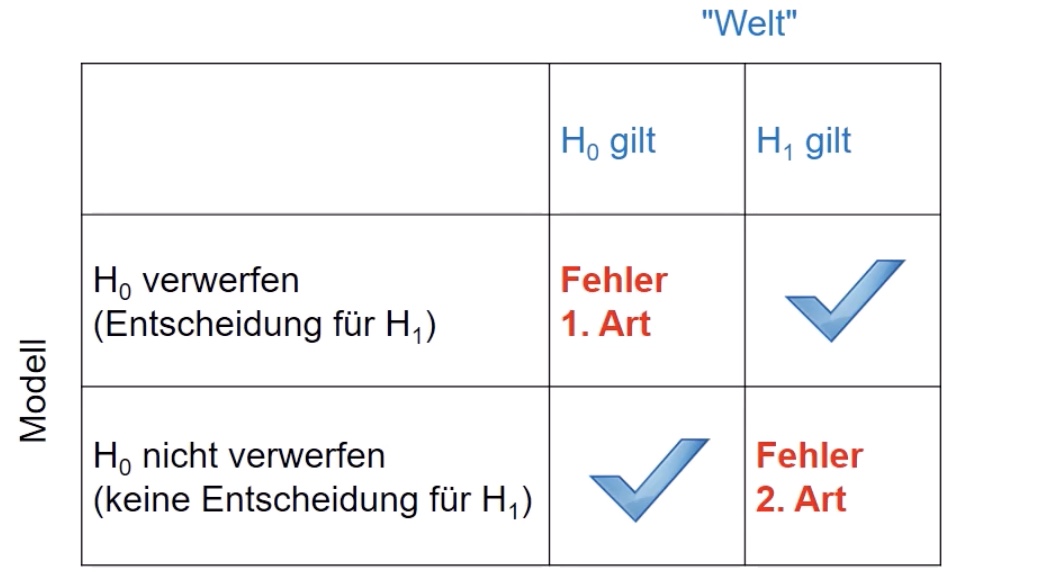
Lösung: konstruiere Entscheidungsregel, sodass Fehler nur mit geringer Wahrscheinlichkeit passieren
Entscheidungsregel: führt zu Entscheidung über Ablehnung oder Beibehalten von \(H_0\)
Problem: bei festem Stichpobenumfang beide Fehler nicht gleichtzeitig minimierbar
Dann:
Fehler 1. Art soll nur mit vorgegebener Wahrscheinlichkeit passieren
erst dann Fehler 2. Art minimieren
Sodass \(P(\text{Fehler 1. Art}) \le \alpha\)
Entscheidungsregel im Wassertest: \(H_0\), wenn \(0.4 > p >0.6\), sonst \(H_1\)