Statistik 1 Zusammenfassung#
Allgemein#
Merkmale#
Merkmal: Untersuchungskategorie mit spezifischer Ausprägung
Notation:
Merkmal \(X,Y,Z\)
Ausprägung \(x_1,x_2,...x_n\)
sortiert: \(x_{(1)},x_{(2)}, ..., x_{(n)}\)
Arten:
nominal: Namenskategorie
ordinal: Rangkategorie / Ordnung
kardinal/metrisch: numerische Ausprägung
Klassen#
Klasse: Zusammenfassung von Ausprägungen in Gruppen
Notation:
k = Anzahl Klassen
\(m_j\) = Klassenmitte
\(n_j\) = Anzahl Beobachtungen in Klasse
Wahl der Klassen (nur Daumenregeln)
gleichmäßige Verteilung
gleiche Klassenbreite
Anzahl Klassen = \(\sqrt{n}\) (Wurzel der Anzahl Ausprägungen gesamt)
offene Randklassen möglich (beispielsweise ins Unendliche)
Wertebereiche
[0-100] = einschließlich 0 und 100
(0-100) = auschließlich 0 und 100
[0-100) = einschließlich 0, auschließlich 100
Darstellungen#
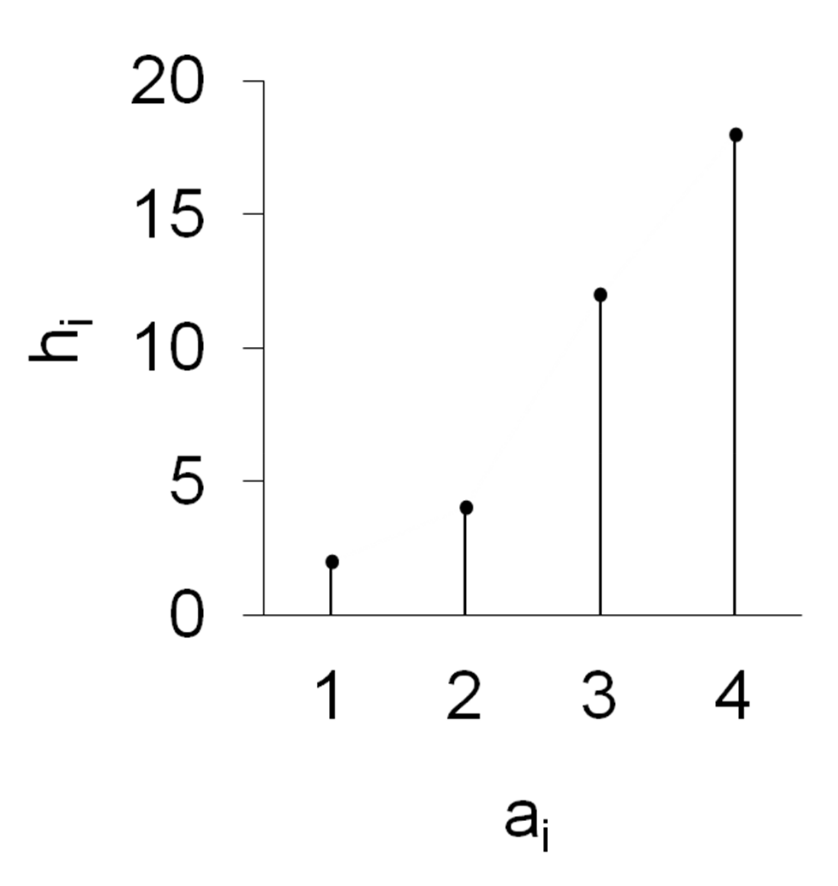
Stabdiagramm |
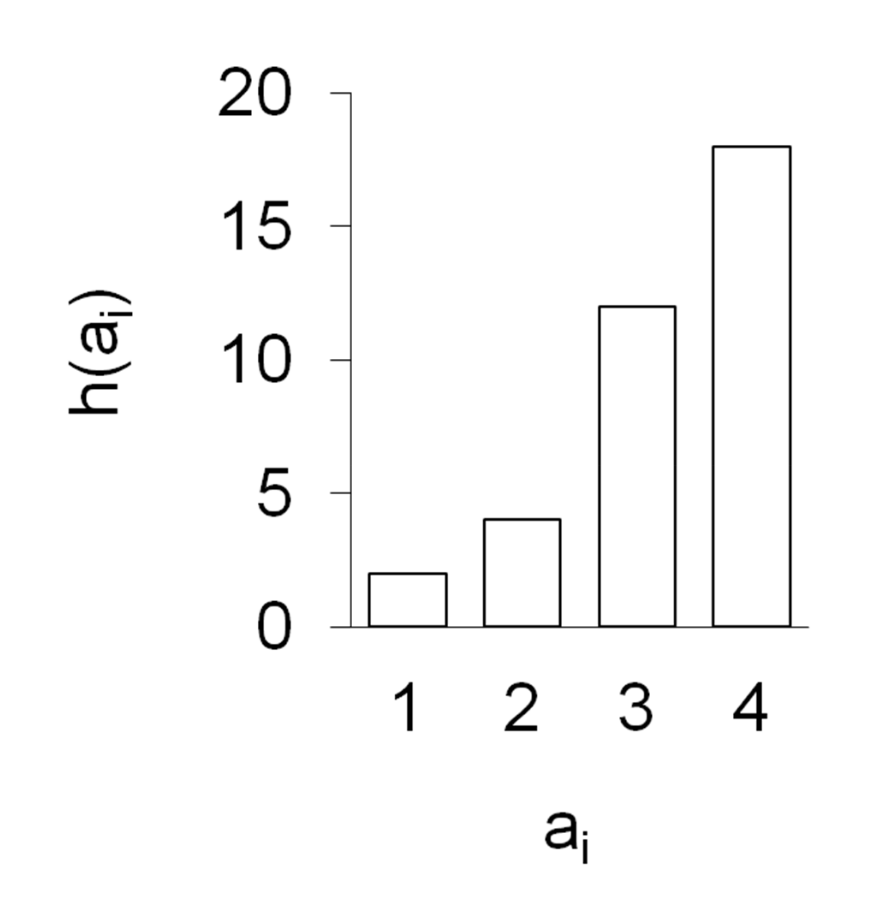
Säulendiagramm |
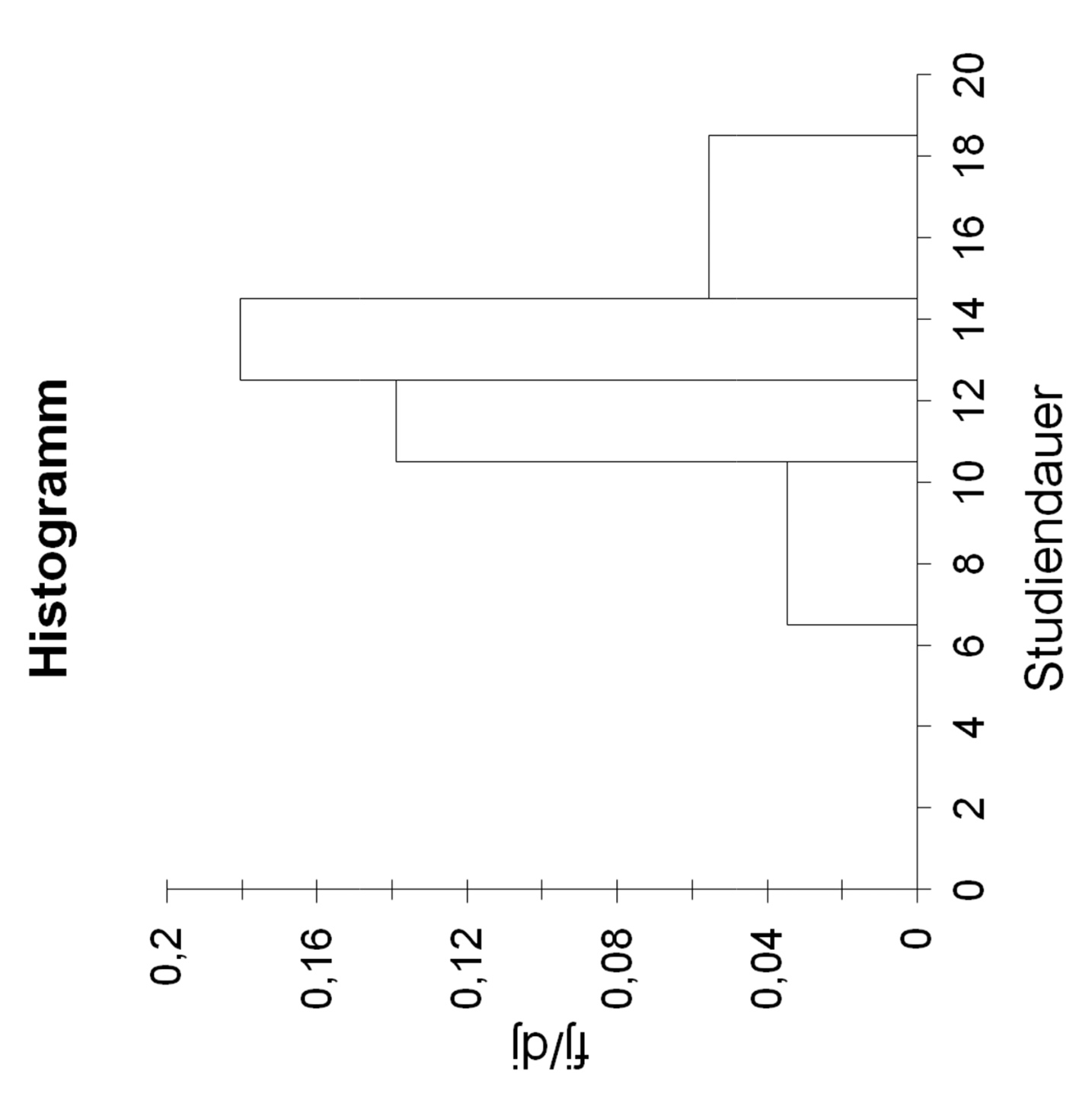
Histogramm |
|---|---|---|
|
|
|
längentreu: Länge der Stäbe = Information |
längentreu: Länge der Balken; alle gleiche Breite + gleicher Abstand |
flächentreu: Fläche der Balken = Information; Breite = Klassenbreite |
Kumulierte Häufigkeitsverteilung#
Empirische Verteilungsfunktion: Berechnung der Anteile ober/unterhalb von bestimmter Grenze: \(F(x)= \sum_j^i n(x_j)\)
für Merkmal X mit \(x_1,...,x_n\)
für jedes x Anteil der Werte < x
Beispiel:
\(a_j\) |
\(h_j\) |
\(f_j\) |
\(kum \ f_j\) |
|---|---|---|---|
cool |
10 |
10/30 = 0.333 |
0.333 |
uncool |
20 |
20/30 = 0.666 |
0.333+0.666 = 1 |
\(\sum = 30\) |
1 |
Lagemaße#
Indikatoren zur Beschreibung der Lage eines Datensatzes
Arithm. Mittel#
benötigt metrisches Skalenniveau
Urliste: \(\frac{1}{n} \sum x_i\)
Unklassierte Verteilung: \(\frac{1}{n} \sum a_j * h_j\)
klassierte Verteilung: \(\frac{1}{n} \sum m_j * n_j\)
Geometrisches Mittel#
zur Berechnung von Wachstum
benötigt metrische Merkmale > 0
Wachstumsrate \(r_t = \frac{x_1-x_0}{x_0}\)
Wachstumsfaktor \(w_t = 1+ Rate\)
Durchschnittlicher Wachstumsfaktor \(\bar{w}_{geom} = (\frac{x_n}{x_0})^\frac{1}{n}\)
n = Anzahl Zeitperioden