21.06.2023 Inflation and monetary policy#

Chapter 15

Inflation and Philipps Curve#

Inflation: Increase in general price level, measured by CPI

Real interest Rate \(r = i - \pi^e_{t+1}\) (Fisher Equation)

  • also measured with differnce between inflation indexed bonds and market bonds

rational expectations formulation:

  • no systematic forecast errors

  • use all relevant info (esp. expert forecasts)

  • problem: incomplete models and experts

Problems

  • volatile / high = detrimental

  • investment unsafe

  • income declines

Benefits

  • effective monetary policy (no deflation)

  • redistribution (creditor to debtor)

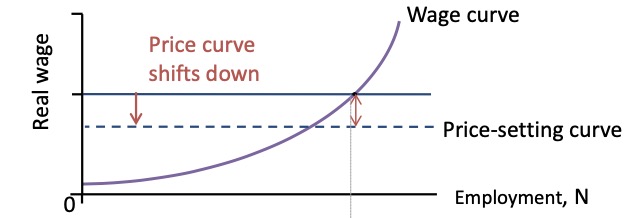
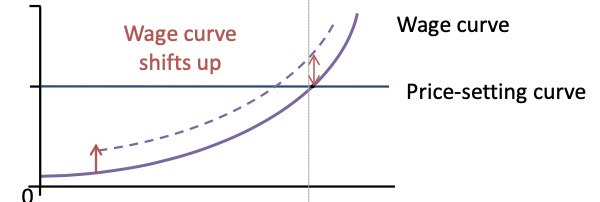
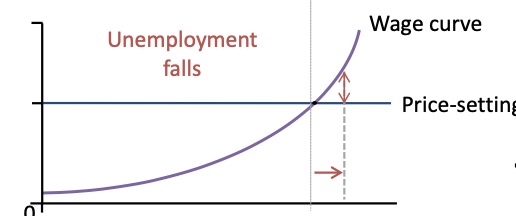
Wage as Inflation Driver#

also: Demand Pull Inflation

  • Owners Power rises (e.g lower comp.)

  • employees power rises (e.g. more people join union)

  • Unempl. falls

Situation

Graphic

Owners Power rises (e.g lower comp.)

img

employees power rises (e.g. more people join union)

img

less unemployment (more power)

img

Philipps Curve: Unemployment and Inflation

img

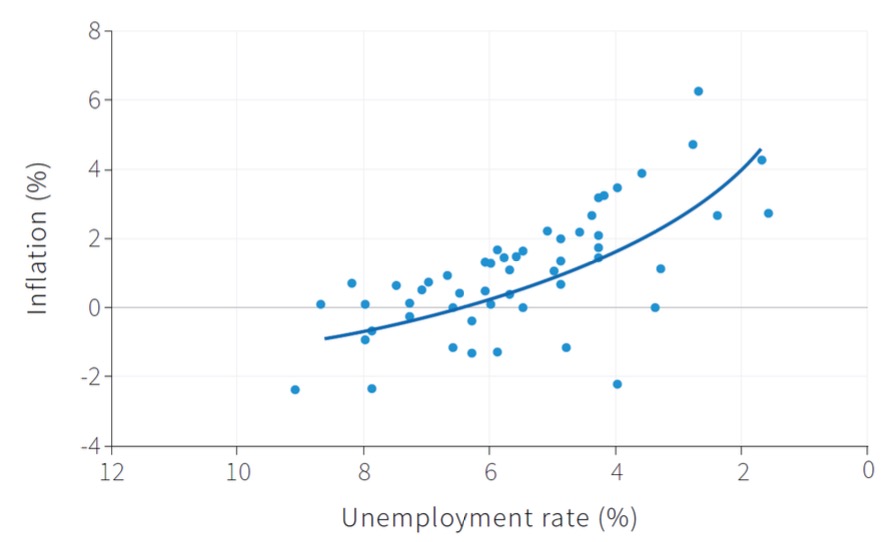
=> curve can shift over time (stagflation)

other reasons: Capacity Constraints (in the short run)

AD, Unemployment and Inflation#

Labor Equilibrium shocks#

Bargaining Gap: Difference between real wage with highest incentive and real wage with highest profit

img

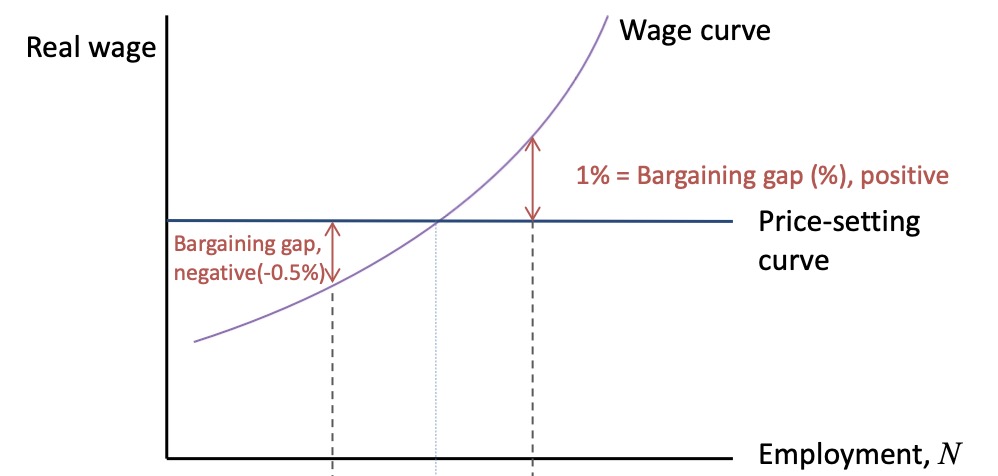
Calculated:

\[ inflation = \frac{ w_{ \text{wage curve}} - w_{\text{price curve}} }{w_{\text{price curve}}} \]

translates to

img

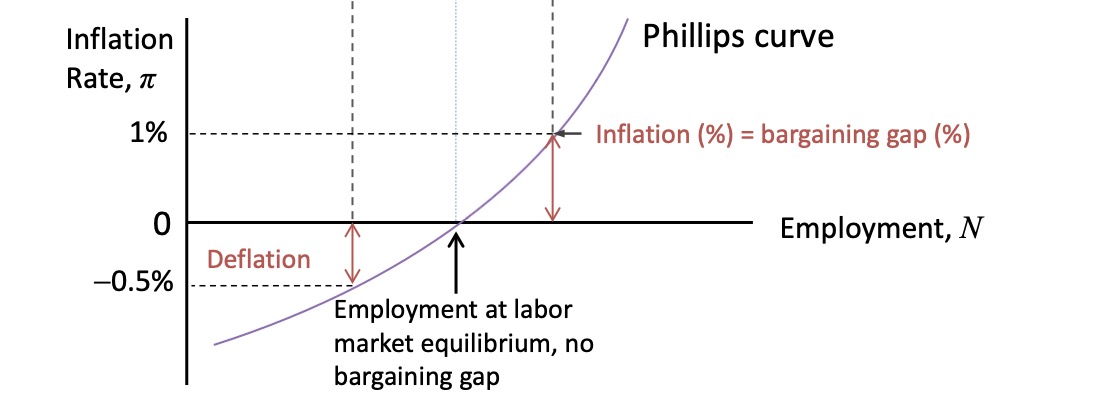
Medium-Run:

  • Boom (higher AD)

    • less unempl.

    • positive bargaining gap

    • positive wage-price spiral

    • Inflation

  • Recession (lower AD): vice versa

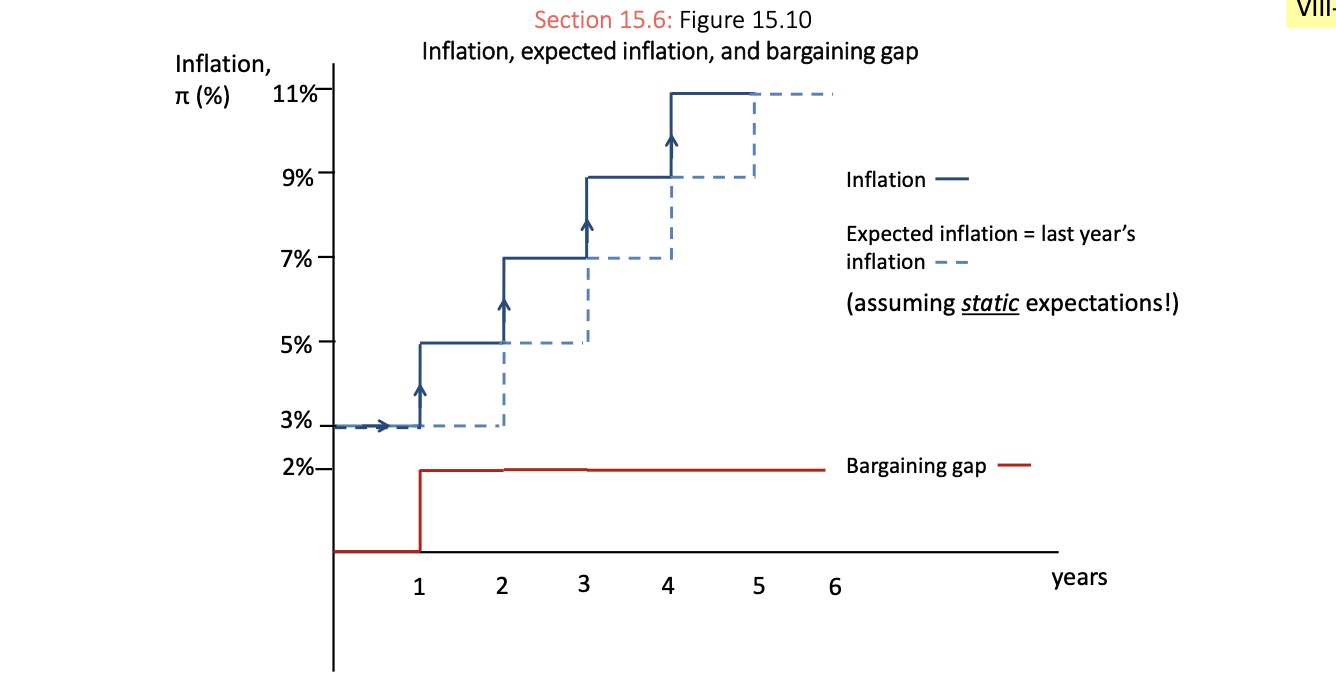
in Boom:

  • workers want real wage rise and inflation combat rise

  • these rises oush next years inflation etc…

img

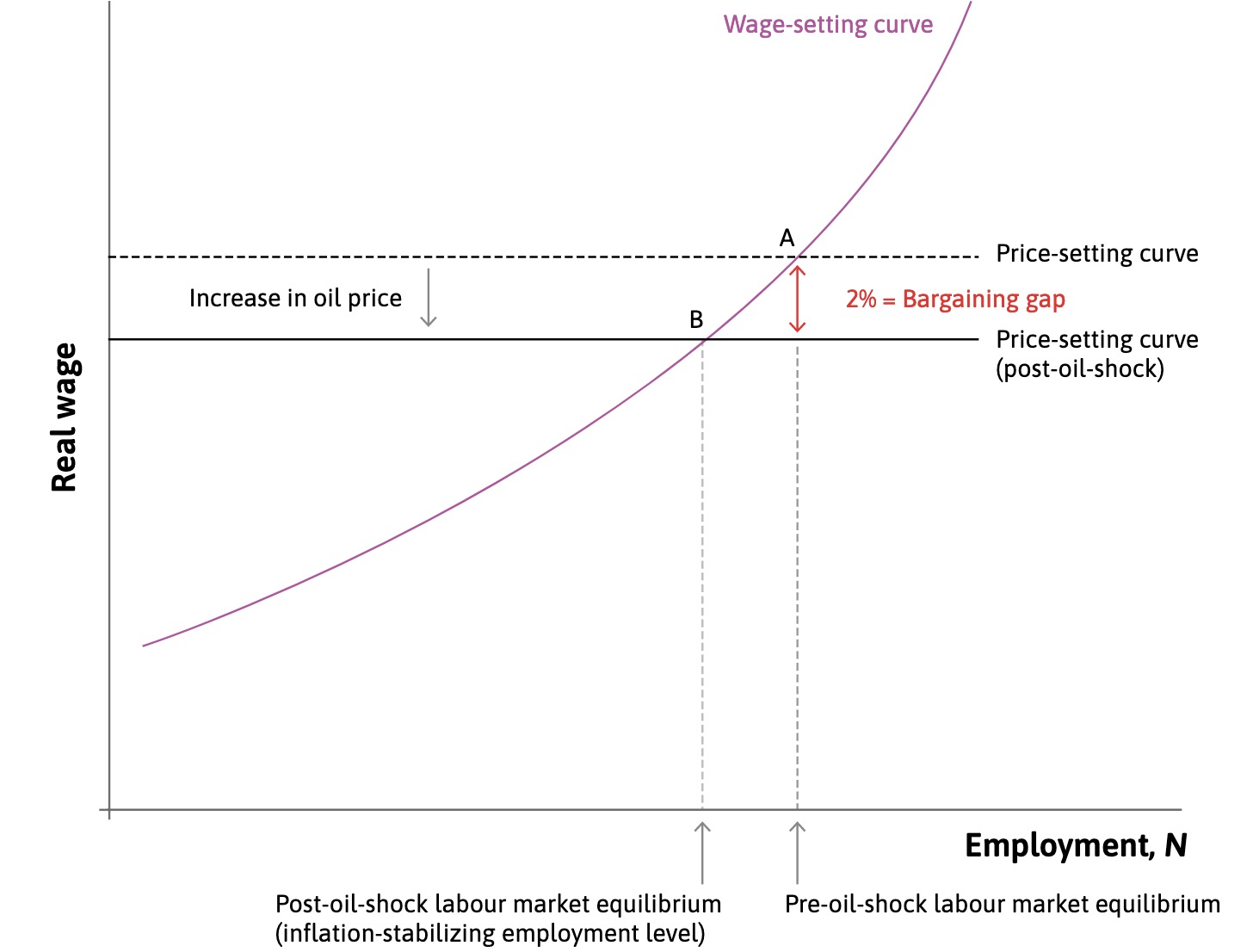
Supply Shocks#

Price Shocks to the material supply:

  • Firms rise prices to protect profits

  • workers lose real purchasing power

=> bargaining gap

img

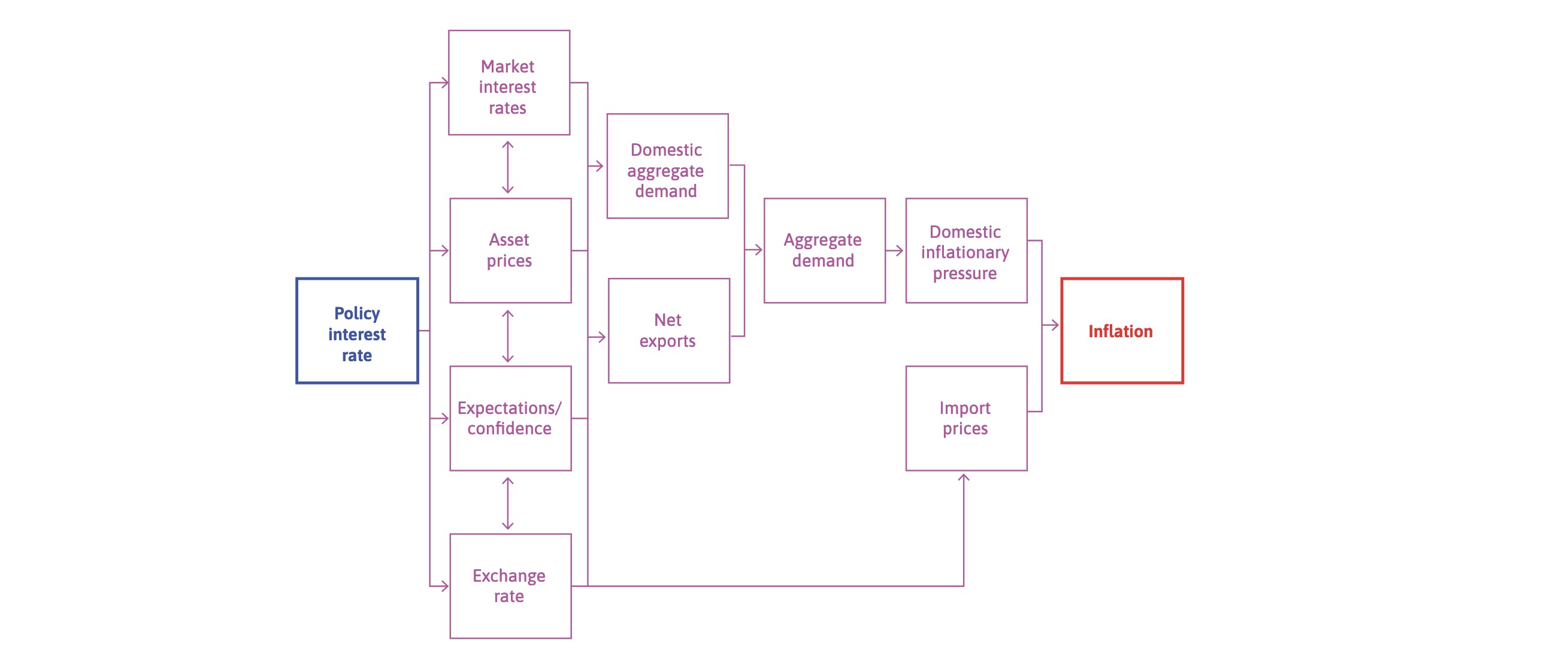
Monetary Policy#

Transmission channels on Inflation

  • market interest rates

  • value of assets

  • expectations

  • exchange rate

img

Limitations:

  • zero lower bound

  • long maturities

=> alternative Quantitative Easing

Interest rate Yield curve#

different interest rates depending on maturity

img

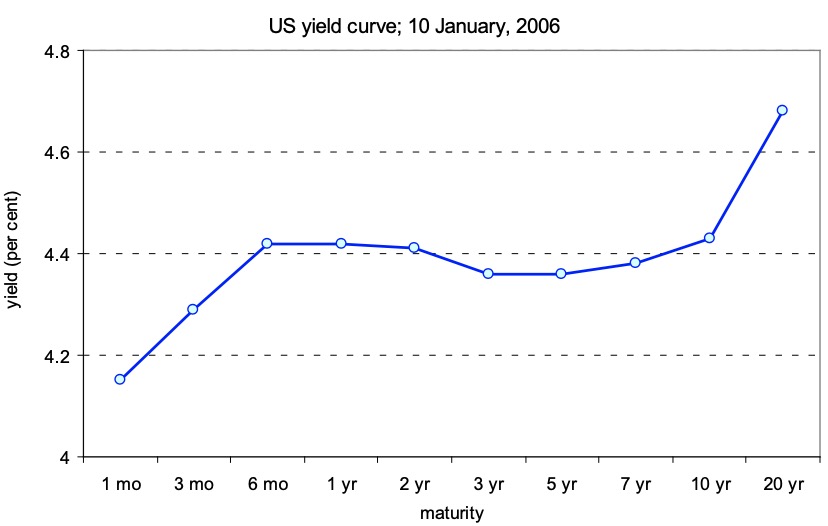
Reason: rational expectations because of higher risks for investors

\[ i_t = \frac{ i_t+ i_{t+1}^e +...+ i^e_{t+n-1} }{n} \]

=> investors arbitrage the interest differences based on the expectations for future interest rates

Barro-Gordon Model#

Model about Central Bank actions with inflation targeting

Loss Function of CB:

\[ L = b(U-U^*)^2 + (\pi - \pi^*)^2 \]

  • \(U / U^*\) = unemployment / target rate for unempl.

  • \(\pi / pi^*\) = inflation / target rate of inflation

  • b = vaulation of other goals beside inflation, here Unemployment

  • higher b = more flexible inflation target

img

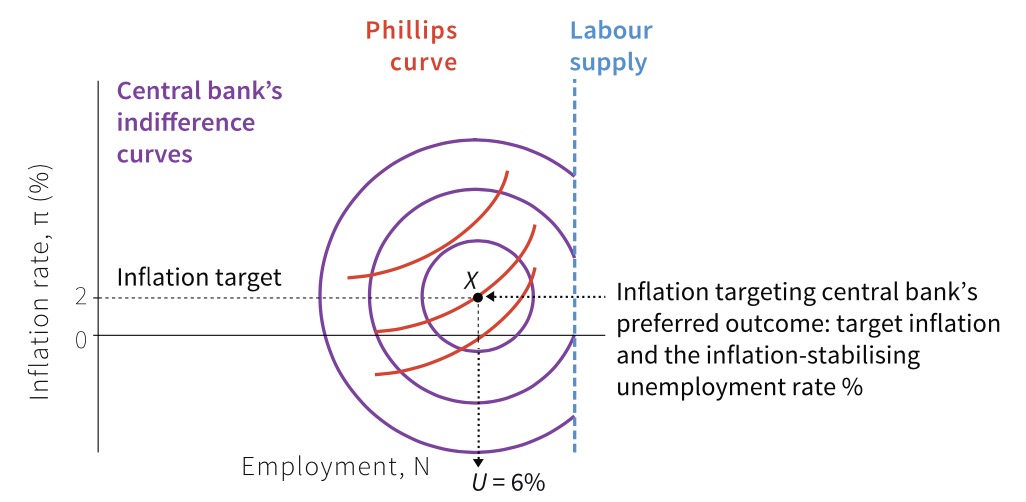
Barro Gordon Model#

Expectations-augmented Philipps Curve:

\[ U = U_n - a (\pi - \pi^e) \]

  • \(U_n\) = natural rate of unemployment

  • when inflation differs from it, then another U possible

Optimal Point (bliss point):

  • \(U^* = k * U_n; 0 < k < 1\)

  • \(\pi^* = 0\)

Combination of L and U Formula and Bliss point

Explanation of this calcukation an graph: what if the central bank is not independent and has the will to lower unemployment? then they will create a surprise inflation:

  • Starting in Point A: expecations = 0, full power to CB

  • Goal is Point B with lower unemployment

  • but Result is D, due to actors incorporating the expected inflation

\[\begin{split} L = b(U-U^*)^2 + (\pi - \pi^*)^2 \\ U = U_n - a (\pi - \pi^e) \\ U^* = k*U_n; \pi^* = 0\\ \implies L = b [ \underbrace{U_n-a (\pi - \pi^e)}_U- \underbrace{k*U_n}_{U^*}]^2 + \pi^2 \\ \frac{ \delta L }{\delta \pi} = 0 \to \frac{ ab [U_n(1-k)+ a\pi^e] }{1+a^2b} \end{split}\]

img

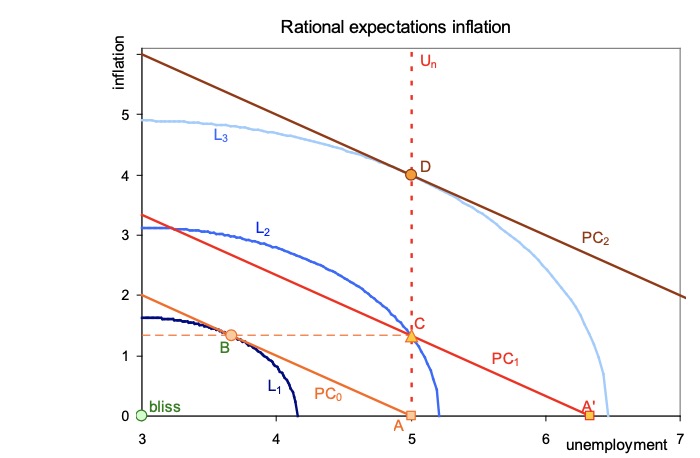
=> Credibility needed

  • Central bank works with expectations

  • higher credibility = easier policy

  • no expected surprise inflation

  • with policy rule = 2% = rational expectation

    • CB stays at Point A

Taylor Rule#

Rule of John Taylor for central banks short term rate $\( i_t-\pi_t = r+a(\pi_t-\pi^*)+\beta x_t \\ with \ x=\frac{ Y -\bar{Y}}{\bar{Y}} = output \ gap \)$ CB should adjust short term rate based on heating of the economy

  • in Euroarea: not possible, due to unified monetary policy

  • and output gap estimation difficult

From the typical euro critics at Axel-Springer:

img

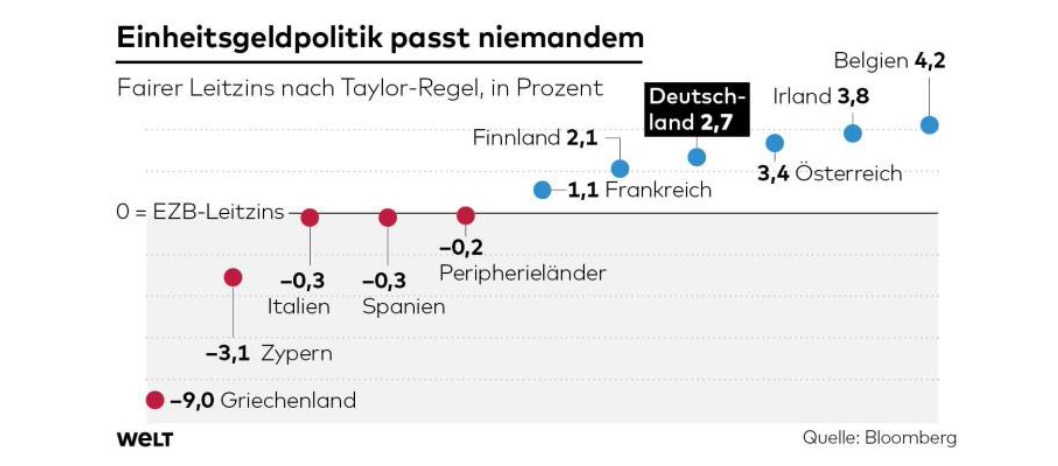
better version of this: Orphanides Rule