18.10.2023 Tools of Public Economics#

Theoretical Framework#

Neoclassical / Mainstream Economics

  • good in predicting individual behavior

  • theory was updated with foundations from other schools of thought

Demand#

for Goods

Constraint Utility Maximization#

Assumption:

  • limited resources

  • individual has utility function

  • Aim = maximize welfare

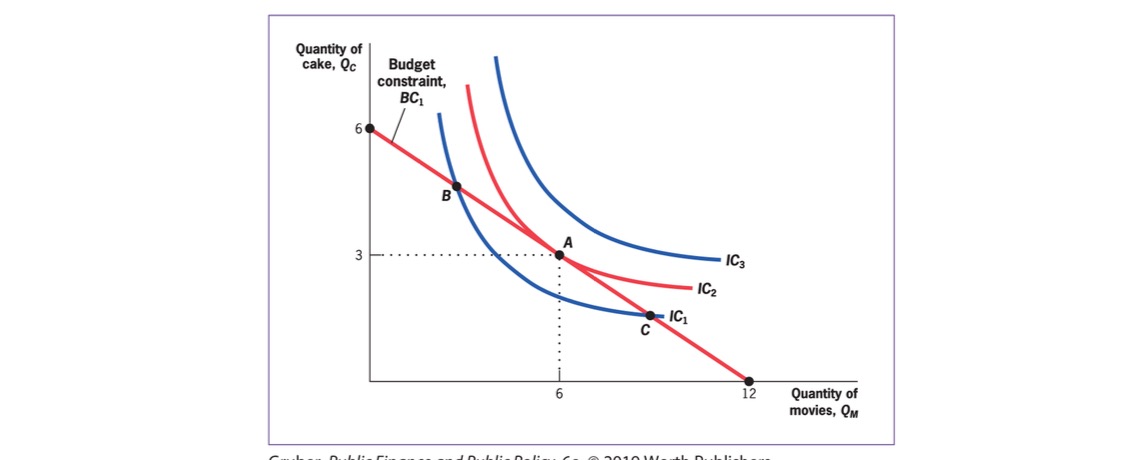
Indifference Curve: graphical Representation of bundles of goods that make qually well off

Underlying math: Utility Function

\[ U(Q_C.Q_M) = \sqrt{Q_C \times Q_M} \]

  • marginal utility = derivative, additional utility of one more

  • Diminishing Marginal Utility

Marginal Rate of Subst.: Willingness to trade one good for another, slope of IDC

Budget Constraint: $\( Y = P_C Q_C+P_MQ_M \)$

img

Price Changes#

can have two effects

  • Substitution Effect

  • Income Effect

Elasticity of Demand: % change in demand due to 1% increase in price

\[ e = \frac{ \frac{ \Delta Q }{Q} }{\frac{ \Delta P }{P}} \]

Supply#

Supply Curve = outcome of profit maximization

Production Function: \(q = \sqrt{K * L}\)

  • K = Capital

  • L = Labour

Profit Maximization at short term: \(p = MC\)

Equilibrium#

at Demand = Supply

img

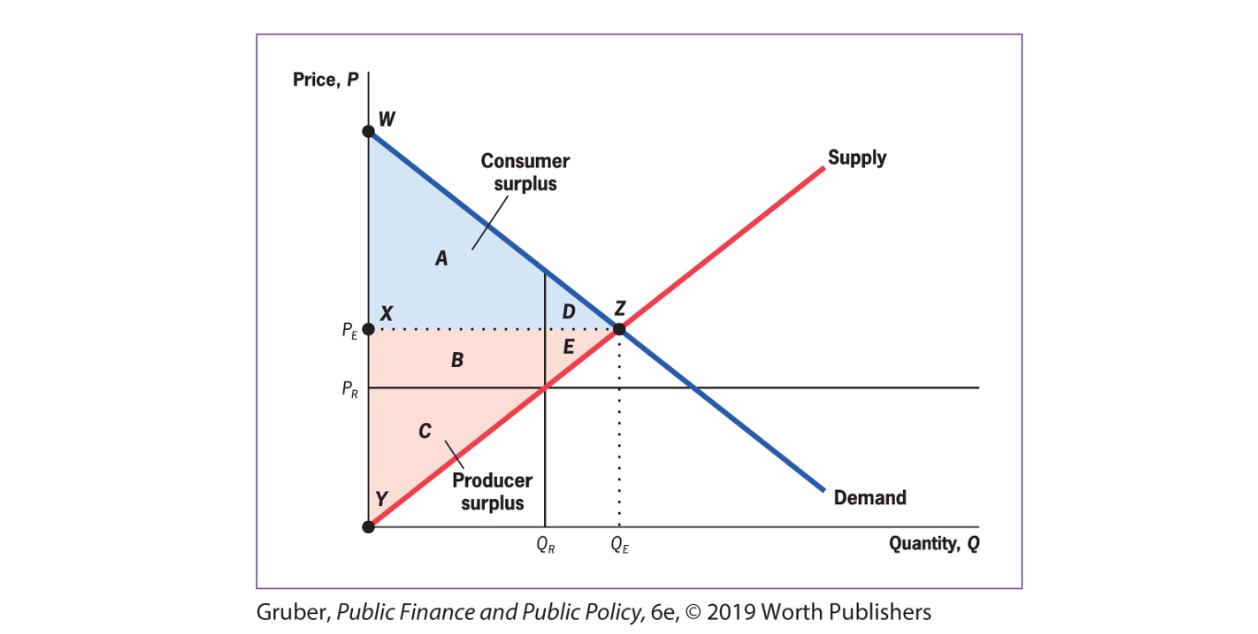
Theorems of Welfare Economics

  1. The competitive equilibrium, where supply equals demand, maximizes social efficiency.

  2. Society can attain any efficient outcome by suitably redistributing resources among individuals and then allowing them to trade freely.

under specific conditions!, that almost never exist (full information, no externalities?!)

Problem: Equity Effiency Tradeoff

Exercise#

2:#

\[ P = - \frac{ 1 }{10} Q+25 \]

Example Points:

  1. P=10 => Q=150

  2. P=5 => Q=200

Elasticity:

\[ e = \frac{ \frac{ \Delta Q }{Q} }{\frac{ \Delta P }{P}} = \frac{ \frac{ 50 }{150} }{\frac{ -5 }{10}} = \frac{ 1/3 }{-0.5}=-0.67 \]

Elasticity is only local (for these 2 points)

3: Subsidy#

Government subsidizes firts 5 units of clothing to half of price $\( 100 = 4*Q_F+10*Q_C \)$

now two slopes

  • \(p_{clothing} = 5\) for \(Q_C \le 5\)

  • \(p_{clothing} = 10\) for \(Q_C > 5\)

Clothing Intercept now = 12.5

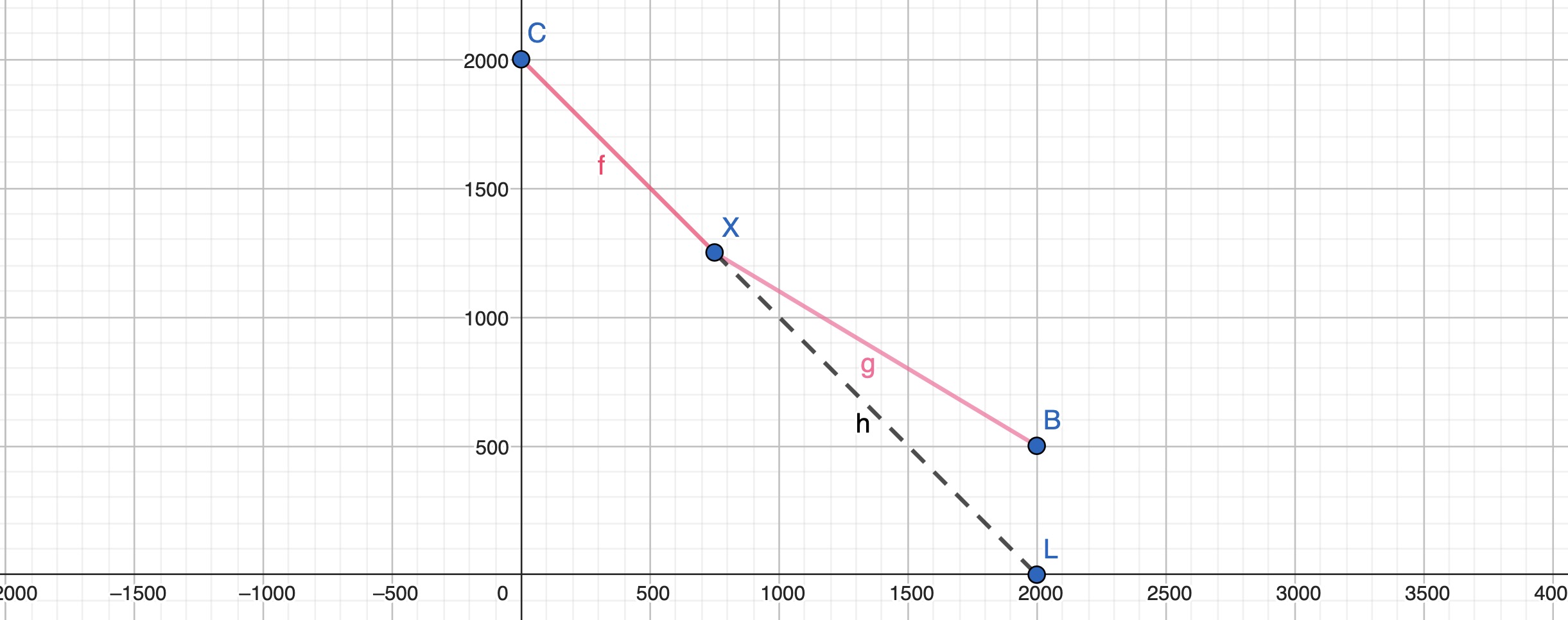
4: Income Program#

  • Work: 2000h at 10€

  • Benefit: 5000€

  • Benefit Reduction Rate = 40%

Kink Point (where you drop out of the program)

  • \(C*0,4 = 5000 \to C=12500\)

  • \(W=\frac{ 12500 }{10} = 1250\)

  • \(L=2000-1250 = 750\)

Graphic:

img