22.11.2021 Streuungsmaße#
Darstellung der Variationsbreite von Beobachtungen
immer positiv
einfache Streuungsmaße#
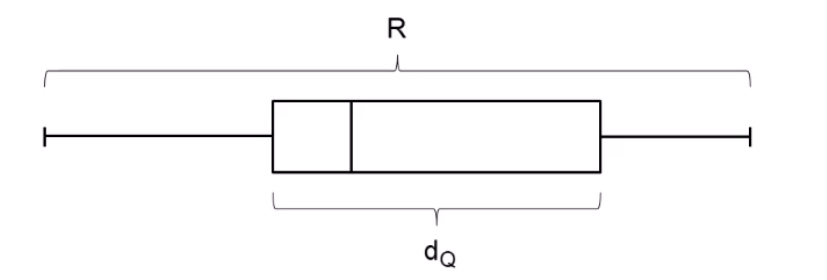
Spannweite (Gesamtbreite der Häufigkeitsverteilung): \(R = x_{ (n) } - x_{ (1) }\)
Interquartilabstand: \(d_Q = x_{0.75} - x_{0.25}\)
Streuungsmaße mit Lagebezug#
MAD#
Median der absolute Abweichung vom Median
MAD \( = med\{ |x_i - x_{med}|, i= 1,\dots,n \}\)
Standardabweichung#
Mittelwert der (quadrierten) Abweichung vom Mittelwert
Voraussetzung: kardinal skaliertes Merkmal X
Berechnung:
Abweichung von \(x_i\) von \(\bar{x}\) und ihr Quadrat \((x_i - \bar{x})^2\)
Mittelwert der Abweichung: \(\frac{1}{n} * \sum^n_{i=1} (x_i - \bar{x})^2 = \tilde{s}^2\) =
VarianzQuadratwurzel aus Varianz: \(\sqrt{ \tilde{s}^2 }\) =
Standardabweichung
vereinfachte Berechnung mithilfe von Verschiebungssatz (Formel S.8) = \(\left( \frac{1}{n} \sum^n_{i=1} x_i^2 \right) - \bar{x}^2\)
Variationskoeffizient#
unabhängig von Maßstab / Einheiten
Berechnung: \(v = \frac{\tilde{s}_x}{\bar{x}}\) (mit \(\bar{x}\) > 0)
Verhalten bei Transformation#
Ausgangssituation mit Werten \(x_i\) und Transformation mit \(y_i = a * x_i + b\)
Dann:
Das additive b ist unwichtig (weil nur Verschiebung)
Varianz: \(\tilde{s}_y^2 = a^2 * \tilde{s}^2_x\)
Standardabweichung: \(\tilde{s}_y = |a| * \tilde{s}_x\)
z-Standardisierung#
spezielle Transformation bei Kenntnis besonderer Kenngrößen
Berechnung: \(z_i = \frac{x_1 - \bar{x}}{\tilde{s}_x }\)
Folge: \(\bar{z}\) = Mittelwert = 0 ; \(\tilde{s}^2_z\) = Standardabweichung = 1
#
Schwankungsbereiche#
Arithm. MIttel + Standardabweichung = Konstruktion von Schwankungsbereichen
Intervall: \(\bar{x} \pm 1*\tilde{s}\) enthält 68% aller Beobachtungen
Intervall: \(\bar{x} \pm 2*\tilde{s}\) enthält 95% aller Beobachtungen
Intervall: \(\bar{x} \pm 3*\tilde{s}\) enthält 99% aller Beobachtungen