08.06.2024 Binary Variables#

Single Dummy Variable#

Binary Variable: represent qualitative factors in TRUE/FALSE format

Notation

\[\begin{split} female = \begin{cases} 1 \text{ if person is female}\\ 0 \text{ otherwise} \end {cases} \end{split}\]

Interpretation:

\[ wage = \beta_0 + \delta_0 female + \beta_1 educ + u \]

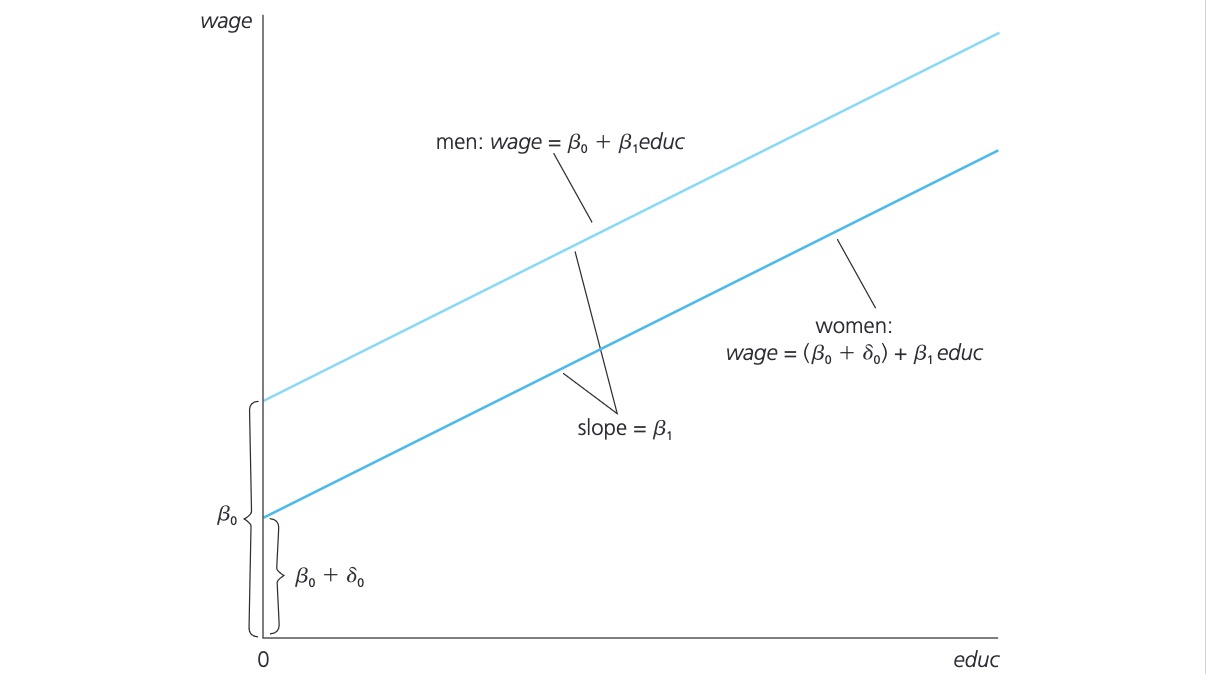
  • \(\delta_0\) = difference in wage between men and women (c.p)

  • \(\delta < 0\): women earn less

Representation:

img

Log Interpretation of Dummy Variables, e.g \(\ln wage = female + educ + exper\)

  • Roundabout: like a normal estimate: \(100 \cdot \delta\)

  • exact: \(100 \cdot [exp(\delta) - 1]\)

Dummies for multiple categories#

e.g. Model for wage differences across groups (married men, married women, single men, …)

  • create dummies for each (marrmale, marrfem, singfem)

  • base group = single males (have 0 and 0 on both categories)

Difference between single women and married women? Reestimate

Alternative: Interactions

e.g:

\[ \ln wage = .321 - .110 female + .213 married - \bold{.301 female \cdot married} + u \]

  • single men: female=0, married=0

  • married men: female=0, married=1 => \(.321+.213 = 0.534\)

Binary as dependent variable#

a.k.a linear probability model

  • Try to explain the binary outcome

  • e.g. college student using drugs in given school year

\[ P(y=1|x) = \beta_0 + \beta_1 x_1 + ... + \beta_k x_k \]

Example: Wome working outside home (labor force participation)

\[ \widehat{lfp} = .586 - .0034 nwifeinc + .038 educ + .039 exper + ... \]

  • another yerar of education = increase probability by 0.038

  • 10 years = 10(0.038) = 0.38

Note:

  • LPM is always heteroskedastic

  • caution with standard errors