18.10.21 Matrizen Weiterführung + Linear#
Erkenntnis aus der Assoziativität:
Gleiches Ergebnis
Unterschiedlicher Arbeitsaufwand !
Transponieren#
\((AB)^T = B^T A^T\)

Nullteiler:

Rechenbeispiel
Wir nehmen jetzt an, dass aus Rohstoffen/Ressourcen y zunächst Zwischenprodukte z hergestellt werden. In einem zweiten Schritt werden daraus, und unter Verwendung weiterer Ressourcen, Endprodukte x gefertigt. Wie viele Ressourcen y sind für die Produktion von x einzusetzen?

Linearkombinationen#
Definition: Seien v, i = 1,…,m Vektoren in R^n.
Dann= \(a_1v_1 + ... + a_mv_m\) = Linearkombination
Menge aller Linearkombinationen= linearer Raum

eine Menge M heißt linearer Raum, wenn M bezüglich Addition + Multiplikation mit einem Skalar abgeschlossen ist
linear abhängig: Menge von Vektoren, wenn eine Menge von a1,a2,… existiert, dass Resultat (0,0,…,0)^T ist
einen Vektor kann man durch die Anderen beschreiben
Basis: Menge \( B \in M \) (linearer Raum) = kleinstmögliche Anzahl an Vektoren zur Beschreibung
Vektoren der B sind linear unabhängig
Standard-Einheitsvektor = kanonische Basis
Gaußsches Eliminationsverfahren#
Beispiel eines Linearen Raumes:

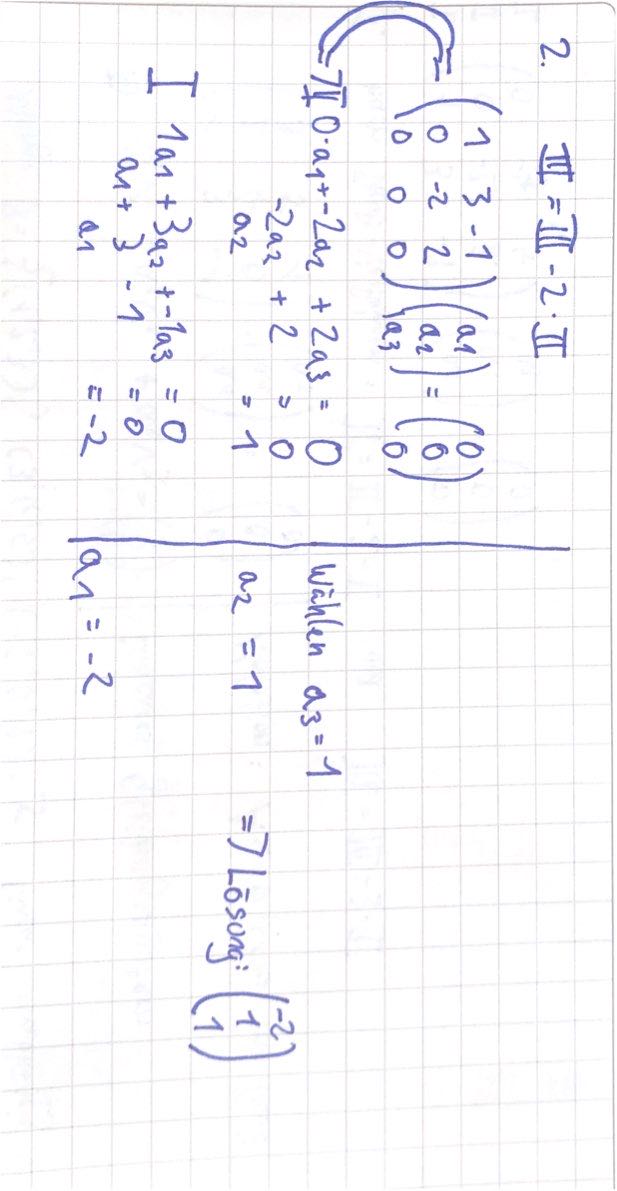
Schritte:
Transformieren der matrix in Stufenform durch Addition von Vielfachen von Zeilen auf Andere
Rücksubstitution: Löse das System in Stufenform
Rang: Anzahl Zeilen linear unabhängig in einer Matrix (nicht nur Nullen) = Anzahl Stufen