15.12.2022 Intertemporale Entscheidungen#
Intertemporale Entscheidungen: Entscheidungen, in denen Zeitunterschiede relevant sind, weil Nutzen und Kosten in unterschiedlichen Perioden
Beispiel Handyversicherung / Sparen
= Entscheidung zw. Konsum heute <–> Konsum Zukunft
Exponentielles Diskontieren#
gängiges Modell von Samuelson 1937
Zeitperioden t=0,1,…
Nutzenstrom \(\bold{u} = (u_0,u_1,...,u_\infty)\)
Nutzen aus Nutzenstrom: \(U^0( \bold{u})\)
Entscheider:innen wählen max U
Zeitpräferenzen#
Entscheidung zw. 100€ morgen <–> 100€ heute (präferiert)
Nutzenerhöhung zwischen Zeiten = individuelle Zeitpräferenz
messen mit Diskontfaktor \(\delta \in (0,1)\)
heutiges Geld wird mit Diskontfaktor für Nutzen in nächster Periode multipliziert
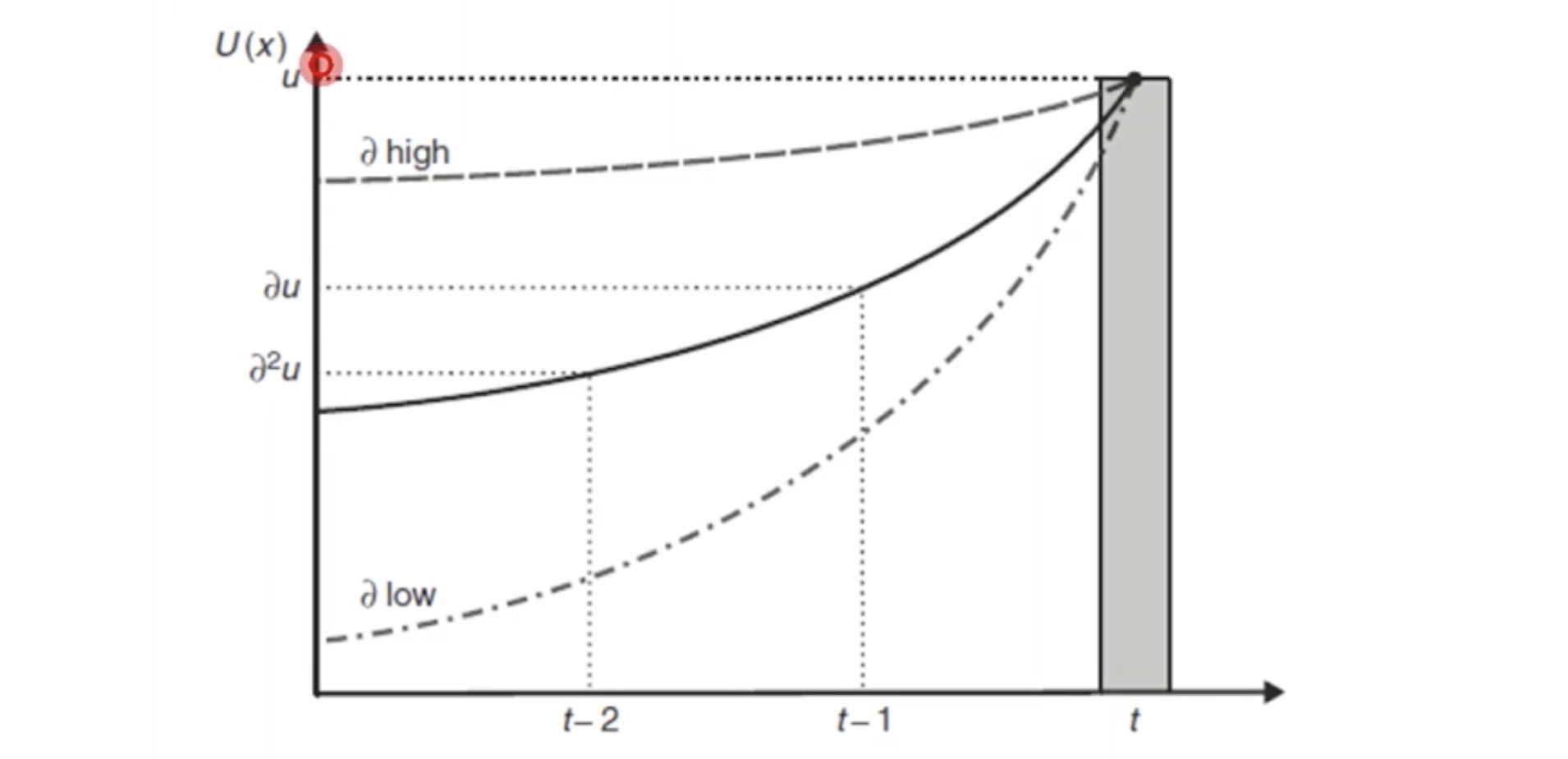
Nutzen 100€ übermorgen bekommen aus heutiger Sicht $\( \underbrace{\delta \delta u}_{\text{übermorgen 100}} = \underbrace{\delta ^2 u}_{\text{heute 100 übermorgen}} < \underbrace{\delta u}_{\text{heute 100 morgen}} < \underbrace{u}_{\text{heute 100}} \)$
Beispiel Alternativen a bis d
t=0 |
t=1 |
t=2 |
Nutzen mit \(\delta\)=0.9 zu t=0 |
\(\delta=0.1\) |
|
|---|---|---|---|---|---|
a |
1 |
0 |
0 |
1 |
1 |
b |
0 |
3 |
0 |
\(3 * 0.9 = 2,7\) |
0,3 |
c |
0 |
0 |
4 |
\(4 * 0.9^2 = 3,24\) |
0,04 |
d |
1 |
3 |
4 |
\(1+3 * 0.94 +4* 0.9^2 = 6.94\) |
1,34 |
Hohes \(\delta\) = geduldig, bereitschaft zu verzicht (gute Studis)
niedriges \(\delta\) = ungeduldig, keine Bereitschaft (Raucher)
Alternativ: Diskontrate r = \(\frac{1-\delta}{\delta}\)
\(\delta = 1 \to r=0\): Zukunft nicht abgezinst
\(\lim_{\delta \to 0} \to r = 1\): Zukunft komplett abgezinst
Implizite Annahmen#
Präferenzen sind zeitkonsistent
Nur Barwert des Nutzens relevant
Zeitkonsistenz: Entscheidungen zw. 2 Situation (a,b) in jeder Periode gleich
$\(
U^t(a) > U^t(b) \Longleftrightarrow U^{t+1}(a) > U^{t+1}(b) \newline
U^t(a) < U^t(b)\Longleftrightarrow U^{t-1}(a) < U^{t-1}(b)
\)$
Grafik: 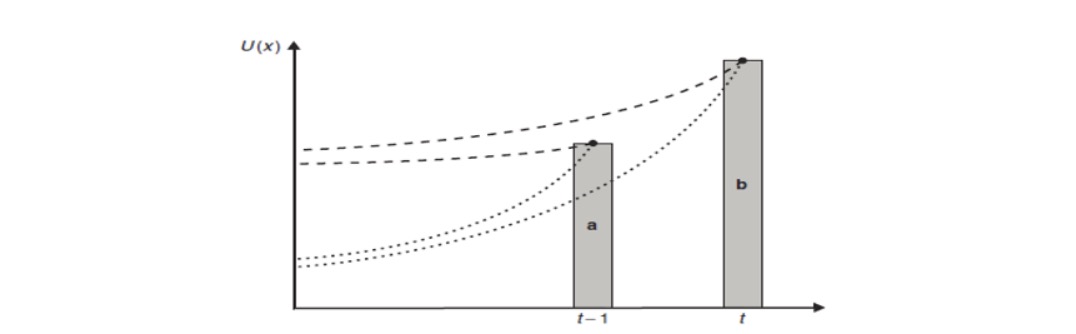
entweder a>b (Punkte)
oder a<b (Strichel)
kein Schneiden der Linien!