01.05.2022 Dichte und Lageparameter

für stetige Zufallsvariable

• Wertebereich \(X(\Omega)= \R\)

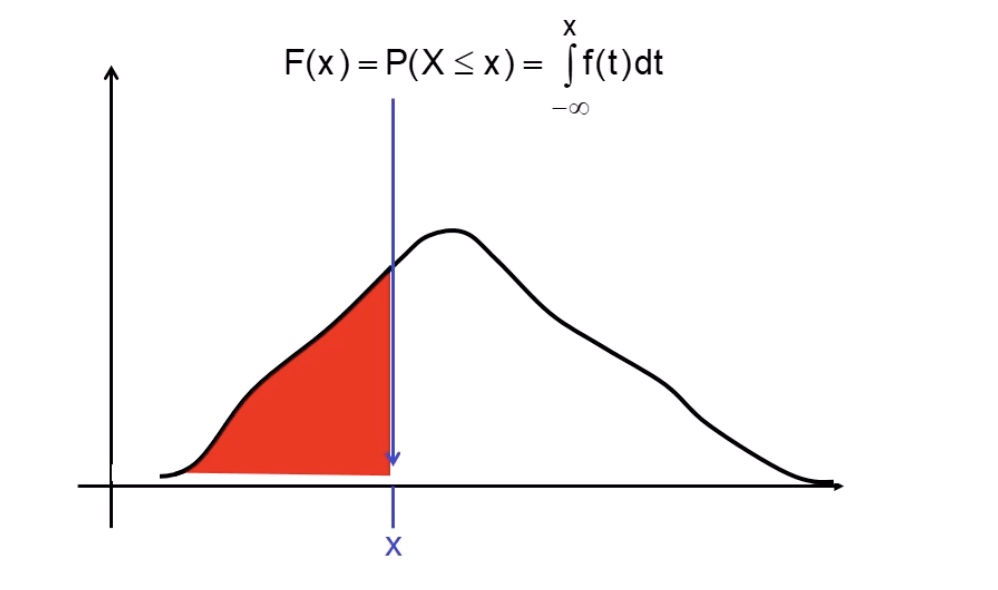
• Definition: \(P(X \le x) = F(x) = \int_{-\infty}^x f(t)dt\)

  • Fläche unter der Kurve die bis Funktionswert x ist

• es gilt: \(f(x) \ge 0 \ \forall x;\ \int_{-\infty}^\infty f(t)dt=1\)

  • die gesamte Fläche der Kurve ergibt 1 = 100 %

Beispiel

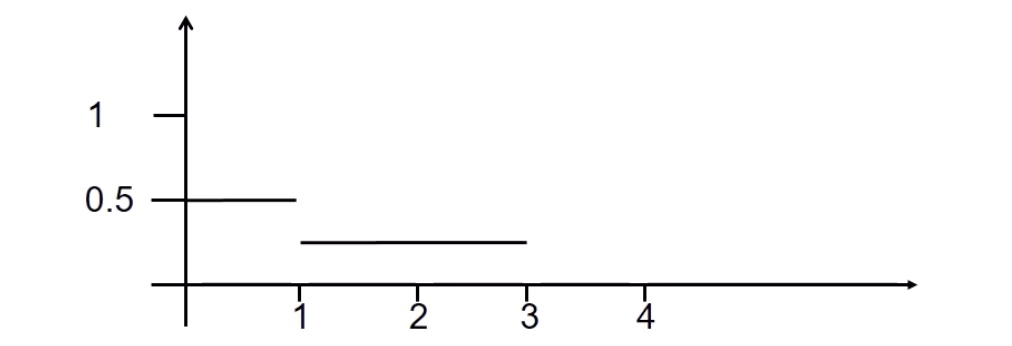
Betrachtete Funktion: $$ f(x) =

\left{\begin{array} 00.5 & 0\le x\le 1 \ 0.25 & 1 < x \le 3 \ 0 & \text{sonst} \end{array}\right. $$

• nicht mathematisch stetig

• Bedingung für Funktionen !

  • [x] Werte > 0

  • [x] \(\int_{-\infty}^\infty f(t)dt = 1\)

anhand einfacher Lageparameter erfassbar:

Modus

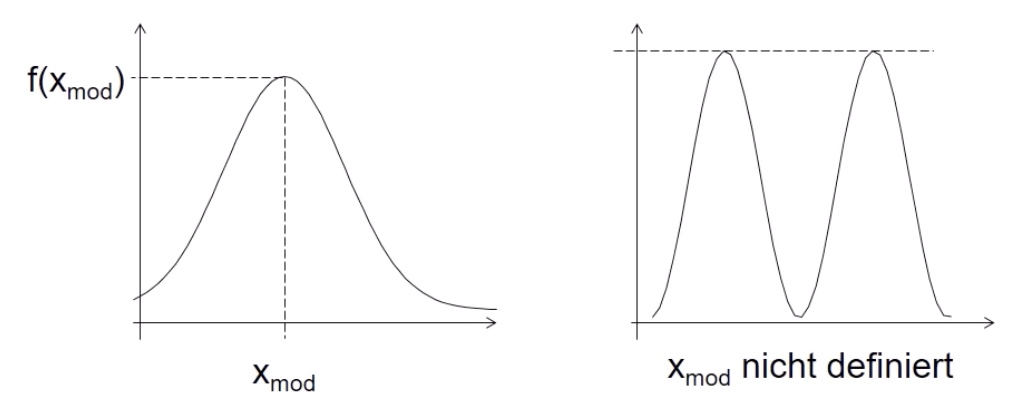
Definition: x-Wert, bei dem f(x) maximal

• bei zwei gleichen Werten = undefiniert

Erwartungswert

Gegenstück zum arithmetischen Mittel bei diskretem X

Definition: $\( E(x) =\int_{-\infty}^\infty x * f(x)dx \)$

• kann auch nicht existieren

• Transformationsfest: \(Y = a*X+b \to E(Y) = a*E(x)+b\)

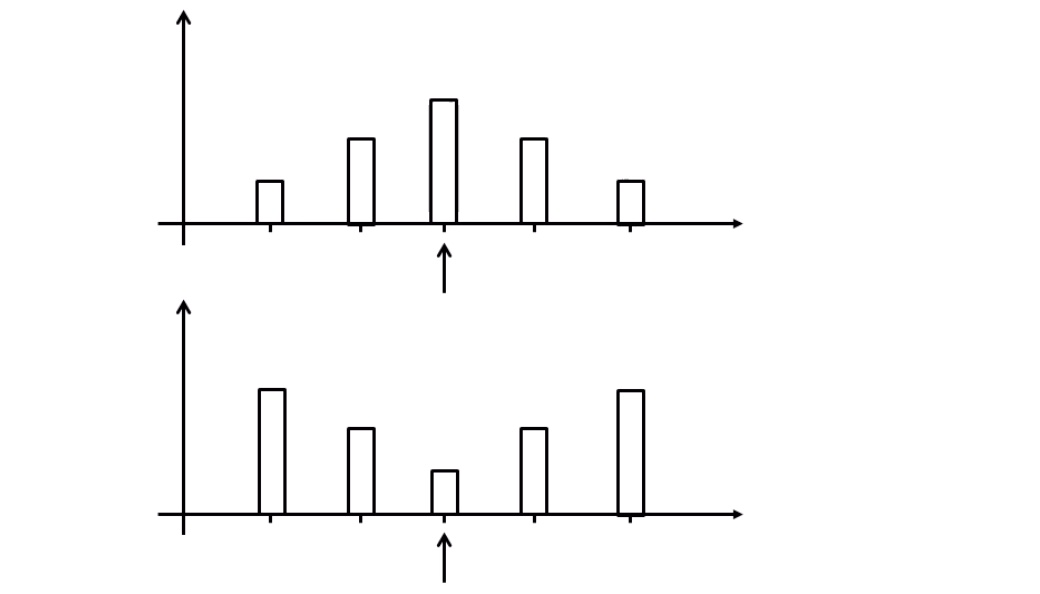
• Erwartungswert ist Schwerpunkt / Symmetriestelle (bei symmetrischer Funktion)

Beispiel

• Alle 6 Minuten kommt Straßenbahn, wie lange muss ich wahrscheinlich warten wenn ich irgendwann losgehe?

Bestimmung des Erwartungswertes mit Integralen $\( \begin{aligned} E(x) &= \int_{-\infty}^\infty x * f(x)dx \\ &= \int_0^6 x * \frac{1}{6}dx \\ &= \frac{1}{6}*\Big( \frac{1}{2}* x^2\Big)\bigg|_0^6 \\ &= \frac{1}{12}*(36-0) = \frac{36}{12} = 3 \end{aligned} \)$ graphische Darstellung: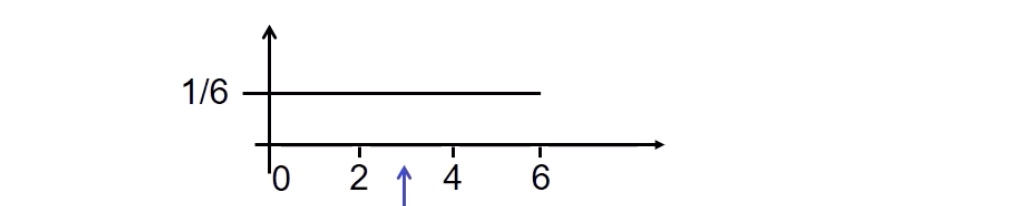

• auch Argumentation mit Symmetriestelle möglich

p-Quantil

für stetige Zufallsvariable: $\( \text{Definition: }\underbrace{P(X < x_p)}_{F(x_p)} = p \)\( für diskrete Zufallsvariable: \)\( P(X < x_p) \le p \text{ und } P(X > x_p) \le 1-p \)$

• Stelle suchen, dass unter/ oberhalb von Stelle Wahrscheinlichkeit kleiner / größer