10.01.2022 Korrelation

Bestimmung des Zusammenhangs für höher skalierte Werte als die nominalen

Pearsons Korrelationskoeffizient

für metrische Merkmale!

2 Merkmale X,Y mit Paaren \((x_1,y_1), ...,(x_n,y_n)\),

Berechnung: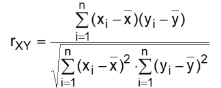

Wertebereich: \(-1 \le r_{XY} \le 1\) ,

• \(|r_{XY}|\) = Zusammenhang

• Einteilung wie bei \(K^*\) (stark, schwach,…)

• Vorzeichen => Richtung des Zusammenhangs

alternative Berechnung: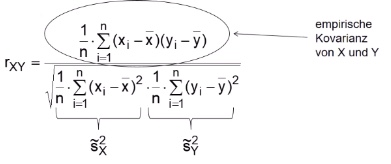

Beispiel

Prognoziertes Wachstum (X) vs reales Wachstum (Y)

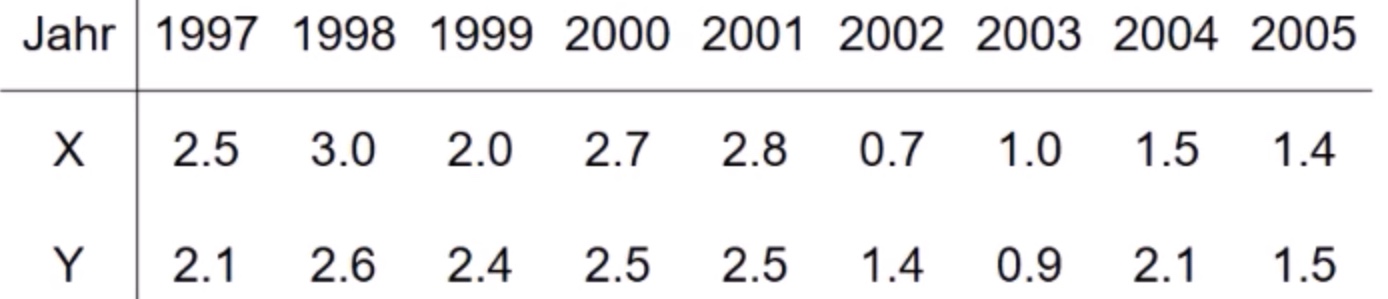
Darstellung im Streudiagramm:

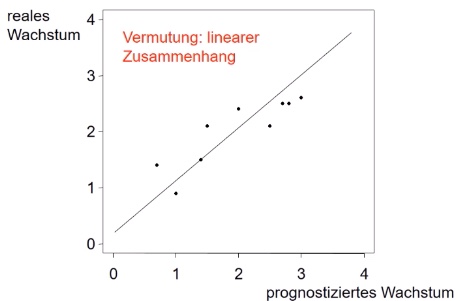
Berechneter Korrelationskoeffizient ~0.87 = stark

Rangkorrelation

für ordinale Merkmale

Beispiel: Beliebtheit von 5 Politikern

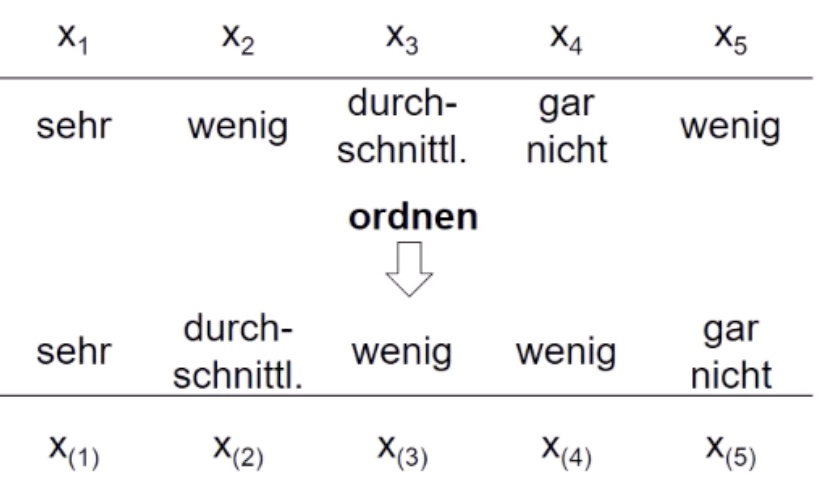
Problem: die beiden wenigs haben keine exakte Bindung

Lösung: beide die Mitte = 3.5 nehmen! (Mittelrangbildung)

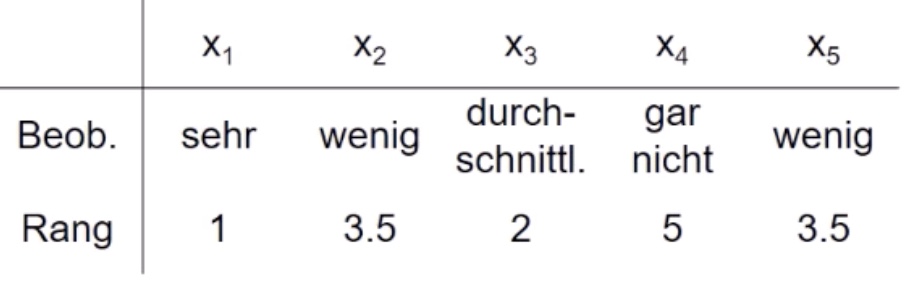
Rangkorrelationskoeffizient

• Wertebereich \(-1 \le r_{sp} \le 1\)

• Messung der Monotonie

• Zusammenhangstärke : \(|r_{sp}|\)

• vereinfachte Version, wenn keine Bindungen (Formelsammlung)

aus Pearson abgeleitet, aber mit Ränge statt Werte $\( r_\text{Sp} = \frac{\sum_{i=1}^n (\text{rang}(x_i) – \overline{\text{rang}(x)}) (\text{rang}(y_i) – \overline{\text{rang}(y)})}{ \sqrt{\sum_{i=1}^n (\text{rang}(x_i) – \overline{\text{rang}(x)})^2} \cdot \sqrt{\sum_{i=1}^n (\text{rang}(y_i) – \overline{\text{rang}(y)})^2} } \)$ Vereinfachung: Rangmittelwerte bilden

• \(\overline{\text{rang}(y)} = \overline{\text{rang}(x)}= \frac{n+1}{2}\)

Vereinfachter Spearman-Koeffizient:

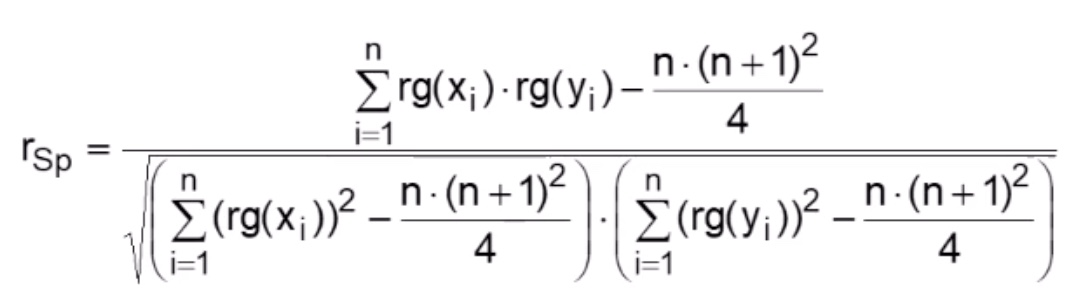
Interpretation der Korrelation

• keine Wirkrichtung, sondern wechselseitiger Zusammenhang

• Korrelation ≠ Kausalität

• Richtung des Zusammenhangs -> bei mind. ordinalen Merkmalen

• für Ursache-Wirkung: Regression!