24.01.2022 Transportproblem 2#

Beispiel 161 f.#

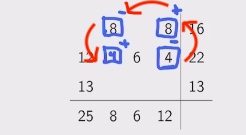
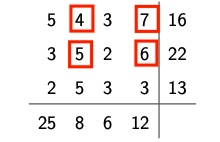
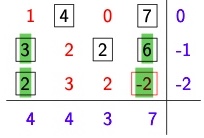
links Mengentableau X, rechts Kostentableau C

22-01-24_17-39

Transportkosten : \(z = 186\)

  • Frage: was passiert, wenn wir \(x_{24}\) um 4 senken

  • muss \(x_{14}\) Um 4 erhöhen; \(x_{12}\) Um 4 verringern; \(x_{22}\) um 4 erhöhen

=> Kreisförmig ausgebreitet = Austauschkreis

Mengen

Kosten

22-01-24_17-47

22-01-24_17-51
\[\begin{split} \textbf{Entstehende Kosten} \\ \begin{aligned} \triangle z : -4*6+4*7-4*4+4*5 =\\ 4 * (-6+7-4+5) = \\ \text{relativer Preis} = 2 \end{aligned} \end{split}\]

MIDI-Algorithmus#

Schritt

Anwendung

Darstellung

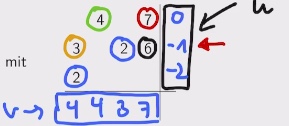
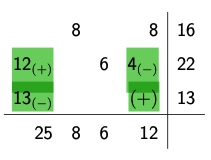
1. setze \(u_1 = 0\) und bestimme \(u_2,...,u_n\) und \(v_1,...,v_n\)

\(u_1 = 0\) Gesetzt, dann \(v_4=7\) eingetragen da 7+0 = 7 (rotes Kombielement)

22-01-24_18-20

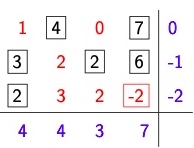
2. Bilde \(\triangle_{ij} = c_{ij}- u_i - v_j\)

\(\triangle_{2,4} = 6-7-u_2 \to u_2 = -1\) und so weiter für alle Felder

22-01-24_18-23

3.wenn alle \(\triangle_{ij} \ge0 \to\) Optimal

wenn nicht => IV

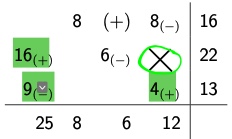
4a. Austauschkreis finden mithilfe eines Rechtecks

Der Kreis besteht aus Elementen \( (2,1); (2,4), (3,1); (3,4)\)

22-01-24_18-39

4b. zugehörige Verschiebung \(d\) finden

Verschiebung = anzahl Austausch: in Mengentableau niedrigstes Element des Kreises = 4

22-01-24_18-42

4c. alle Elemente des Austauschkreises um \(d\) Verringern/ erhöhen

bei jedem Plus \(12 +4 = 16\)

22-01-24_18-49

4d. wenn nicht optimal, alles wieder von vorne (Schritt 1)

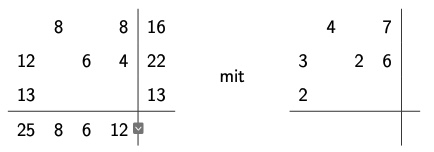
Beispiel 161 Fortsetzung#

BSP 161

=> komplete Lösung im Skript nachvollziehbar