10.01.2022 Wiederholung + Dualität#
Wiederholung#
Lineares Optimierungsproblem (LOP): System von Gleichungen und Ungleichungen
besteht aus:
Vorzeichen-Bedingung
Bsp.: \(x_1,x_2 \ge 0\)
Nebenbedingungen
\(3x_1 - x_2 \le 2\)
Umformung \(*-1: -3 x_1 + x_2 \le 2\)
Zielfunktion
\(-3 x_1 + 4x_2 = min!\)
Umgeformt \(*(-1): 3x_1 + 4 x_2 = max!\)
Lösung der LOPs: Simplexalgorithmus
einfach mit: Standardmaximumproblem
VZ: \(... \ge 0\)
NB: \(Ax \le b\)
ZF: \(... = max!\)
und \(b \ge 0\) (alle Komponenten des Vektors b)
sonst Umformung und schwierige Bestimmung der Anfangsecke
Dualität#
anhand Einführungsbeispiel mit Ausgangstoffen \(R_1,R_2\) und Endprodukten \(E_1,E_2,E_3\)

Primalproblem#
VZ: \(R_1,R_2 \ge 0\)
NB: (Lieferverpflichtungen)
\(0.2 R_1+0.5R_2 \ge 6 E_1\)
\(0.4R_1 + 0.25 R_2 \ge 10 E_2\)
\(0.3 R_1+0.1 R_2 \ge 3 E_3\)
ZF: \(25 R_1+20R_2 = min!\)
Dualproblem#
Alternativ: Einkauf von Endprodukten: bis zu welchem Preis ist das sinnvoll?
Variablen sind Preise von \(E_1,E_2,E_3\) : \(y_1,y_2,y_3\)
VZ: \(y_1,y_2,y_3 \ge 0\) (logisch)
ZF: anhand der obigen Lieferverpflichtungen der Produkte
bspw. \(6 E_1\) zum Preis von \(y_1\)
\(ZF = 6y_1+10y_2+3y_3\)
NB: die Preise sollen niedriger sein als bei eigener Produktion
\(0.2y_1+0.4y_2+0.3y_3 \le 25\)
Erklärung: Beispiel Verteilung von Rohstoff \(R_1\) auf Endprodukte inklusive Preis (25GE/ME)
\(0.5 y_1+0.25 y_2+0.1 y_3 \le 20\)
Zusammenhänge#
Nebenbedingungen |
Zielfunktion |
Vorzeichen |
|
|---|---|---|---|
Primal |
\(Ax \ge b\) |
\(c^Tx = min\) |
\(x\ge 0\) |
Dual |
\(A^Ty \le c\) |
\(b^Ty = max\) |
\(y \ge 0\) |
Beispiel 144#
Beispiel mit Produkten \(x_1, x_2\) und Maschinen \(y_1 , y_2 , y_3\)
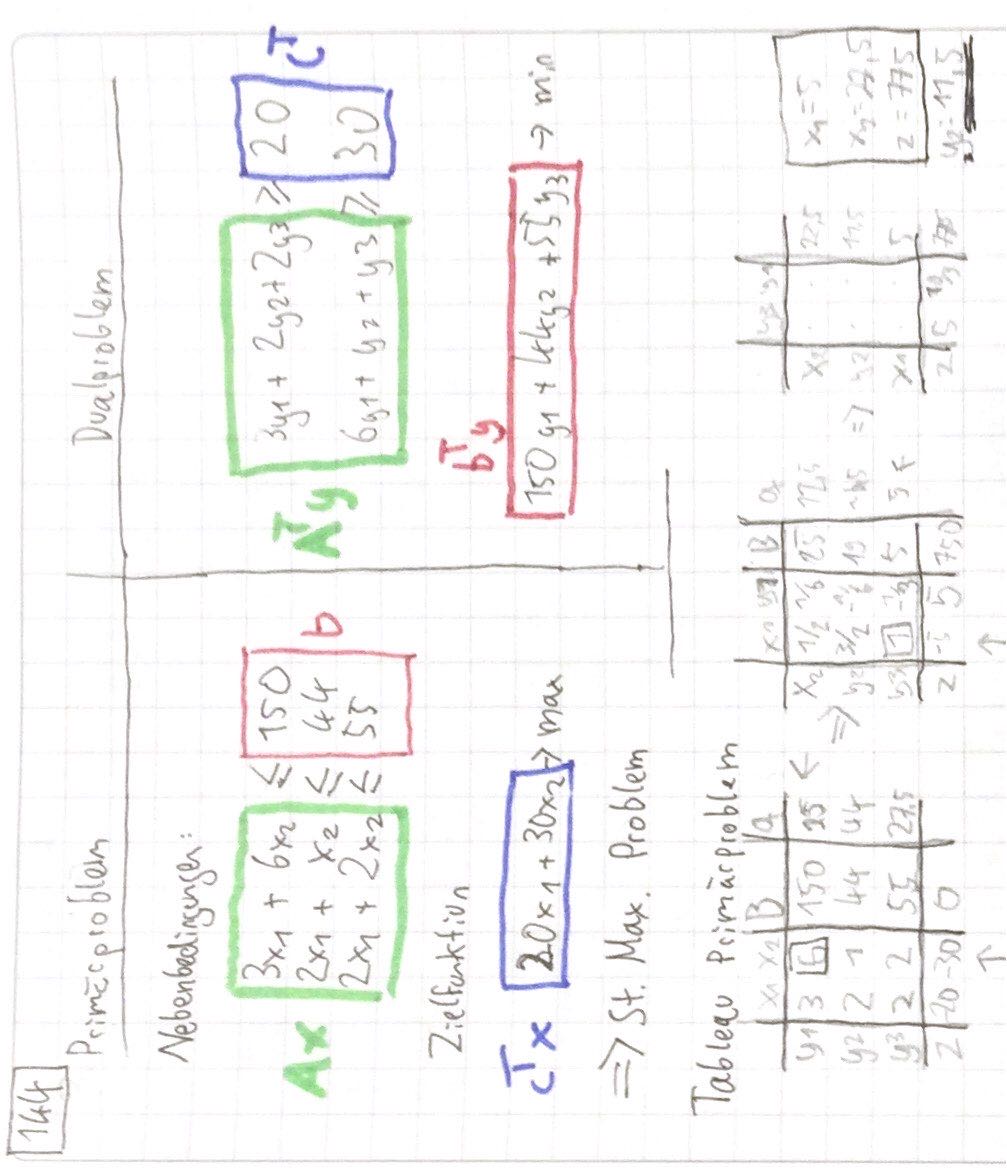
da \(y_2 \neq 0\), heißt, es gibt hier „kostenlose Kapazität“ , die man noch vermieten könnte, ohne Profit zu schmälern
die anderen Maschinen sind vollausgelastet!
Optimallösung aus unterster Zeile z: $\( 5 y_3 + 10/3 y_1 + z = 775 \\ \to z = 775 - 5 y_3 - 10/3 y_1 \)\( => Bei Vermietung aller Maschinen fällt Profit (775) um je \)u_1^* = 10/3\( , \)u_3^* = 5\( un \)u_2 = 0$
\(u_1, u_2, u_3\) sind Schattenpreise / Opportunitätskosten und Mindestpreise der Vermietung, und werden Dualvariablen!