08.11.2021 Eigenwerte#

Eigenwerte#

Eigenwerte EW: \(\lambda\) wenn \(Av = \lambda v \) mit \(v \neq 0\)

Berechnung (Beispiel 82): \( A = \left(\begin{array}{rrr} 0 & 1 \\ 1 & 0 \\ \end{array}\right) \) $$ Eigenwerte \ det (A - \lambda I) = det(\begin{array}{rrr} -y & 1 \ 1 & -y \ \end{array}) = 0 \ = -y^2 -1*1 = 0\implies y_1 = 1; y_2 = -1 \

Eigenvektor: \ (A-\lambda I ) v = 0\ y_1 = 1: \left(\begin{array}{rrr} 1 & -1 \ -1 & 1 \ \end{array}\right) \left(\begin{array}{rrr} x \y \end{array}\right) = \left(\begin{array}{rrr} 0 \0 \end{array}\right) \ \implies wenn \ x=y \ loesbar = v_1 = (1,1)^T\

y_2 = -1 : \left(\begin{array}{rrr} 1 & 1 \ 1 & 1 \ \end{array}\right) \left(\begin{array}{rrr} x \y \end{array}\right) = \left(\begin{array}{rrr} 0 \0 \end{array}\right)\ \implies wenn \ x = -y \ loesbar = v_1 = (1,1)^T $$

Bemerkung: wenn \(\lambda\) Eigenwert der reellen Matrix, dann auch \(\bar{\lambda}\)

Beispiel 85: Eigenwerte

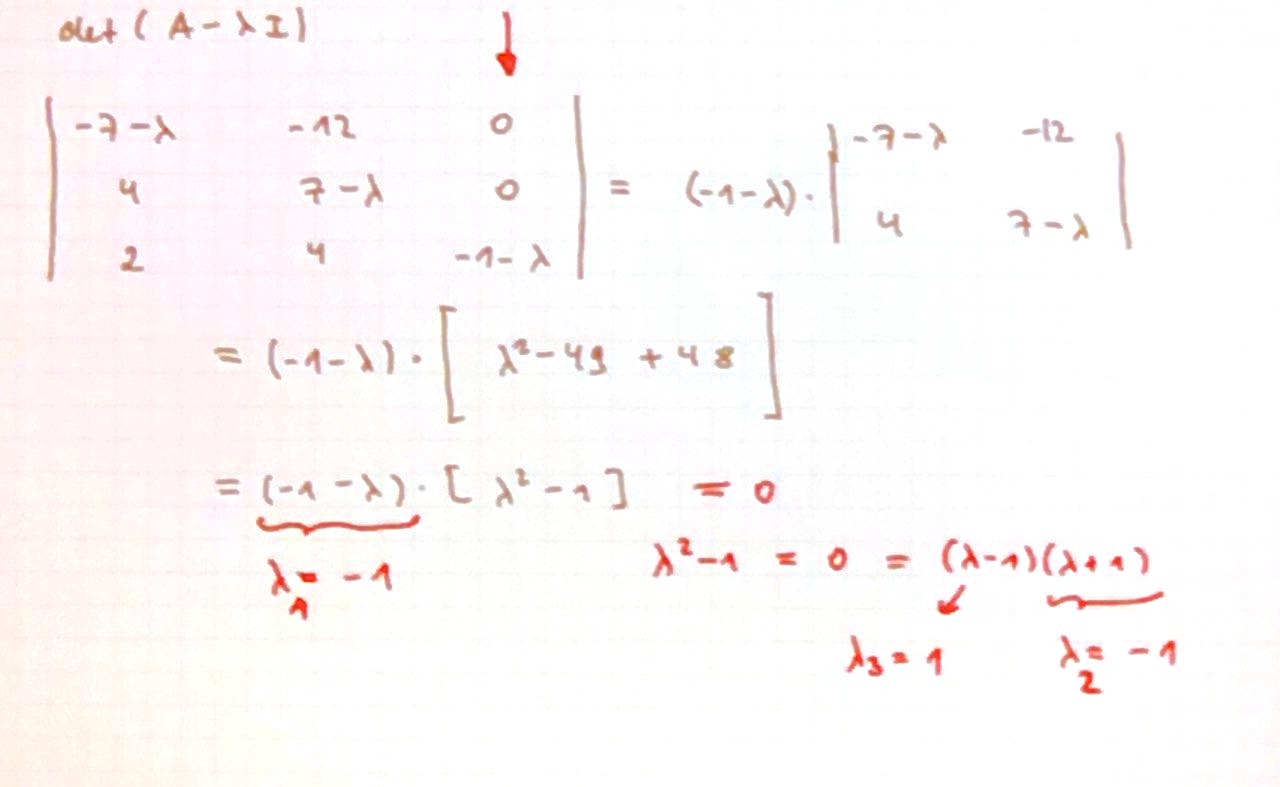
21-11-08-13-58-13

Eigenvektoren: 21-11-08_14-04

Besetzen der Matrix mit Vektoren und dann invertieren $\( A = \left(\begin{array}{rrr} 0 & -2 & -3 \\ 0 & 1 & 2\\ 1 & 0 & 1 \end{array}\right) \implies A^{-1} = \left(\begin{array}{rrr} -1 & -2 & 1 \\ -2 & -3 & 0\\ 1 & 2 & 0 \end{array}\right) \)$

Eigenschaften der Eigenwerte (EW):

  • Eigenwert von A = Eigenwert von \(A^T\) , aber nicht gleiche Eigenvektoren!

  • Eigenwert von Diagonalmatrizen = Diagonaleinträge

  • EW von \(A\) = EW von \(V^{-1}AV\)

  • A ist invertierter, wenn alle Eigenwerte nicht null !

  • EW von \(A^{-1}\) = \(\frac{1}{EW} \) von A

  • symmetrische Matrix: Eigenwerte reell