20.06.2022 Tests 2#

Ablauf eines Tests#

Testproblem mit 2 Thesen $H_0$ und $H_1$
Signifikanzniveau $\alpha$, meist 0.01, 0.05, 0.1
Zufallsstichprobe
Berechnung Teststatistik
Entscheidungsregel anwenden

Beispiel: sind Brötchen vom Bäcker zu leicht (weniger als 50g)?

Brötchengewicht X
Annahme $X \sim N(\mu, \sigma^2)$, hier $\sigma^2 = 1.44$
Behauptung Bäcker: $\mu = 50$
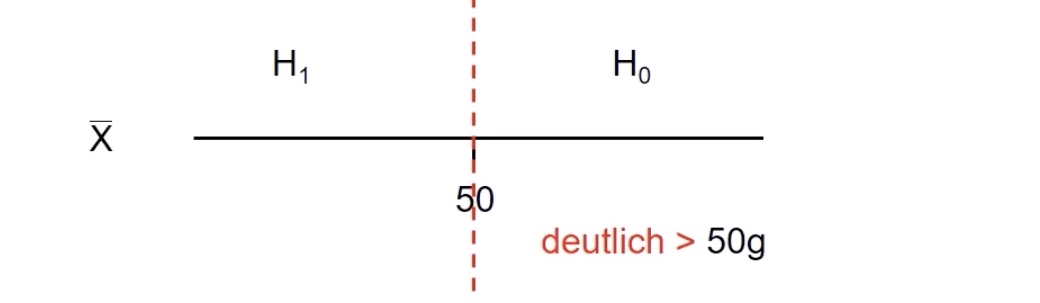
$H_0: \mu \ge 50$ (zufrieden) vs. $H_1: \mu < 50$ (unzufrieden)

statistische Modellierung:

Kunde zieht Stichprobe vom Umfang n: $X_1, ...,X_n$
$\bar{X}$ = Durchschnittsgewicht = Prüfgröße

2022-06-22_11.29.20

Hypothesentests#

mit $\mu$ der zu überprüfende Wert und $\mu_0$ der ausgesagte Wert

Test	Hypothese $H_1$	Gegenhypothese $H_1$	$H_0$ Ablehnen, falls
linksseitig	$\mu \ge \mu_0$	$\mu < \mu_0$	$\sqrt{n}\cdot\bigg
rechtsseitig	$\mu \le \mu_0$	$\mu > \mu_0$	$\sqrt{n}\cdot\frac{\bar{X}- \mu_0}{\sigma}< -z_{1-\alpha}$
Zweiseitig	$\mu = \mu_0$	$\mu \ne \mu_0$	$\sqrt{n}\cdot\frac{\bar{X}- \mu_0}{\sigma}> z_{1-\alpha}$

Beispiel linksseitige Hypothese: = Brötchenbeispiel

Bäcker sagt, dass seine Brötchen größer sind als 50g: $H_0: \mu \ge 50$
Verbraucher stellt Gegenthese, dass sie kleiner sind: $H_1: \mu < 50$

Beispiel: Schafft Partei A es in Landtag?

Hypothese: sie schafft die 5%-Hürde: $p \ge 0.05$
Gegenhypothese: $H_1: p < 0.05$

Wahlbefragung Stichprobe:

n=100
4 Wähler von A

Jetzt: Bernoulli-Test, nicht mehr normalverteilt! $$ X_i = \begin{cases} 1, &\text{wählt A}\\ \quad i-\text{ter Wähler}\\ 0 &\text{wählt nicht A} \end{cases} $$ Erfolgswahrscheinlichkeit p entspricht Stimmenanteil

und da Bernoulli eine Binomialverteilung: $$ X_i \sim Bin(1,p) $$ und Binomialverteilung erlaubt uns, anzunehmen, dass 4% der Menschen Partei A wählen

Test auf Unabhängigkeit zweier Merkmale#

Testproblem:

$H_0$: X, Y unabhängig vs. $H_1$: X, Y abhängig
X, Y kategorisiert mit k bzw m Kategorien

$H_0$ zum Niveau $\alpha$ verwerfen, falls $$ \chi^2 = \sum_{i=1}^k \sum_{i=1}^m \frac{(h_{ij}-e_{ij})^2}{e_{ij}} > \chi_{(k-1)(m-1);1-\alpha} $$

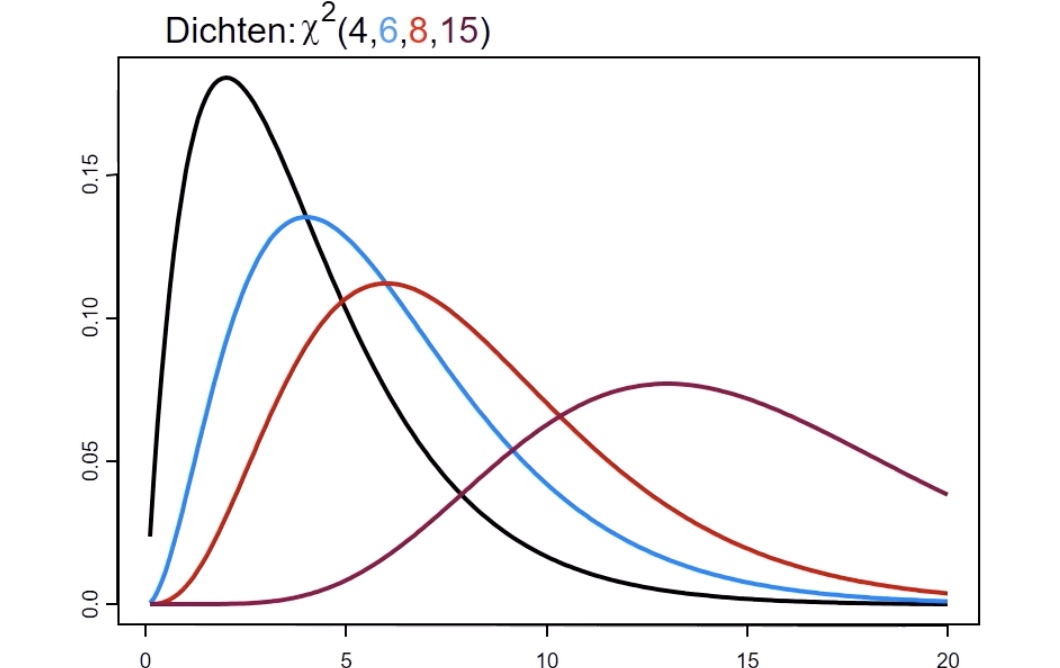
$\chi^2$-Verteilung (Chi-Quadrat)#

nicht symmetrisch
Parameter q = „Freiheitsgrade“
$X \sim \chi^2_q$
- E(X) = q
- Var(X) = 2q

2022-06-22_18.00.17

Ablauf des Tests#

Testproblem: $H_0$ Vs. $H_1$
Signifikanzniveau vorab wählen: $\alpha$
Teststatistik anhand Stichprobe berechnen
Entscheidungsregel: $H_0$ Verwerfen, falls …
Entscheidung

Besonderheiten:

interessierende Aufgabe als Gegenhypothese $H_1$ formulieren
- dann aktive Entscheidung für unsere Hypothese
- $H_1$ muss sich gegen $H_0$ durchsetzen

Beispiel#

Studie zu Kindeswohl in 29 Industrienationen

Deutschland: 84.1 % der Kinder sagen, es geht ihnen gut
- ist das gut für eine Industrienation?

Durchschnitt der Länder = 85.74 , Standardabweichung = 3.43

Konfidenzintervalle für deutschen Wert#

Annahme der Normalverteilung $X_i \sim N(\mu,\sigma^2)$

Formelsammlung 16.2 und sigma unbekannt (S.25): Konfidenzintervalle $$ \Big[\bar{X}- \frac{S}{\sqrt{n}}\cdot t_{(n-1;1-\alpha/2)} \ , \ \bar{X}+ \frac{S}{\sqrt{n}}\cdot t_{(n-1;1-\alpha/2)}\Big] $$

$\bar{X}$ = Durchschnitt = 85.74
S = 3.43
n = 29
$\alpha$ = 0.05, da weder besonders streng, noch besonders nachlässig

\[\begin{split} \Big[85.74- \frac{3.43}{\sqrt{29}}\cdot t_{(28;0.975)} \ , \ 85.74 + \frac{3.43}{\sqrt{29}}\cdot t_{(28;0.975)}\Big] \\ = [84.44,87.04] \notin 84.1 \end{split}\]

zu erwartender Wert für Industrienationen liegt mit 95%-iger Sicherheit über dem Wert, den Deutschland erreicht

Hypothesentest#