21.01.2022 langfristiges Wachstum#

Produktionswachstum: Wachstumsrate der Produktion der gesamten Wirtschaft

auch gemessen als:

  • Pro-Kopf-Wachstum

  • Wachstum der Arbeitsproduktivität (Output pro Arbeiter)

Geschichte des Wachstums#

  • Beginn um 1750 in England durch neue Maschinen = (technischer Wandel)

  • gesell. Wandel in städtische Industriegesellschaft

  • durch mehr Arbeitskräfte + Steigerung der Produktivität

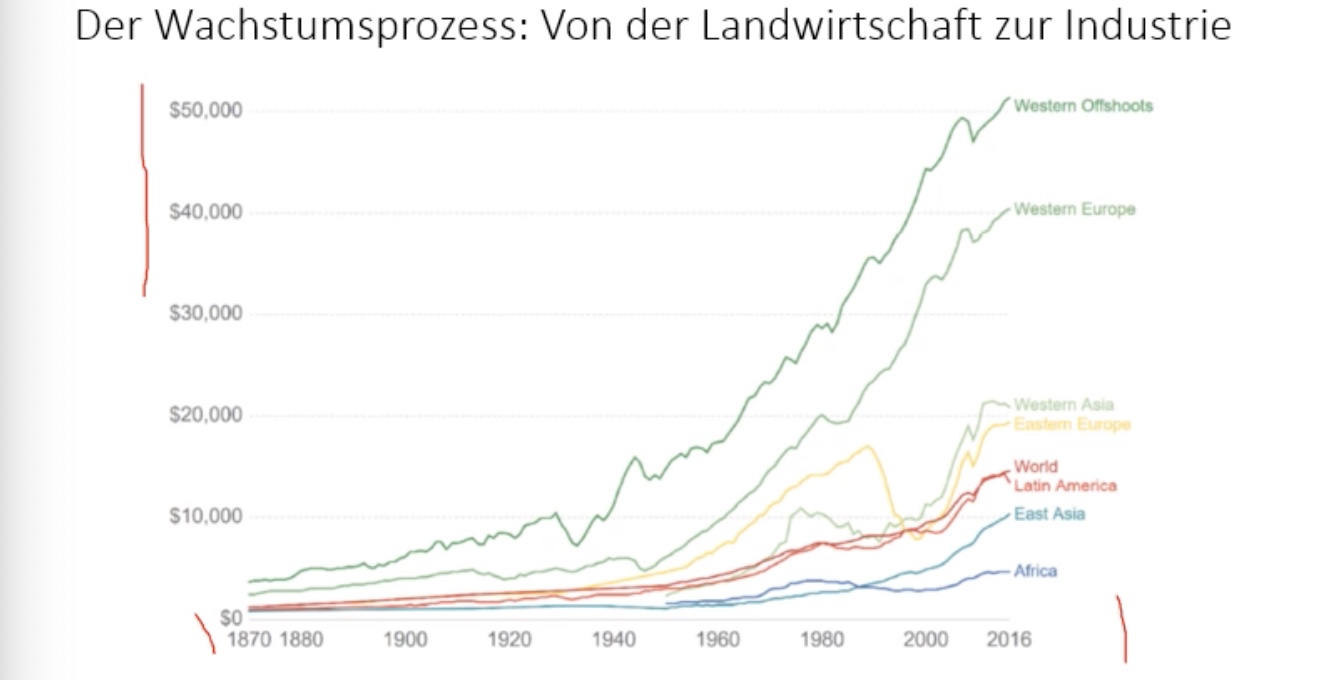
22-01-21_16-41

merke: The Great Divide = Auseinanderentwickeln der Staaten

verschiedene Ansätze zur Erklärung:

Aufholprozess#

  • entwickelnde Länder zu höheren aufholen

  • „Ausleihen“ der Technologien der entwickelten Länder

funktioniert nicht so ganz, nur unter bestimmten Voraussetzungen :

  • Kapital, Institutionen, Technologien

Quellen des Wachstums#

abhängig von aggregierter Produktionsfunktion

aggregierter Produktionsfunktion: mathematische Funktion, die Produktion abhängig macht von eingesetzer Arbeit und Kapital

Beispiel: \(Y = 3*K^{1/3} L^{2/3}\)

  • Produktivität = \(Y/L\)

  • Output pro Kapitaleinheit = \(Y / K\)

  • Kapitalrendite = \(\triangle Y / \triangle K\)

  • Kapitalintensität: Kapital pro Beschäftigtem

Zunahme der Arbeit#

  • steigende Erwerbsrate

  • Wachsende Bevölkerung

Bei gleichbleibendem Kapital = sinkende Produktivität

Zunahme des Sachkapitals#

  • steigende Ersparnisse

  • Ausländische Direktinvestitionen ADI

bei gleichbleibender Arbeit = sinkende Zinsen

Zunahme der Qualität der Arbeitskräfte#

  • historischer Anstieg des Bildungsniveaus

=> erhöhte Produktivität

Zunahme der Qualität des Kapitals#

  • neue Technologien / Innovationen

=> steigert Produktivität

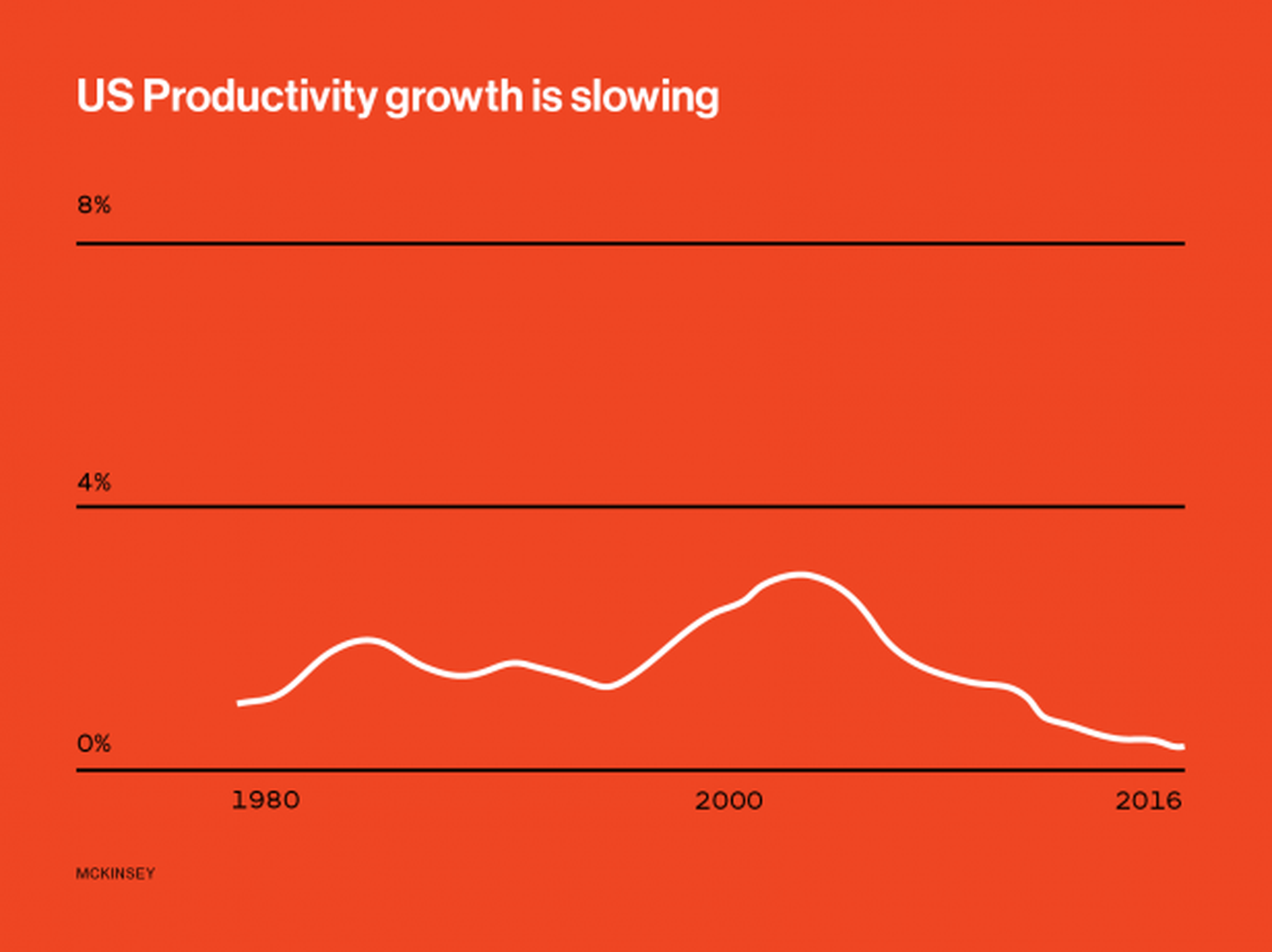
Produktivitätsparadox#

seit Jahren Grenzproduktivität steigt langsamer

  • Trotz Computer Age keine starken Produktivitätssteigerungen

22-01-21_17-30

Umwelt und Wachstum#

Gibt es einen Zusammenhang zwischen beiden?

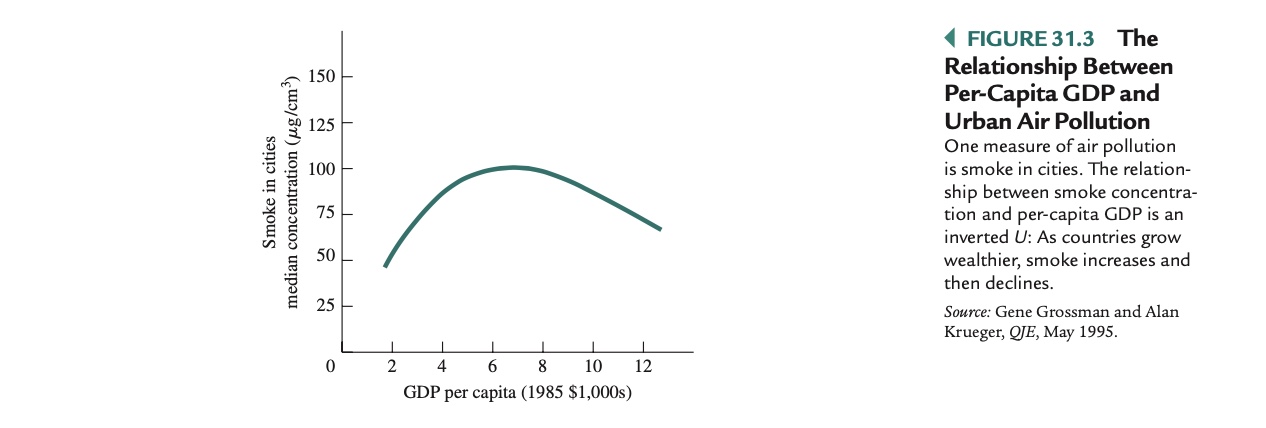
22-01-21_17-35

siehe dazu auch Club of Rome: Grenzen des Wachstums

Rechnungen#

Formeln#

  • Wachstumsrate je Zeiteinheit : \(p_t = \frac{x_t} {x_{t-1} } - 1\)

  • durchschnittliche Wachstumsrate pro Periode: \(\bar{p} = (\frac{x_n}{x_0})^\frac{1}{n} - 1\)

    • \(x_0\) Anfangswert

    • \(x_n\) Endwert

    • \(n\) = Anzahl Perioden

I. Beispielrechnungen hiermit22-01-28_14-02#

  • \(p_t\) 1980:2000 = (3806 / 1943) -1 => 0.959 = 95% Steigerung

  • \(\bar{p}\) 1980:2000 = (1943/950)^(1/20) -1 => 0.036 = 3,6 % pro Jahr Steigerung

II. Anwendung auf andere Einheiten#

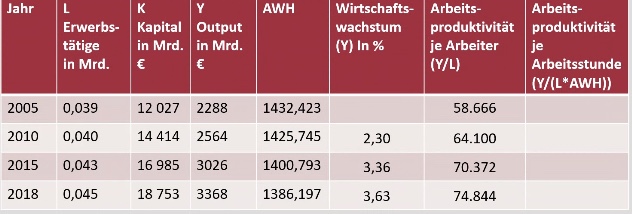
22-01-28_14-18

  • Wirtschaftswachstum 2005:2010 = (2564/2288)^(1/5) -1 => 0.023

  • Arbeitsproduktivität: \(\frac{Output}{Erwerbstätige * AWH}\)

    • AWH = Average working Hours per Year = Jahresarbeitszeit

    • 2005: 2288/(0.039*1432,423) => 0.041 = 4,1%

  • durchschnittliches Wachstum der Arbeitsproduktivität pro Arbeiter pro Jahr \(\bar{p} = (\frac{x_n}{x_0})^\frac{1}{n} - 1\)

    • 2005:2010: (64100/58666)^(1/5) -1 **=> 0.018 ** = 1,8%