05.06.2023 Tutorial 2#

Wages#

img

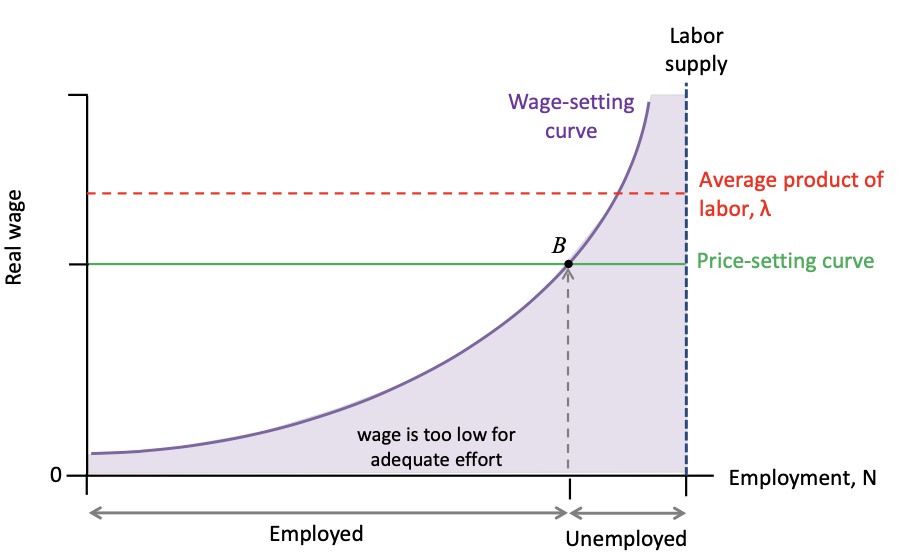
in Boom:

  • AD \(\uparrow\)

  • Firms hire more workers

  • Wage setting curve shifts \(\to\)

    • firms want more effort = more wages

    • price setting curve not (no increase in profits)

Smoothing#

Given

\[\begin{split} u = log(c_1)+ \frac{ 1 }{1+p}log(c_2) \\ c_1 + \frac{ c_1 }{1+r} = y_1 + \frac{ y_2 }{1+r} \\ \end{split}\]

Lambda for optimal

\[ L = \underbrace{log(c_1)+ \frac{ 1 }{1+p}log(c_2) }_{utility \ func} + \underbrace{\lambda \Big(y_1 + \frac{ y_2 }{1+r} - c_1 - \frac{ c_1 }{1+r}\Big)}_{budget \ constraint} \]

I) Diff wr.t \(c_1\)

\[\begin{split} \frac{ dL }{dc_1} = \frac{ 1 }{c_1} - \lambda = 0 \\ \to c_1 = \frac{ 1 }{\lambda} \end{split}\]

II) Diff w.r.t \(c_2\) $$ \frac{ dL }{dc_2} = \frac{ 1 }{1+p}\frac{ 1 }{c_2}

  • \lambda \big(\frac{ (1+r)*1-c_2 }{(1+r)^2}\big) \ \to c_2 = \frac{ (1+r) }{(1+p)} * \frac{ 1 }{\lambda} $$

III) Diff w.r.t lambda

\[ \frac{ dL }{d\lambda} = y_1+ y_2 - c_1 - \frac{ c_2 }{1+r} = 0 \]

Optiminzing c2#

a) Umstellen I nach Lambda

\[ \frac{ 1 }{\lambda} = \frac{ 1+p }{1+r}c_2 \]

b) Using \(c_1=...\) in III

\[\begin{split} \frac{ c_2 }{1+r} = y_1 + \frac{ y_2 }{1+r}- \frac{ 1 }{\lambda} \\ \end{split}\]

then: insert a in b

\[ \frac{ c_2 }{1+r} = y_1 + \frac{ y_2 }{1+r} - (\frac{ 1+p }{1+r})c_2 \]

optimal

\[ c_2^* = \frac{ 1 }{2+p} [y_1(1+r)+ y_2] \]

Optimize c1#

using II in III

\[\begin{split} y_1+ \frac{ y_2 }{1+r}-c_1- \frac{ 1 }{(1+p)} * \frac{ 1 }{\lambda} \\ c_1 = y_1+\frac{ y_2 }{1+r} - \frac{ 1 }{1+p} \frac{ 1 }{\lambda} \end{split}\]

input I (in umgestellter Form) in this

\[ c_1 = y_1+ \frac{ y_2 }{1+r}- (\frac{ 1 }{1+p})c_1 \]

Optimal

\[ c_1^* = \frac{ 1+p }{2+p} (y_1+\frac{ y_2 }{1+r}) \]

Banks#

Profit of Bank

Profit of a commercial Bank: $\( \Pi = \frac{rL^S - r^p (L^S-D-e)}{e} -\frac{1}{2} \frac{L^S}{e}^2 \)$

  • r = lending rate

  • \(r^p\) = policy rate

  • \(L^S\) = credit supply

  • \(D\) = customer deposits

  • \(e\) = equity

  • \(\frac{ L^s }{e}^2\) = risk of losing credit money

the Interest rate and Leves of Competition

  • perfect competition: \(r\)

  • imperfect comp: \(r\)

  • Monopoly: \(r \uparrow\)

optimal Credit supply: Diff w.r.t \(L^S\) $$ \frac{ d \Pi }{d L^S} = \frac{ r }{e} - \frac{ r^p }{e}

  • \frac{ 1 }{2} * 2\frac{ L^S }{e} \frac{ 1 }{e}=0 \

\implies L^S = e (r-r^p) $$ => bank will charge above policy rate