25.10.2022 Inflation#

Inflationserwartungen im Euroraum

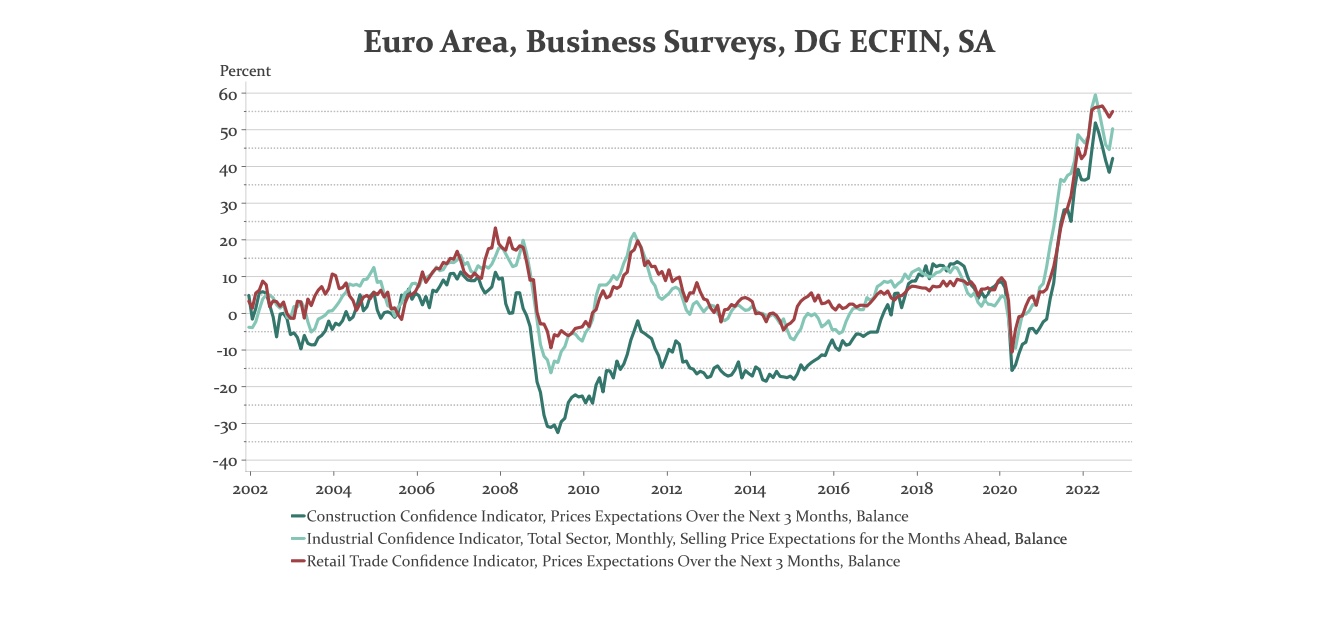
2022-10-25_16-27-19

Reaktion der EZB = Reduktion der Anleihekäufe auf 0

=> fallende Preise => steigende Zinsen

Zinsen und Renditen#

Ertrag = Kupon + Preisveränderung $(P_{t+1} - P_t)$

Rendite = Ertrag/Preis = $\frac{C+P_{t+1}-P_t}{P_t}$

Rendite = $i_c+g$:

Zinskupon $i_c = \frac{C}{P_t}$
Wertänderung $g = \frac{P_{t+1}-P_t}{P_t}$

Beispiel mit Laufzeit#

Anleihen mit Preis = 1000, kupon = 10%

Anleihe 1 = Laufzeit 1 Jahr
Anleihe 2 = Laufzeit 5 Jahre

Anleihe 1: was passiert bei (Effektiv)-Zinsänderung? $$ i=0.1: \; P = \frac{C+F}{(1+i)^1} =\frac{1000+100}{(1+0.1)^1}= 1000 \\ i=0.2: \; P = \frac{C+F}{(1+i)^1} =\frac{1000+100}{(1+0.2)^1}= \ 917 $$ **Anleihe 2:** $$ i=0.1: P = \frac{C}{(1+i)1} + \frac{C}{(1+i)^2} + ... + \frac{C+F}{(1+i)^n} \\ P = \frac{100}{(1+0.1)^1} + \frac{100}{(1+0.1)^2} + ... + \frac{1000+100}{(1+i)^n} = 1000 \\ i=0.2: P = \frac{100}{(1+0.2)^1} + \frac{100}{(1+0.2)^2} + ... + \frac{1000+100}{(1+2)^n} = 714 $$ => je länger die Laufzeit, desto stärker sinkt der Preis bei Zinssteigerung

= Abdiskontieren der zukünftigen Zahlungen $$ R_1 = \frac{C}{P_t}+ \frac{P_{t+1}-P_t}{P_t} = \frac{10}{1000}+ \frac{917-1000}{1000} = 1,7\% \\ R_2 = \frac{10}{1000}+ \frac{741-1000}{1000} = -15,9\% \\ $$ Längerfristige Papiere = höheres Risiko

Realzinsen#

Fischer Gleichung: Realzins = Nominalzins - Inflationserwartungen: $i_r = i-\pi^e$

Unterscheidung

Ex ante Realzins = berücksichtigt Erwartungen
Ex post = berücksichtigt realisierte Inflation

wichtiger Zins = realer Effektivzins

steigen Erwartungen, verlangen wir höheren effektiven Nominalzins
höherer Nominalzins => sinkender Papierpreis

höhere Inflationserwartung => Rückgang Anleihepreise

Übung#

1b)#

Effektivzins Berechnung: mit pq Formel

P = 900
F = 1000
$C = 100 \to i_c = 0.1$
t = 2

\[\begin{split} 900 = \frac{100}{(1+i)1}+ \frac{1100} {(1+i)^2} \\ 0 = \underbrace{\frac{100}{900}}_p(1+i) + \underbrace{\frac{1100}{900}}_q(1+i)^2 \\ (1+i)_{1/2} = \frac{p}{2} \pm \sqrt{\frac{p}{2}^2-q} \\ i_{1/2} = -1 + 0.0556 \pm 1.11069\\ \implies \bold{i_1 = 16.25\%} ;i_2 = -200\% \end{split}\]

1d)#

höhere Nominalverzinsung = höherer Preis => gleicher Effektivzins wegen Arbitrage

2) verschiedene Arten + Berechnung#

mit Werten aus der vorherigien Aufgabe: $P=900; C=100; t=2; F=1000$

Nullkuponanleihe: $$ C = 0 \to P = \frac{F}{(1+i)^t} \\ 900 = \frac{1000}{(1+i)^2} \\ (1+i)^2 - \underbrace{\frac{1000}{900}}_q = 0 \; \Big| \ p=0 \\ i_{1/2} = \pm\sqrt{\frac{1000}{900}} \\ \bold{i_1 = 0,9486}, i_2 = -0.9486 $$ bei einem einfachen Kredit ist das genau gleich! (nur anders gedacht)

Ratenkredit: $$ F = 0 \to 900 = \frac{100}{1+i} + \frac{100}{(1+i)^2} \\ (1+i)_{1/2} = \frac{100}{900} \pm \sqrt{\frac{100}{900}^2-\frac{100}{900}} \\ \bold{i_1 = -0.6065} $$ is nen schlechtes Geschäft alter

3) Verkauf einer Staatsanleihe#

Verkauf vor Ende der Restlaufzeit

$t_{Rest} = 1$
F = 5000
C = 8%
$i_1$ = 10% (ex ante)
$i_2$ = 15% (ex post)

Rendite = Ertrag + Wertänderung: $R = i+g = \frac{C}{P_t} + \frac{P_{t-1} - P_t}{P_t}$

Wir kaufen im Jahr vor Ablauf und verkaufen nächstes

berechnen Kurswert dieses Jahr und nächstes Jahr
berechne Ertrag bei Verkauf dieses Jahr
berechne Wertverädnerung, den Papier bis nächstes Jahr haben wird
dann Rendite

\[\begin{split} P_{t_1} = \frac{C+F}{1+0.1} = 4909.0909 \\ P_{t_2} = \frac{C+F}{1+0.15} = 4695.65 \\ i_c = \frac{i(=0.08) \cdot F(=5000)}{P_t(=4905.0909)} ?= 0.08148 \\ g = \frac{P_{t-1}-P_t}{P_t} = -0.0435 \\ R = i_c + g = 0.08148 - 0.0435 = 0.038 \end{split}\]

je näher Staatsanleihe an Ende, desto mehr nähert sich Kurswert dem Nennwert an

4) Inflationserwartung#

Fischer = Effektivzins - Erwartung

Erwartung 1 = 1%
Erwartung 2 = 3%
Effektivzins der Anlage = 5%

\[\begin{split} i_r = 5-1 = 4\% \\ i_r = 5-3 = 2 \% \end{split}\]

die Investoren wollen aber Realzins beibehalten
Die Nominalzinsen müssen steigen
ergo die Preise fallen