06.12.2021 Mehrdimensionale Merkmale#

meist ist bei statistischen Analysen mehr als ein Merkmal von Interesse => mehrdimensionale Merkmale

hier Fokus auf zwie Dimensionen

Zweidimensionale Merkmale#

zum Aussagetreffen immer gemeinsam erheben !

Darstellung mit Kontingenztafel:

  • zwei Merkmale X, Y

  • Ausprägungen:

    • \(a_1 ,..., a_k\) von X

    • \(b_1,...,b_m\) von Y

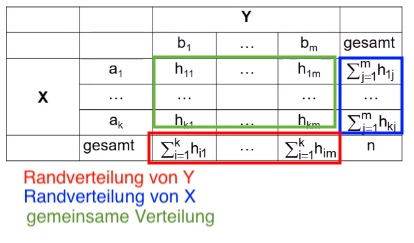
21-12-06_16-43

verkürzte Schreibweise: \(\sum_{j=1}^m h_{1j} = h_{1 \bullet}\) (Beispiel erste Zeile)

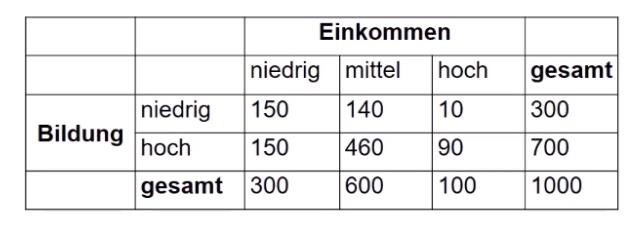
Beispiel Zusammenhang Einkommen <-> Bildung:

Absolute Verteilung

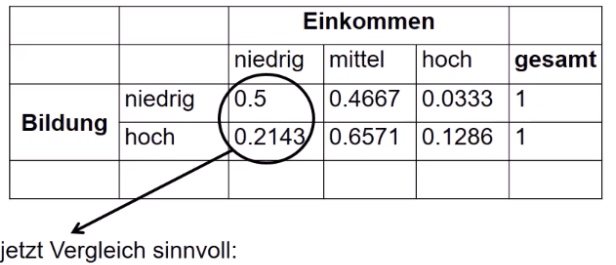
Bedingte Verteilung

21-12-06_16-30

Bedingte Verteilung: \(f_{\text{x}} = (a_i | b_j)\)

Beispiel:

  • bedingte Verteilung von X in Spalte 1, Zeile 1

  • \(f_{\text{x}} = (a_1 | b_1) = 0.5\)

  • 21-12-06_17-17

Vergleich der bedingten Verteilung ist subjektiv => Objektivierung mit Koeffizienten

Chi-Quadrat-Koeffizient#

Chi-Quadrat-Koeffizient: Koeffizient zur Einordnung des Zusammenhangs beider Variablen

\(\chi\) = Quadratische Abweichung der realen Werte von hypothetischen Werten

  • Werte: \(0 \le \chi \le \infty\)

  • hypothetische Tafel-Werte = Produkt der Randspalten / n : \(e_{ij} = h_{i\bullet} * h_{\bullet j} / n\)

  • für jede Tafelzelle: \(\frac{(real-erwartet)^2}{erwartet}\)

  • Aufaddieren der Ergebnisse der Zellen

Notation: 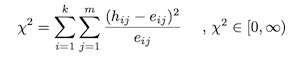21-12-06_17-46

zum Normieren von Chi => Kontingenzkoeffizient

  • Kontingenzkoeffizient: \(K = \sqrt{\frac{\chi^2}{n+\chi^2}}\)

  • Normierter: \(K^* = \frac{K}{\sqrt{\frac{M-1}{M}}}\) mit M = min{k,m} (kleinere Zahl von Spalte/Zeilen)

Interpretation \(K^*\):

  • \(0 \le K^* \le 0.2 \to\) Kein Zusammenhang

  • \(0.2 \le K^* \le 0.5 \to\) schwacher Z.

  • \(0.5 \le K^* \le 0.8 \to\) deutlich

  • \(0.8 \le K^* \le 1 \to\) Stark