05.05.2022 Arbeitsmarkt

Wiederholung: mikroökonomisches Modell

graph LR subgraph exogene Var. Demand & Supply end Demand & Supply --> M[[Modell]] M --> Preis & Menge subgraph endogene Var. Preis & Menge end

never start reasoning from Price / Quantity Change!

Inputfaktoren der Produktion

Frage: woher kommen die Produktionsfaktoren der Unternehmen?

Produktionsfaktoren:

• Arbeit L für Lohn w

• Kapital K für Zinsrate i

beide kommen von Haushalten als Anbieter

Darstellung: Arbeitsmarkt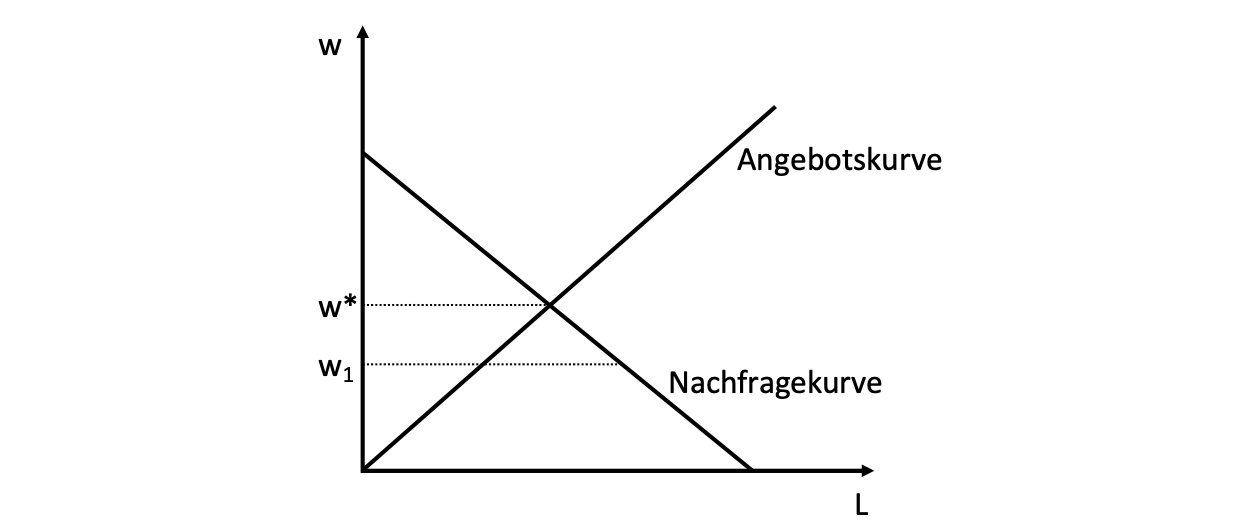

Arbeitsnachfrage

Produktionsfunktion eines Unternehmens für den Faktor Arbeit bei konstanten Kapital: \(x(L, \bar{K})\)

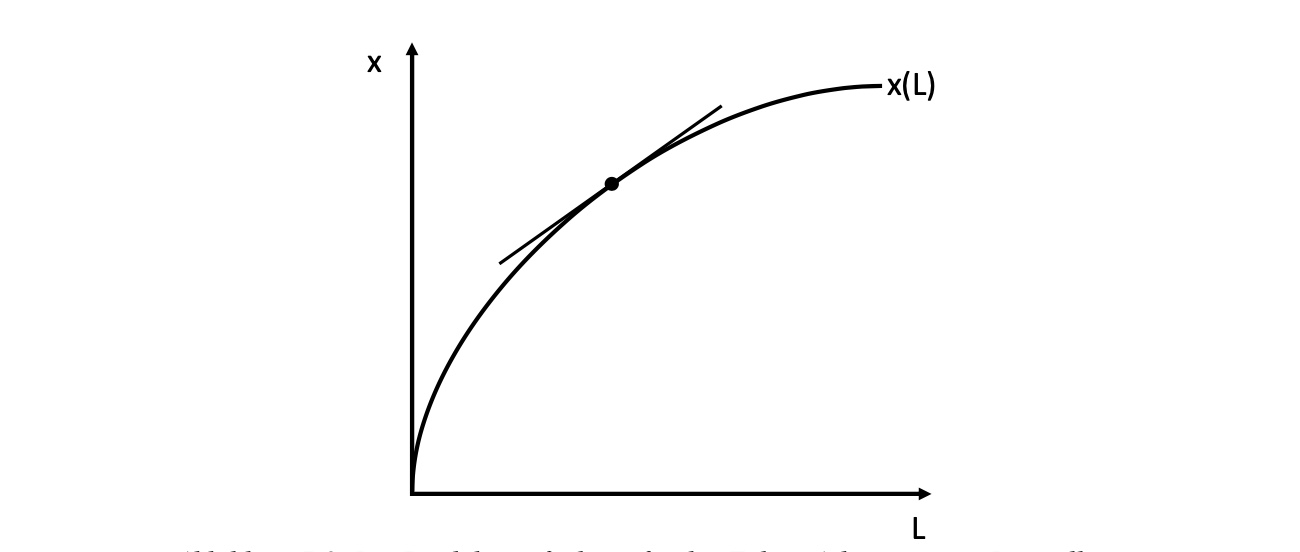
• Grenzproduktivität: \(\frac{\partial X}{\partial L} > 0\) , oder eine Einheit mehr Arbeit => wieviel mehr Güter?

Gewinnfunktion eines profitorientierten Unternehmens: $\( \begin{aligned} G &= p*x(L,K) - C(L,K) \\ &= p*x(L,K) - w*L-i*K \end{aligned} \)\( rationaler Arbeitseinsatz = erste Ableitung \)$ \frac{\partial G}{\partial L} = p*\frac{\partial x(L,K)}{\partial L}

• \frac{\partial C(L,K)}{\partial L} \ \to p * \frac{\partial x(L,K)}{\partial L} - w = 0 \ \implies \bold{w = p * \frac{\partial x(L,K)}{\partial L}} = WGP_A $$

Wertgrenzprodukt der Arbeit WGP: Beitrag des letzten eingestellten Mitarbeiters zum Umsatz = Grenzvorteil

dazu sind Grenzkosten die Lohnkosten

Schocks der Nachfrage

• Marktpreis p des angebotenen Gutes steigt \(\implies WGP_A \uparrow \implies N \uparrow\)

• Technologie Veränderung \(\implies \frac{\partial x}{\partial L} \implies N \uparrow\)

• steigender Kapitaleinsatz -> zwei Optionen:

  • K und L sind komplementär => Grenzproduktivität \(\frac{\partial x}{\partial L} \uparrow \implies N \uparrow\)

  • K und L sind substitutiv => Grenzproduktivität \(\frac{\partial x}{\partial L} \downarrow \implies N \downarrow\)

Arbeitsangebot

Opportunitätskosten der Arbeit für Haushalte = verlorene Freizeit

• Arbeitsangebot = Haushalts-TradeOff-Entscheidung zwischen Arbeit und Freizeit

• Angebotskurve = Veränderung der Arbeit bezüglich Lohnsatz w

also: Lohn = Grenzkosten der Freizeit

Einkommen \(I = w * t_A\) (Lohn * Arbeitszeit)

Effekt einer Lohnerhöhung auf eine Haushaltsentscheidung: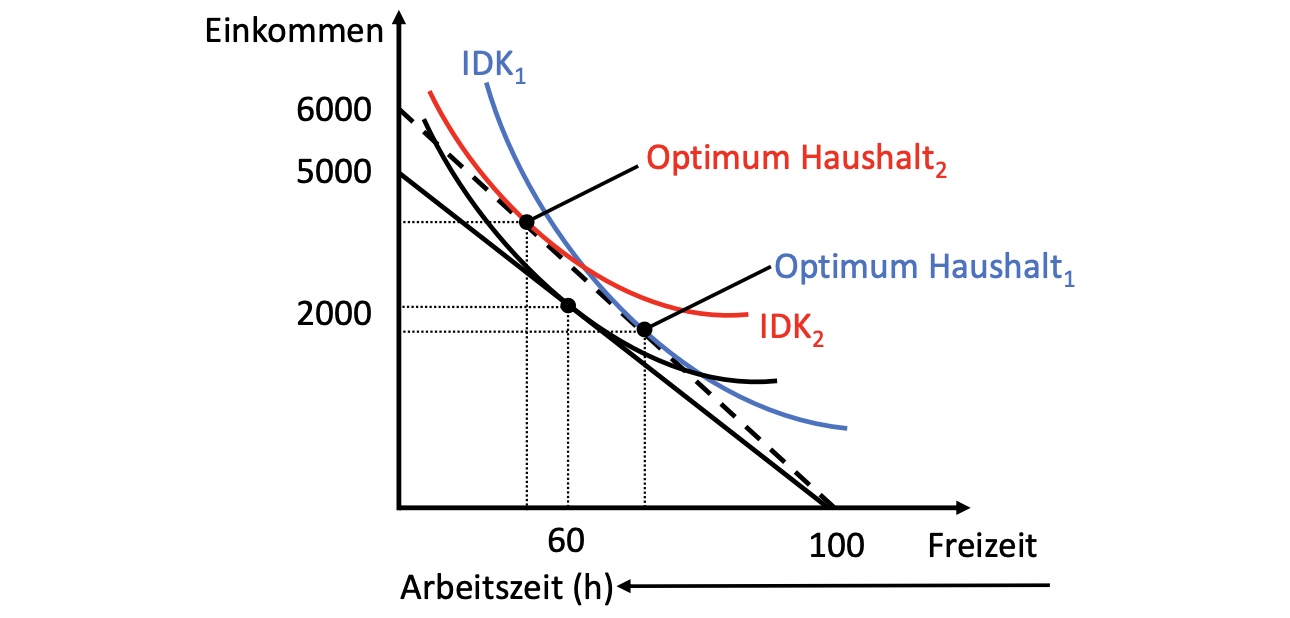

persönliche Präferenzen abhängig von Einkommenseffekt (EE) und Substiutionseffekt (SE)!

• Haushalt 1 = starke Freizeitpräferenz

  • Lohnerhöhung: EE > SE

• Haushalt 2 = niedrige Freizeitpräferenz

  • Lohnerhöhung: SE > EE

---

Lösung des Freizeitproblems für Unternehmen: Überstundenlohn

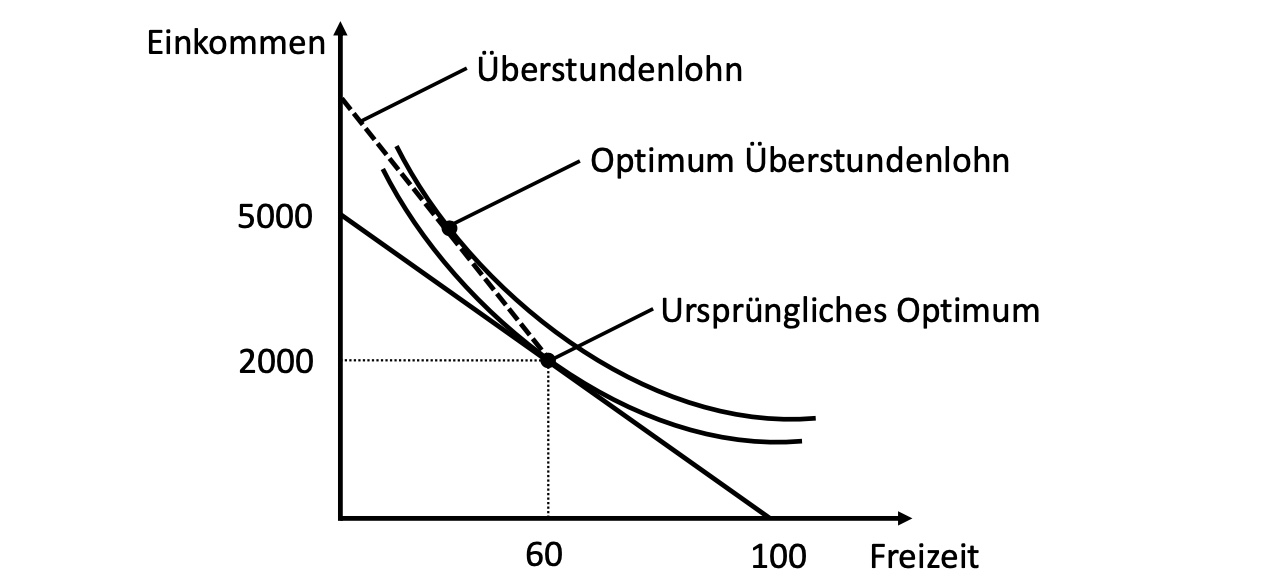
• Kann nur in Richtung mehr Arbeitszeit führen

Zeitallokation

Frage: wieviel Lernen für die nächste Klausur?

• Klausurergebnis S zwischen 0 und 100 Punkten

• Arbeitseinsatz \(t_w\)

• Student hat Interesse an Freizeit \(t_F\) und S

  • Nutzenfunktion \(U(t_F,S)\) mit \(\frac{\partial U}{\partial t_F}> 0\) und \(\frac{\partial U}{\partial S}> 0\)

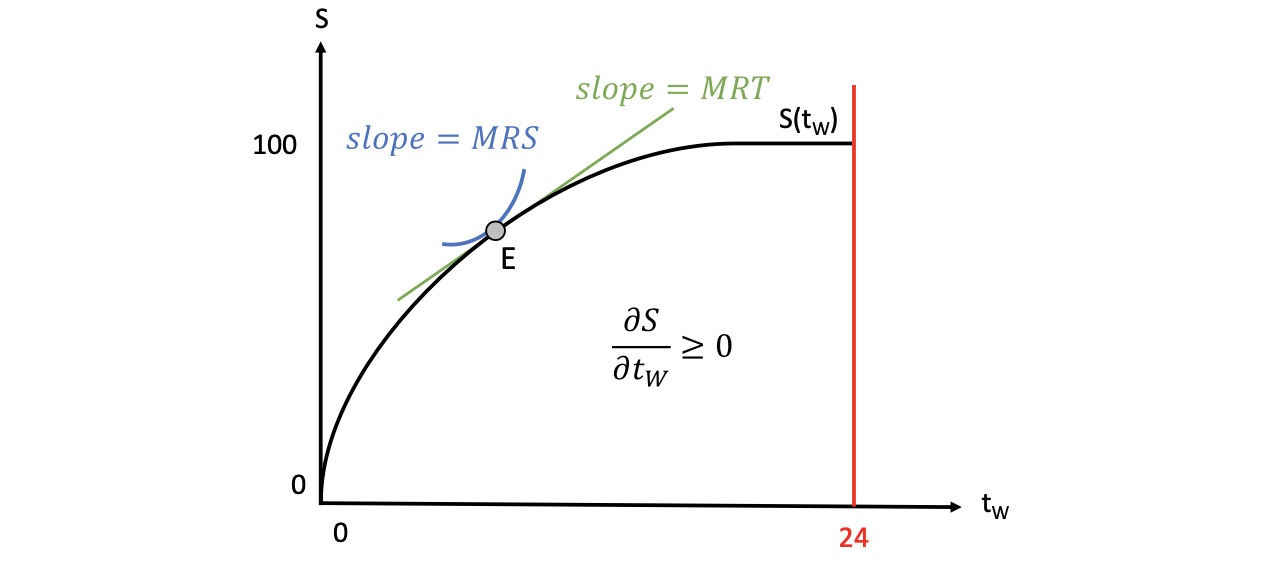
• Steigung der Gerade: \(\frac{\partial S(t_w)}{\partial t_w} \ge 0\)

• Zeitrestriktion \(T = t_F + t_W\)

Lagrange-Funktion aufstellen und ableiten: $\( L = U \big(t_F, S(t_W) \big) + \lambda * [T- t_F - t_W] \\ \begin{aligned} \to \frac{\partial L}{\partial t_F} &= \frac{\partial U}{\partial t_F} - \lambda = 0 \\ \to \frac{\partial L}{\partial t_W} &= \frac{\partial U}{\partial S} \frac{\partial S}{\partial t_W} - \lambda = 0 \end{aligned} \)\( Gleichsetzen der beiden Lambdas: \)$ \frac{\partial U}{\partial S} \frac{\partial S}{\partial t_W} = \frac{\partial U}{\partial t_F} = \lambda \

MRS\bigg{ \frac{\frac{\partial U}{\partial t_F}}{\frac{\partial U}{\partial S}} = \frac{\partial S}{\partial t_W} \bigg} MRT $\( \)\lambda$ = Grenznutzen der Zeit

• Änderung der Nutzenfunktion, wenn Restriktion T um eins gelockert wird

• Ist ausgeglichen zwischen beiden Zeitnutzungen (im Optimum)

Arbeitslosigkeit

woran kann es liegen?

1. Erklärung: Der Mindestlohn/Tariflöhne sind schuld (empirisch nicht nachgewiesen!)

2. Erklärung: Effizienzlohntheorie

Effizienzlohntheorie

Ausgangsituation:

• Arbeitgeber AG können Mitarbeiterleistung nicht (komplett) kontrollieren

• zahlen deswegen höheren Lohn (als Vergleichslohn) für Effizienzanreiz

Folgen:

• alle AG versuchen Löhne zu erhöhen

• künstliche Erhöhung des Preises der Arbeit => sinkender Nachfrage

• AN können sich nicht in den Markt hineinpreisen, da Unternehmen ja nur höhere Löhne zahlen wollen

• Arbeitslosigkeit als Effekt

Übung

Aufgabe 1: Arbeitsnachfrage

Produktionsfunktion \(L^{1/2}\)

Gewinnoptimum: \(G(L) = E(L) - C(L) = p*x(L) - w*L\)

ableiten nach der Arbeit und 0 setzen $\( \frac{\partial G}{\partial L} = p \frac{\partial x}{\partial L} - w = 0 \\ \to w = p * \frac{\partial x}{\partial L} \\ \to \frac{\partial x}{\partial L} = \frac{w}{p} \text{ Steigung der Produktionsfunktion} \)\( für p = 4 \)\( w = p * \frac{\partial x}{\partial L} = 4 \frac{1}{2}*L^{-1/2} = \frac{2}{L^{1/2}} \)$

L	0	1	4	9
w	0	2	1	2/3

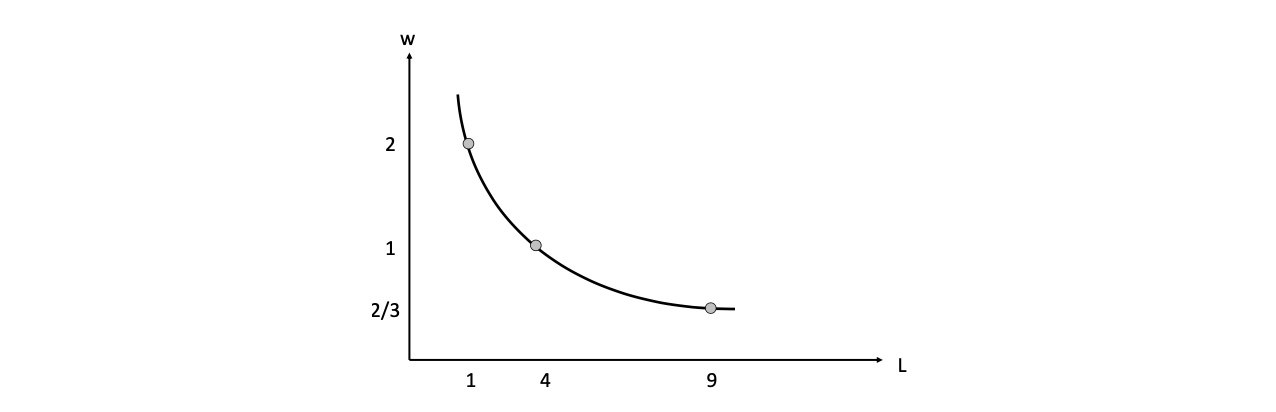
Nachfrage nach Arbeit bei w=1 und p=4 $\( 1 = 2*L^{-1/2} \to& L = 4 \\ x = L^{1/2} = 4^{1/2} \to& x = 2 \\ G = p*x - w*L = 4*2 - 4 \to& G = 4 \)$

Aufgabe 2: Preisänderung auf Absatzmarkt

Nachfrageerhöhung auf p=6, w=1 bleibt $\( w = p * \frac{\partial x}{\partial L} \to 1= 6 * \frac{1}{2} * L^{-1/2}\\ \to 1/3^{-2} \to & L = 9 \\ x = 9^{1/2} \to & x= 3 \\ G = 6*3 - 9 \to& G = 9 \)$

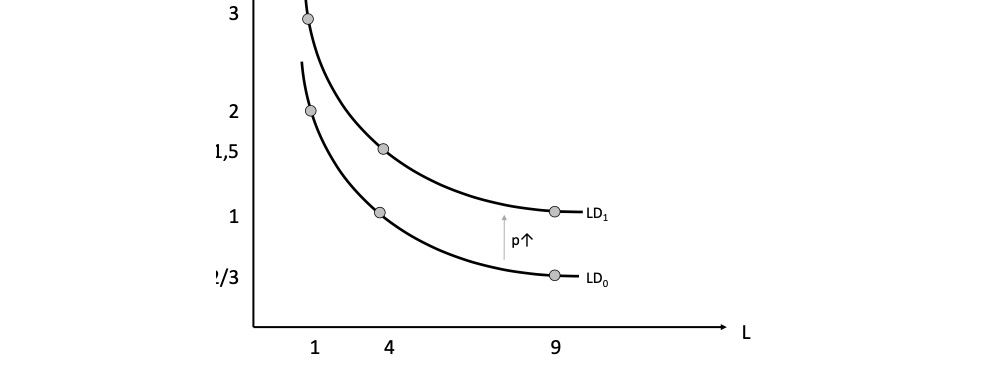
Aufgabe 3: Produktivitätssteigerung

gegebenes w=1 und p=4, neue Produktionsfunktion

neues Optimum: $\( \implies x = L^{3/4} \\ w = p * \frac{\partial x}{\partial L} \to 1 = 4*\frac{3}{4}*L^{-1/4} \\ L = 1/3^{-4}\to & L = 81 \\ x = L^{3/4} \to 81^{3/4}\to & x= 27 \\ G = 4*27 - 1*81 \to & G=  27 \)\( um altes Output x=2 zu erreichen \)\( 2 = L^{3/4} \to 2^{4/3} = 8/3 \)\( neue Nachfragekurve: \)\( w = p * \frac{\partial x}{\partial L} = \frac{3}{L^{1/4}} \)$ neue Punkte einsetzen und zeichnen