24.11.2022 Arbeitsmärkte#

Erwerbstätigkeit#

  Erwerbstätige 
+ Erwerbslose
----------------
= Erwerbspersonen
+ Nicht-Erwerbspersonen (Kinder, Rentner,...)
----------------
= Bevölkerung

img

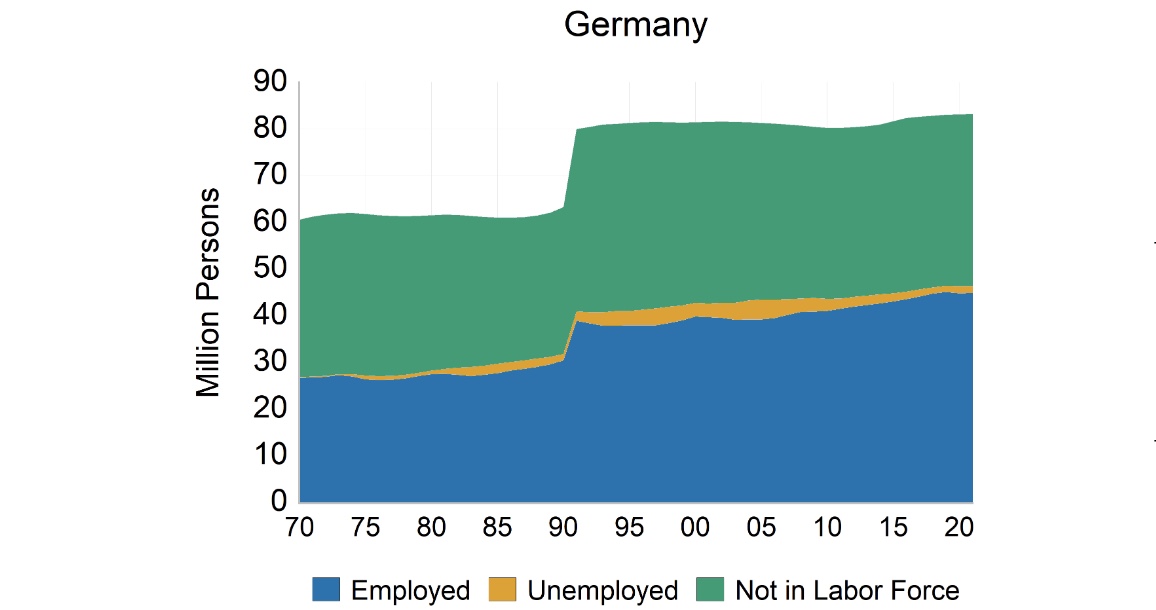
Aus Makro-Datenbank der EU: AMECO

Definitionen#

  • Arbeitslosenquote (ALQ): Verhältnis Arbeitslose | Erwerbspersonen

  • Bevölkerung im erwerbsfähigen Alter: zw. 15 und 64

  • Partizipationsquote: Verhältnis Erwerbspersonen | Bevölkerung erwerbsfähiges Alter

  • Weder arbeit suchen noch finden = nicht arbeitslos

Wege in dem Arbeitsmarkt 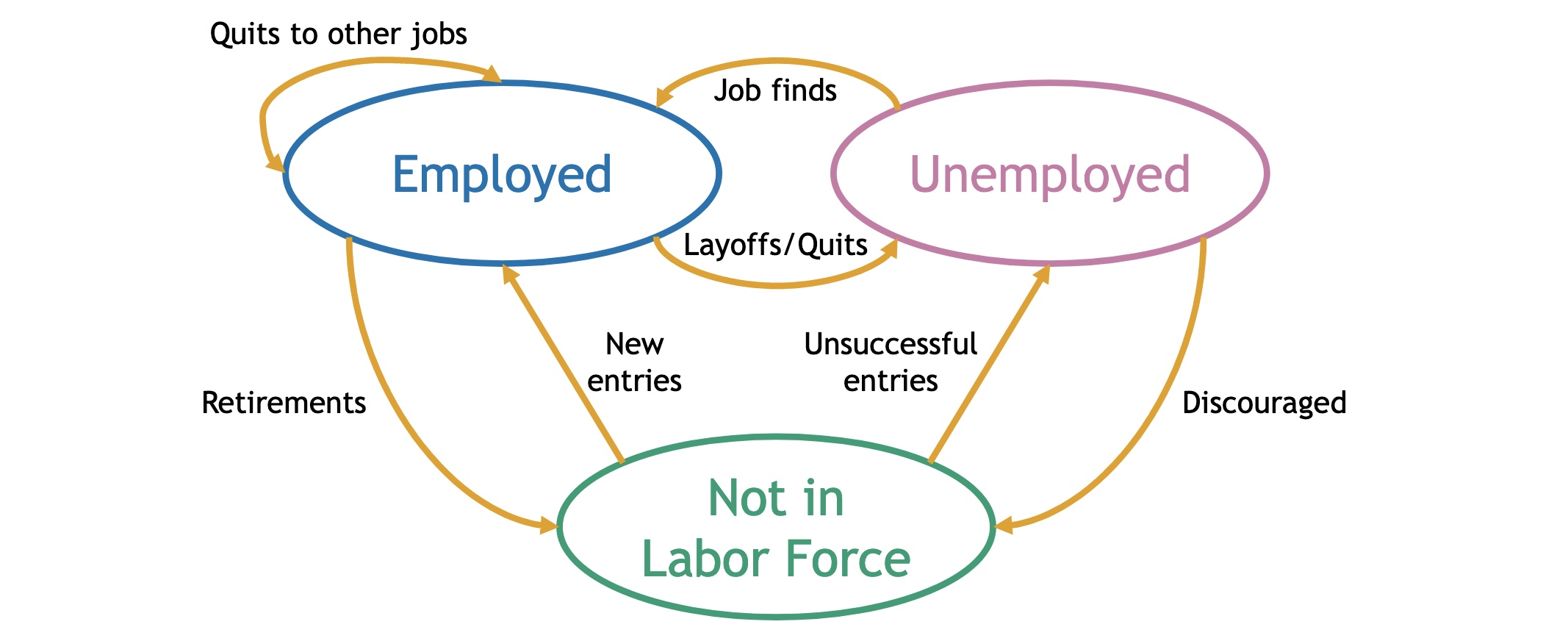img

Lohnbildung#

in Deutschland: Kollektivlohn

  • ausgehandelt zwischen Arbeitnehmern und Arbeitgebern

    • DGB = Gewerkschaftsbund mit ~6 Mio Mitlgiedern

    • BDA = Arbeitgeberbund mit 1 Mio. Unternehmen und rund ~20 Mio Beschäftigte

img

Kräfte, die beeinflussen:

  • Reservationlohn = Lohn, bei dem AN indifferent zu Arbeitslosigkeit

  • Lage am Arbeitsmarkt (ALQ)

Vergleich der Gewerkschaftsbewegungen

img

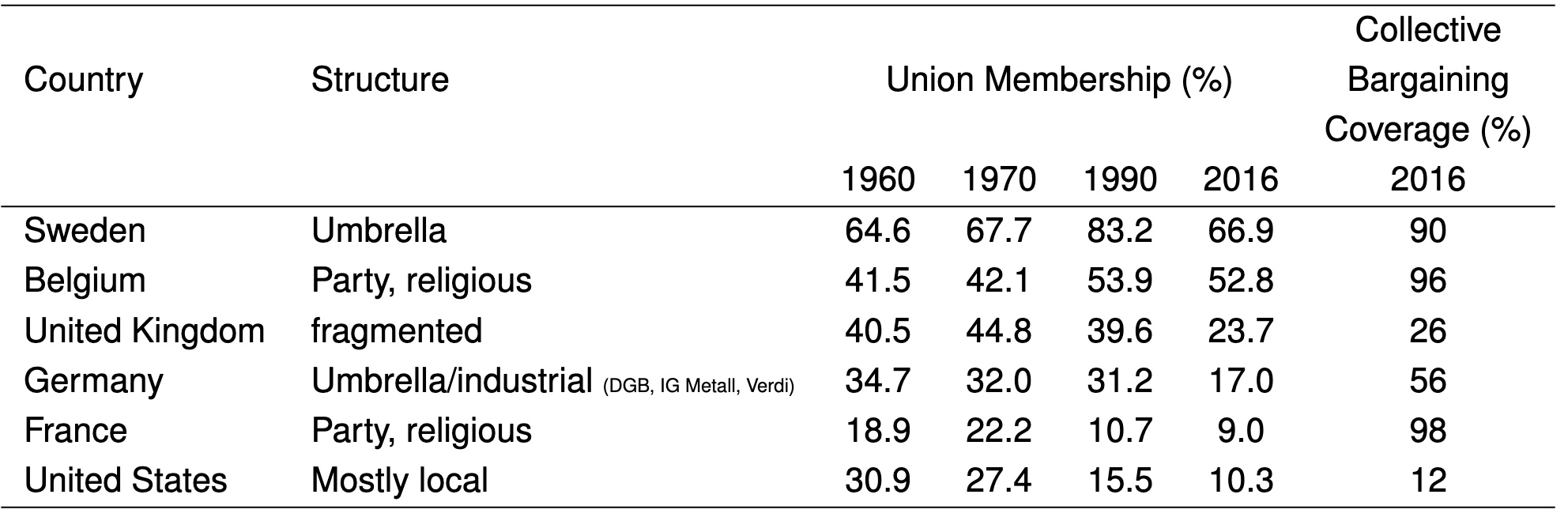
=> Mitgliedschaft sagt noch ncihts über die Stärke (Bargaining Power) aus (siehe Frankreich)

Verhandlungsmacht hängt ab von:

  • alternative Arbeiten

  • Kosten für Arbeiterersetzung

Effizienzlohntheorie#

annahme, dass Lohn mit Motivation der Arbeiter zusammenhängt

  • somit macht Lohn über Reservationslohn Sinn

  • bspw. High-Tech Unternehmen, wo viel von Mitarbeiten abhängt

Gesamtwirtschaftlcihe Nominallohn $\( W = P^e\cdot f(\overset{-}{u}, \overset{\pm}{z}) \)$ Bestandteile:

  • \(P^e\) = erwartetes Preisniveau

    • wichtig ist Reallohn, nicht Nominallohn

    • AN wollen wissen was sie sich leisten können

    • AG wollen Verhältnis Verkaufspreis / Kosten

  • \(u\) = ALQ

    • hohe ALQ = niedrige Verhandlungsmacht

  • \(z\) = restliche Faktoren (insb. institutionell)

    • kann positiv oder negativ sein

Preisbildung#

Annahme: monopolistische Konkurrenz

  • gewisser Spielraum für Preise über Grenzkosten

  • mit Gewinnmarge \(\mu\) abhängig von Marktmacht

\[ P= (1+ \mu) \cdot MC \]

Annahme: in kurtzer Frist Produktionssteigerung nur mit mehr Arbeit! (K=konst.)

Marginalkosten dann: $\( MC = \frac{W}{\underbrace{MPL}_{Grenzprod.}} \)$

Strukturelle Arbeitslosigkeit#

daraus resultiert: (bei langfristig \(P^e = P\))

Lohnsetzungsgleichung: $\( W = P \cdot f(u,z) \ | :P \newline \underbrace{\frac{W}{P}}_{\text{Reallohn}} = f(u,z) \)$ Graphisch:

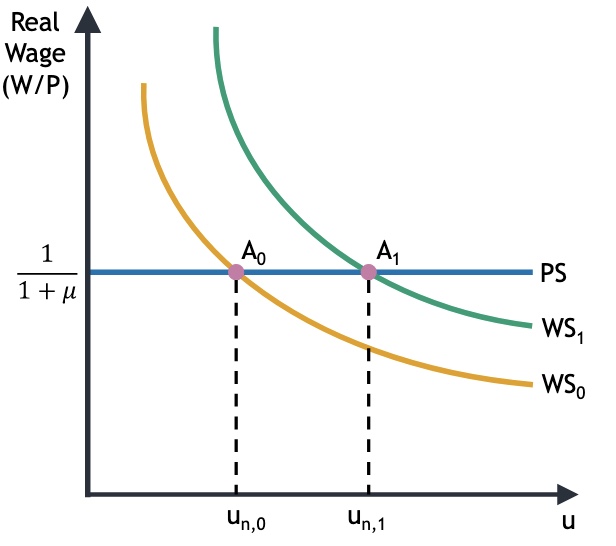
  • Wage Setting (WS) = negativ wegen u

  • Price Setting (PS) = gerade, aber abhängig von Marktmacht \(\mu\)

img

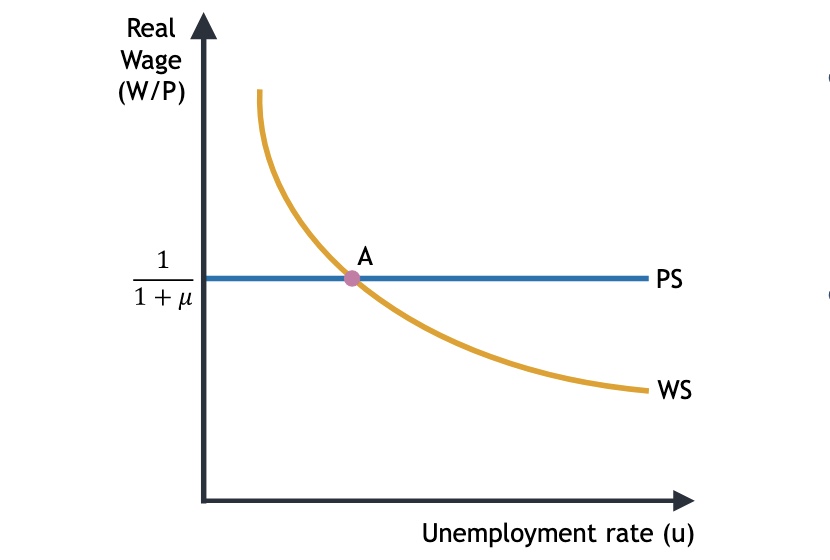
Schnittpunkt = strukturelle Arbeitslosigkeit \(u_n\) (die nicht konjunkturell)

  • Abhängig von z = Arbeitslosenunterstützung

  • und \(\mu\) = Marktmacht

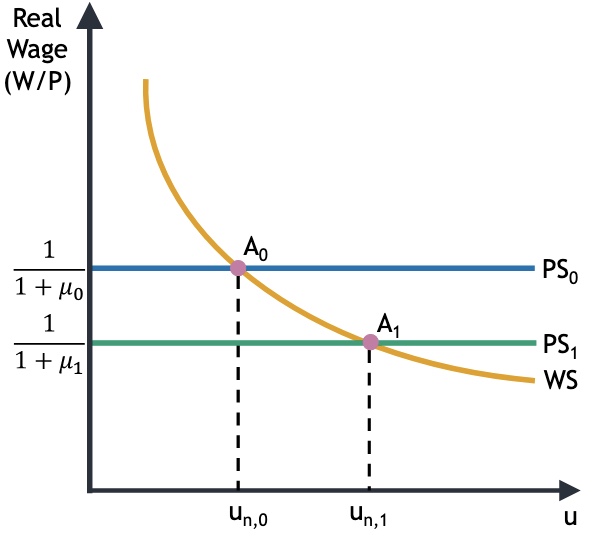
mögliche Situationen

mehr Arbeitslosenuntersützung z

höhere Marktmacht \(\mu\)

img

img

Produktionspotenzial dann: $\( Y_n = F(K,A \ (1-u_n)L) \)$ => Je niedriger strukturelle AL, desto höher Produktionspotenzial

Einkommensverteilung#

Reallohn bei Cobb-Douglas Prod.Funktion $\( \frac{W}{P} = \frac{1-\alpha}{1+\mu}\frac{Y}{N} \)$ Y/N = Arbeitsproduktivität, Reallohn entwickelt sich ungefähr im Gleichklang

img

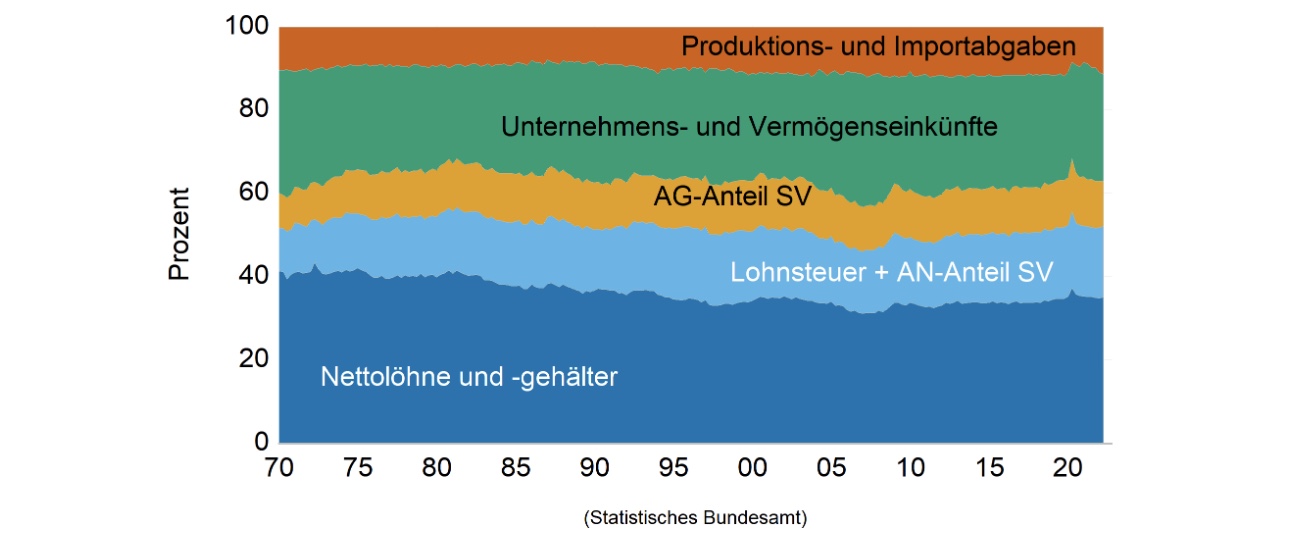
Lohnquote = Anteil Arbeitseinkommen an Gesamteinkommen ( WN/PY )

  • je größer Marktmacht, desto weniger Lohnquote!

Übung#

Gleichgewicht auf dem Arbeitsmarkt: Herleitung

  • Preissetzung: \(P = (1+\mu) \cdot MC\)

    • mit \(MC=\frac{W}{MPL} \to MC = W\) (vereinfachte Annahme)

    • Also: \(P= (1+\mu)W\)

  • Lohnsetzung: \(W= P\cdot f(u,z)\)

umstellen nach Reallohn: \(\frac{W}{P}\)

  • Preissetzung: \(\frac{W}{P} = \frac{1}{(1+\mu)}\)

  • Lohnsetzung: \(\frac{W}{P} = f(u,z)\)

Gleichsetzen: \(\frac{1}{(1+\mu)} = f(u,z)\)

Strukturelle Arbeitslosigkeit (im Gleichgewicht) $\( f(u_n,z) = \frac{MPL}{(1+\mu)} \)$ Gegeben:

  • \(f = z(1-u)^2\)

  • MPL = A = 1

  • z = 1

  • \(\mu = 0.25\)

\[ (1-u_n)^2 = \frac{1}{1+0.25} \newline 1-u_n = \sqrt{0.8} \to u_n = 1-\sqrt{0.8} = 0.1055 \]

die strukturelle Arbeitslosenquote beträgt 10,55 %

Reallohn = \(\frac{1}{1+\mu} = 0.8\)