31.05.2022 Öffentliche Güter

Kategorisierung von Gütern:

• Rivalität: Güter können nur einmal genutzt werden

  • Frage der situativen Knappheit

• Auschließbarkeit: andere können von Konsum ausgeschlossen werden

  • Frage der juristischen Definition

Güter	Rivalität	Nicht-Rivalität
Auschließbarkeit	private G.	Clubgüter
Nicht-Auschließbarkeit	Allmende G.	öffentliche G.

Allmende auch Common-Pool-Resources CPR

Güter sind nicht fest einer Kategorie zugeordnet!

• bspw. Straßen sind abhängig von Verkehrsmenge und Maut anders

  • Clubgut: Mautstraße

  • Privates G.: Mautstraße mit viel Verkehr

  • öffentliches Gut: deutscher Feldweg in Buxtehude Nord

  • CPR / Allmende: deutsche volle Autobahnen

Trittbrettfahren

Problem: für öffentliche/CPR Güter will niemand zahlen, da man nicht ausgeschlossen werden kann => Trittbrettfahrerproblem = Bereitstellungsproblem

• Staat bietet Güter als Clubgüter an (für Einwohner gegen Steuern)

• durch Verknappung werden öffentliche zu CPR

  • Lösung mithilfe Umwandlung in private Güter (Treibhauszertifikate)

Bereitstellung Ö.G.

wie stellt man öffentliche Güter effizient bereit?

bei privaten Gütern die marginale Zahlungsbereitschaft aggregierten, ebenso bei öffentlichen Gütern

Modellierung:

• Öffentliches Gut = Public Good = PG

  • Kosten \(C(PG)\)

  • Individueller Nutzen = \(U_i(PG)\)

• Gesamtgesellschaftliche Zahlungsbereitschaft \(p_G\)

  • Summe der individuellen Zahlungsbereitschaften \(p_i = \frac{\frac{\partial U_i}{\partial PG}}{\lambda_i}\)

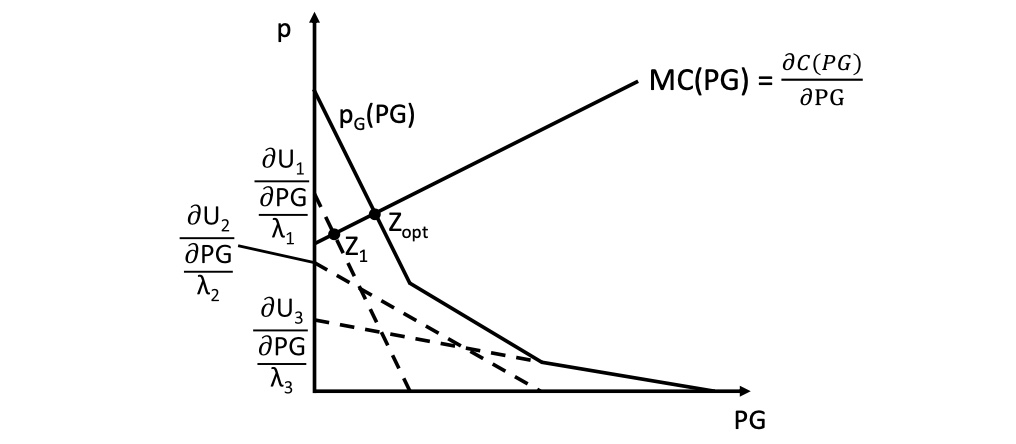
nur Haushalt 1 wäre hier bereit, das Gut alleine herzustellen und würde von den anderen beiden ausgebeutet => Staat übernimmt Aufgaben

Besteuerung schafft die Basis für die Bereitstellung von Ö.G.

Allmende Güter

Beispiel: Aplenwiese, die von allen gemeinsam genutzt werden kann

• x Kühe mit Produktionsfunktion f(x)

• Milchpreis p

• Kosten einer Kuh c

• gemeinsamer Tank mit geteiltem Ertrag über Durchschnitt für alle

Gewinnfuntkion: \(G(x) = p \cdot f(x) - c \cdot x\)

normales Gewinnmaximum: \(p \cdot f'(x^{opt}) = c\)

bei Allmende: \(p \cdot f(x) \cdot \frac{x_i}{X}-x_i = c\)

• langfristig ist Gewinn 0, und das Allmende Gut wertlos

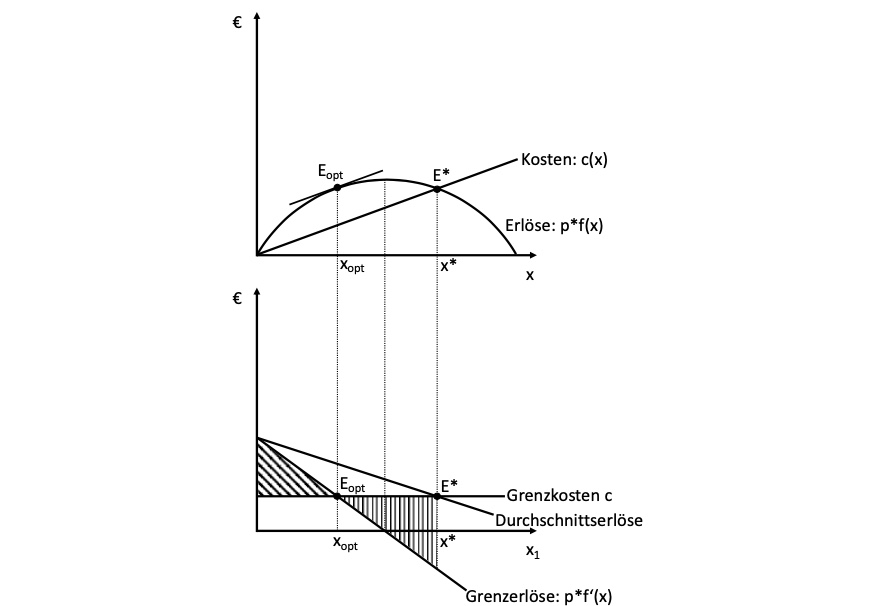
=> Tragik der Allmende

Möglichkeiten, dieses Problem zu verhindern:

• Weidegebühr pro Kuh

• Parzellierung der Wiese

• Mengenrestriktion der Kühe

Spieltheorie

Analyse der Strategien

• einer Gruppe von Akteuren (meist 2)

• bei begrenzten Handlungsalternativen (meist 2)

Darstellung mit Pay-Off-Matrix

Beispiel Kartell

• Kartellmitglieder sind alle am besten gestellt, wenn gemeinsamer Preis vereinbart wird (Kooperation)

• für individuelle Mtglieder liegt dann Anreiz vor, das zu unterlaufen (Defektion)

hier: 2 Mitglieder.

• Kooperation: jeder verkauft 3 Einheiten (3,3)

• Defektion für ein Mitglied: es kann jetzt 4 Einheiten verkaufen, anderer nur noch 1 (4,1)

• beide weichen ab => beide verkaufen nur noch 2 (2,2)

  • = Nash-Gleichgewicht

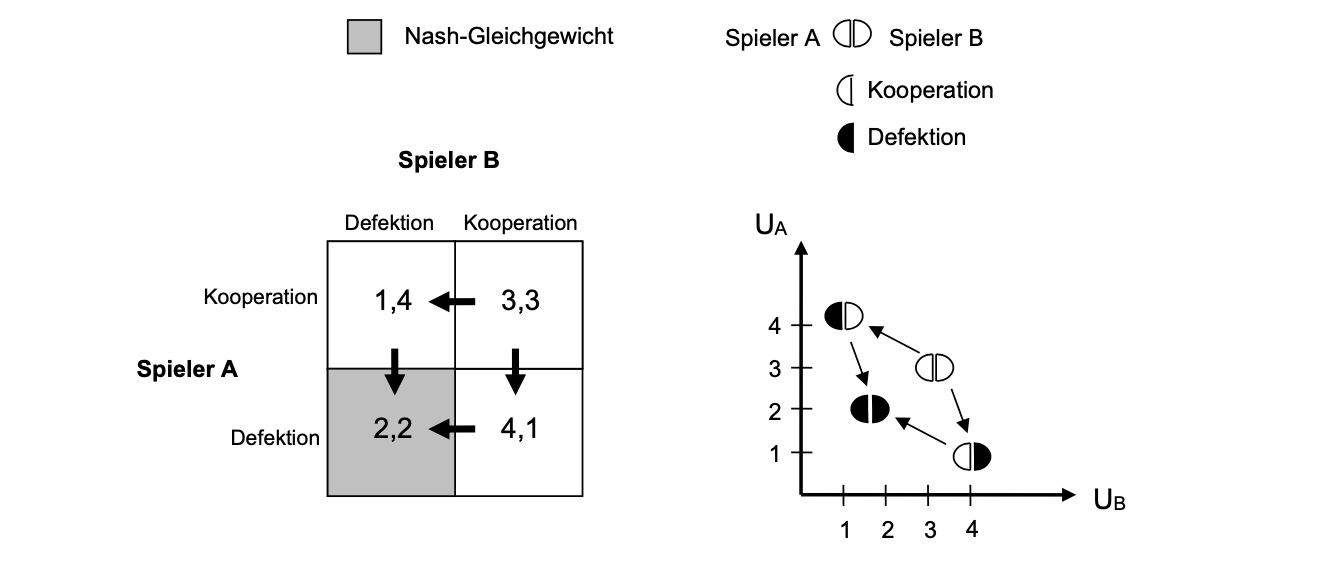
profitable Kooperation kann irrational sein!

(2,2) ist pareto-inferior gegenüber (3,3)

Übung

Zahlungsbereitschaft Öffentliche Güter

zwei Nachfrager A und B

• \(D_A: p = -x+6\)

• \(D_B: p= -0.5x+3\)

individuelle Zahlungsbereitschaften für ein Gut:

• \(p_A = -1+6 = 5\)

• \(p_B = -0.5*1+3 = 3.5\)

gemeinsame zahlungsbereitschaft:

• vertikale Addition der Bereitschaften

• \(D_A+D_B = -x+6 - 0.5x+3 = -1.5x+9\)

• für ein Gut: \(-1.5+9 = 7.5\)

warum vertikale Addition?! Fragen!

Antwort:

• horizontal Aggregieren = Summieren der Menge bei privaten Gütern

• vertikal Aggregieren = Summieren der Zahlungsbereichtschaften für öffentliche Güter, da öffentliche Güter nicht teilbar sind!

Bereitstellung des öffentlichen Gutes

Beispiel: MC = 6

individuelle Bereitstellung? nein, da unter Zahlungsbereitschaft

gemeinsame Bereitstellung? Ja, da MC über Zahlungsbereitschaft

bereitgestellte Menge: MC = D $\( -1.5x+9 = 6 \\ \to x^* = 2 \)$

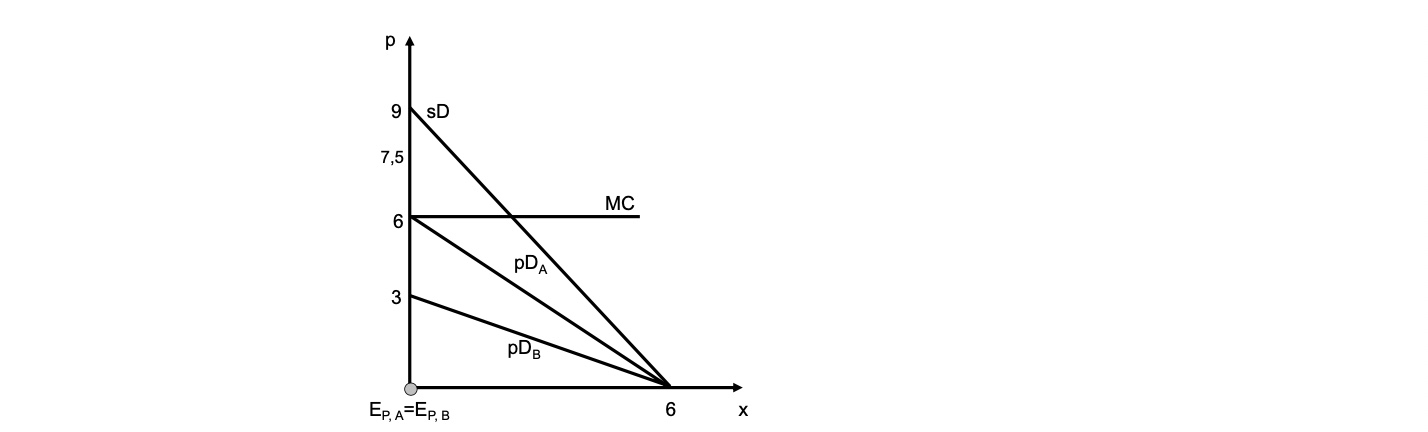
Konsumentenrente bei optimaler Menge: \(\frac{(9-6)*2}{2} = 3\)

lohnenswert für Gesellschaft => öffentliche Bereitstellung!

Trittbrettfahrer

Kosten sinken auf MC = 3

• Gemeinschaft stellt bereit: \(3 = -1.5x+9 \to x = 4\)

  • Konsumentenrente: \(\frac{(9-3)*4}{2} = 12\)

• A stellt Bereit: \(3 = -x+6 \to x = 3\)

Graphisch: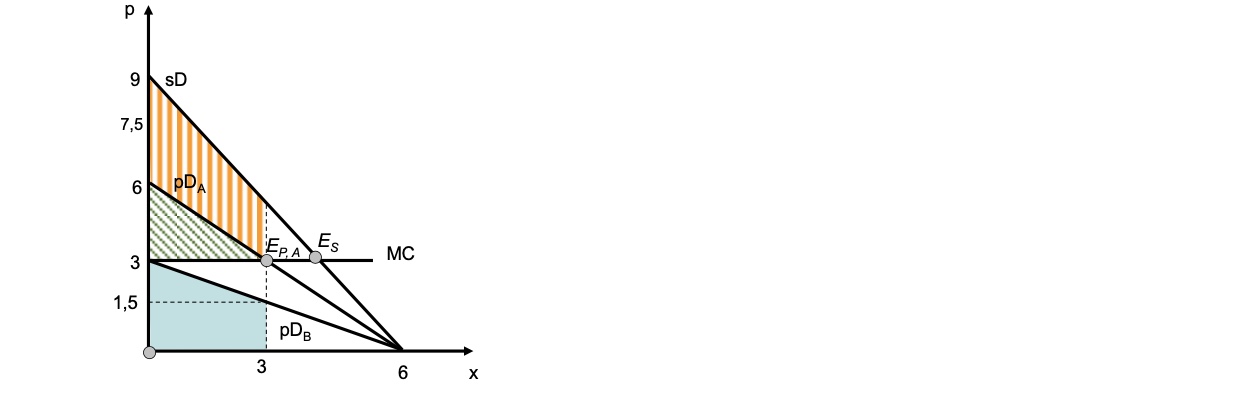

• Rente von A = grün

  • analytisch: \(\frac{(6-3)*3}{2}= 4.5\)

• Rente von B = blau

  • da er nicht von Konsum ausgeschlossen werden kann

  • Analytisch: \(\frac{(3-1.5)*3}{2}+3*1.5 = 6.75\)

• Gesamtrente = orange+grün

  • \(4.5+6.75 = 11.25; \Delta GR = 0.75\)

die nächste Einheit kostet 3€ bereitzustellen, aber keiner der Individuen erhält 3€ Rente von nächstem Gut