11.11.2021 Fibonacci

Weiterführung zu Eigenwerten

\( det(A-\lambda I) = p_n(\lambda) = 0\) -> n-tes polynom von lambda

Geomentrische Deutung der EW und EV

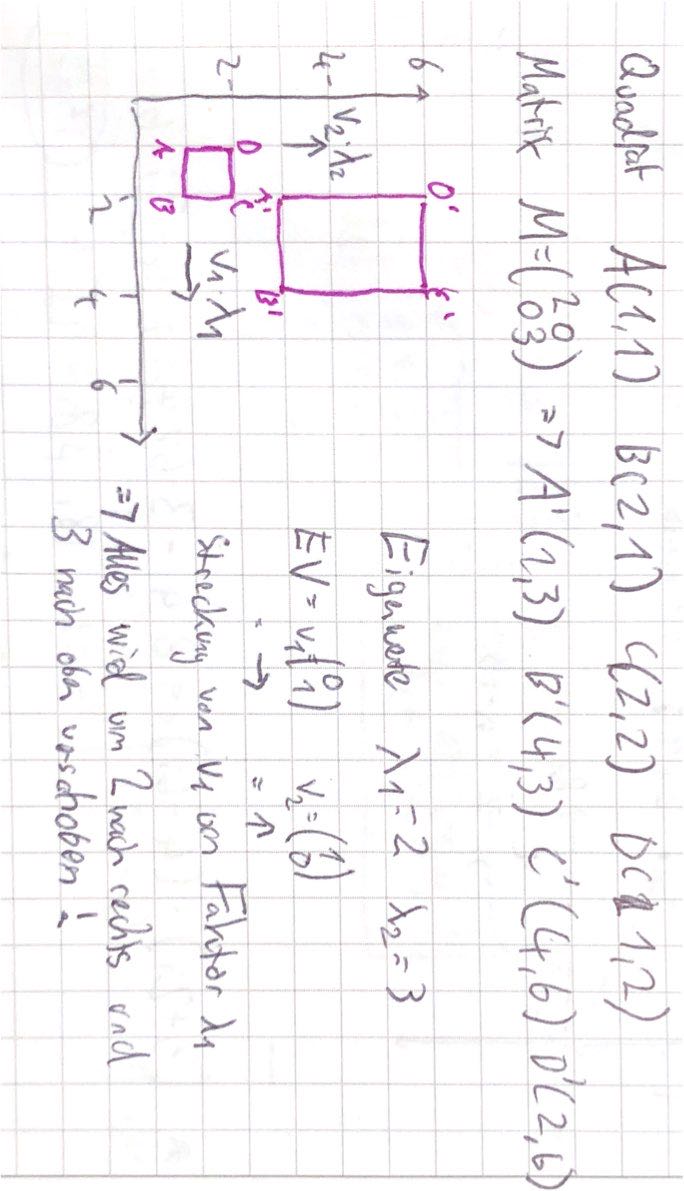
Beispiel 86

Auf einem Markt konkurrieren zu einem Zeitpunkt t = 0 zwei Produkte mit den Marktanteilen 0,3 und 0,7. Bezeichne aij = P (j → i) die Wahrscheinlichkeit, dass ein Kunde in einem Zeitschritt vom Produkt j auf Produkt i wechselt (bzw. nicht wechselt, für j = i). Die Matrix A = (aij) der Käuferfluktuation sei gegeben durch

Ausgansmatrix \(A = \left(\begin{array}{rrr} 0,75 & 0,35 \\ 0,25 & 0,65 \\ \end{array}\right)\)

Fibonacci

\( F_0 = 1; F_1 = 1 \implies F_{n +1} = F_n + F_{n-1}\)

Ausdrücken mit Matrizen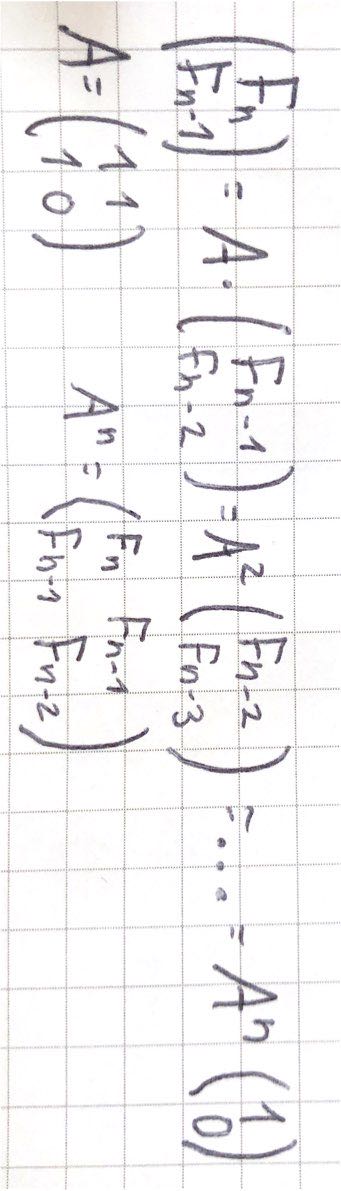

Berechnen der Potenzen von Matrizen (für \(F^n\))

Verallgemeinerte Eigenvektoren - Hauptvektoren

wenn man zu wenige Eigenvektoren hat = Problem!

Beispiel

\(A = \left(\begin{array}{rrr} 0 & 1 \\ 0 & 0 \\ \end{array}\right)\) hat Eigenwerte \(\lambda_1 = \lambda_2 = 0\)

Problem: nur ein Eigenvektor \(v = (1,0)^T\)

Sagen als: Der Eigenwert \(\lambda =0 \) hat

• algebraische Vielfachheit 2 (Anzahl Eigenwerte), aber nur

• geometrische Vielfachheit 1 (Anzahl Eigenvektoren)*

normalerweise geometrische = algebraische Vielfachheit

wenn nicht, dann Matrix nicht diagonalisierbar!

Rettung: Hauptvektor

Hauptvektor: der Vektor \(w \in \mathbb{C} \) falls \((A-\lambda I)^m w = 0\) für ein \( m \in \mathbb{N}\)

Beispiel 92:

Aber: für diese Klausur nicht relevant