19.01.2023 Erweiterungen der Spieltheorie

Nash Gleichgewicht

Beispiel Nullsummenspiel: Meetup with my Ex

• deine Ex will dich sehen, du sie aber nicht

  • Aufeinandertreffen, sie freut sich (1), du nicht (0)

• was einer gewinnt, verliert ein anderer

• kein Nash-Gleichgewicht in reinen Strategien

  • niemand findet irgendwas gut

gemischte Strategien

Voraussetzung: Spieler indifferent zwischen reinen Strategien

dann Strategien mit Wahrscheinlichkeiten versehbar

• ich gehe mit Wahrscheinlichkeit p in Harzmensa

• Ex mit Wahrscheinlichkeit q in Harz und Gegenwahrscheinlichkeit in Tulpe

indifferent: \(U(Harz) = U(Tulpe)\)

mein Nutzen dann: $\( U(H) = q \cdot 0+(1-q) \cdot 1 \\ U(T) = q \cdot 1+(1-q) \cdot 0 \)\( daraus folgt: \)1-q=q \implies q = \frac{1}{2}$

Nash-Theorem

Nash-Theorem: jedes endliche Spiel hat mindestens ein Nash-Gleichgewicht (ob rein oder gemischt)

• Aber: nicht immer herausfindbar (Schach)

Trembling Hand

Erweiterung des Gleichgewichtkonzeptes

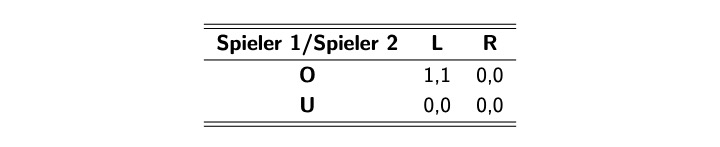
• wenn Spieler 1 denkt, Spieler 2 spielt links, dann Oben beste Antwort

• Wenn 1 denkt, 2 spielt Rechts: indifferent

• vice-versa Strategien Spieler 2

	L	R
O	(1,1)	0, 0
U	0, 0	(0, 0)

• zwei Gleichgewichte finden:

  1. Oben + Links

  2. Unten + Rechts, da eigentlich beide indifferent, aber dann trotzdem Treffpunkt

• das zweite GG ist auch GG, aber eigentlich unsinnig

Schwache Dominanz: eine Strategie dominiert andere schwach, wenn

• sie für keine Strategie des anderen Spielers schlechtere Antwort

• aber für mindestens eine Strategie bessere Antwort

• Oben und Links sind schwach dominante Strategien

• schwach dominierte Gleichgewichte sind also eigentlich nicht plausibel

Trembling Hand Gleichgewicht: Nash-GG, bei dem Strategien beste bleiben, wenn Spieler mit winziger Wahrscheinlichkeit \(\epsilon\) andere Strategie spielt (zitternde Hand)

• Oben bleibt für Spieler 1 beste Strategie, trotz eigentlich Indifferenz

• (O, L) ist Trembling Hand GG

• (U, R) ist nicht Trembling Hand GG, da Wechsel hier sich lohnt

=> jedes Trembling Hand GG ist Nash-GG, aber nicht umgekehrt

Teilspielperfekte Gleichgewichte

Erweiterung von Selten für Sequentielle Spiele: nacheinander Züge

• Darstellung meist mit Spielbaum (Extensivform)

• jeder Knoten ist aber Teilspiel

teilspielperfektes GG: Strategieprofil, das in jedem Teilspiel ein Nash-GG erzeugt

=> jedes teilspielperfekte GG ist Nash-GG, aber nicht umgekehrt

Beispiel

• wieder ObenUnten/Links Rechts, aber zuerst spielt Spieler 1

Normalform:

Spieler 1 / Spieler 2	L	R
O	(5,1)	0,0
U	2,2	(2,2)

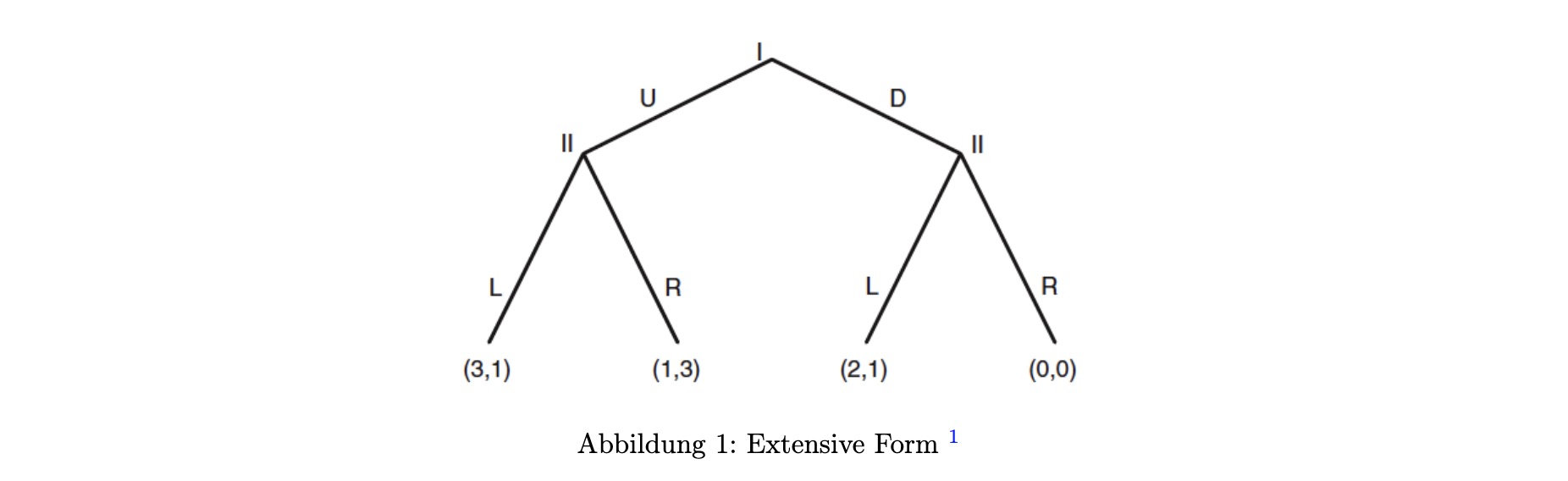
Extensivform:

graph LR A([Spieler 1]) --Oben--> B([Spieler 2]) A --Unten--> C(2, 2) B --Links--> D(5,1) B --Rechts--> E(0,0)

• Spieler 2: würde in Teilspiel Links spielen

• Spieler 1: würde Oben spielen

• also teilspielperfektes GG nur <Oben, Links>

• das andere ist nicht teilspielperfekt

die Drohung, dass Spieler 2 R spielt, ist unglaubwürdig!

Spieltheorie

• verschiedene Arten von Gleichgewichten

• aber nie Vorhersage, welches sich wirklihc einstellt

• basierend auf rationalen Annahmen

Übung

Aufgabe 4: Teilspielperfekte GG

1 / 2	LL	LR	RL	RR
U	3,1	3, 1	1, 3	(1, 3)
D	2, 1	0, 0	(2,1)	0, 0

Gleichegwichte herausfinden:

• wenn Sp1 U spielt, höchste Zahlen an zweiter Stelle markieren (durch die Zeilen gehen)

• dann wenn Spieler 2 RR wählt, höchste in jeder Spalte an erster Stelle markieren

• dann GG finden

aus diesen beiden GG würde Spieler 1 das (2, 1) wählen, also D als erste Option