25.10.2022 Konsumententheorie I#
im System der Neoklassik
Neoklassik: Wirtschaft ist System aus Märkten, in denen Angebot und Nachfrage zusammenkommen
Akteure = homo oeconomicus
nutzenmaximierend
rational
zukunftsschauend
in der Mikro = Rational Choice Theory
normative Theorie
teilweise deskriptiv/positiv = empirische Frage
axiomatische Theorie mit Annahmen
Präferenzen#
Menschen haben Präferenzen
Binär = verbindet zwei Sachen
bspw. Anna mag Äpfel lieber als Bananen
\(\succ\) = starke Präferenz: striktes Vorziehen X vor Y
\(\succsim\) = schwache Präferenz: X mindestens genauso gut wie Y \(\neq\) besser!
\(\sim\) = indifferent: X genaus gut wie Y
Präferenzen sind bezogen auf Choice Set, bspw:
A = \(\left\langle \text{2 Bananen, 3 Birnen} \right\rangle\)
B = \(\left\langle \text{3 Bananen, 2 Birnen} \right\rangle\)
Präferenzen sind vollständig und transitiv
transitiv: aus 2 Präferenzen folgt dritte\(\forall A,B,C \to A \succsim B; B\succsim C \implies A \succsim C\)
Bsp.: Relation „ist Vorfahr von“ anhand 3 Menschen
wenn A Vorfahre von B ist, und B Vorfahre von C, dann ist A Vorfahre von C
vollständig: wenn für alle Elemente eine Relation festgelegt ist
außerdem Bedingungen:
Nichtsättigend: mehr ist immer besser
konvexität: Mischung aus Güter ist besser als nur ein Gut (bei gleichem Nutzen)
stetig: keine Sprünge zwischen ähnlichen Bündeln
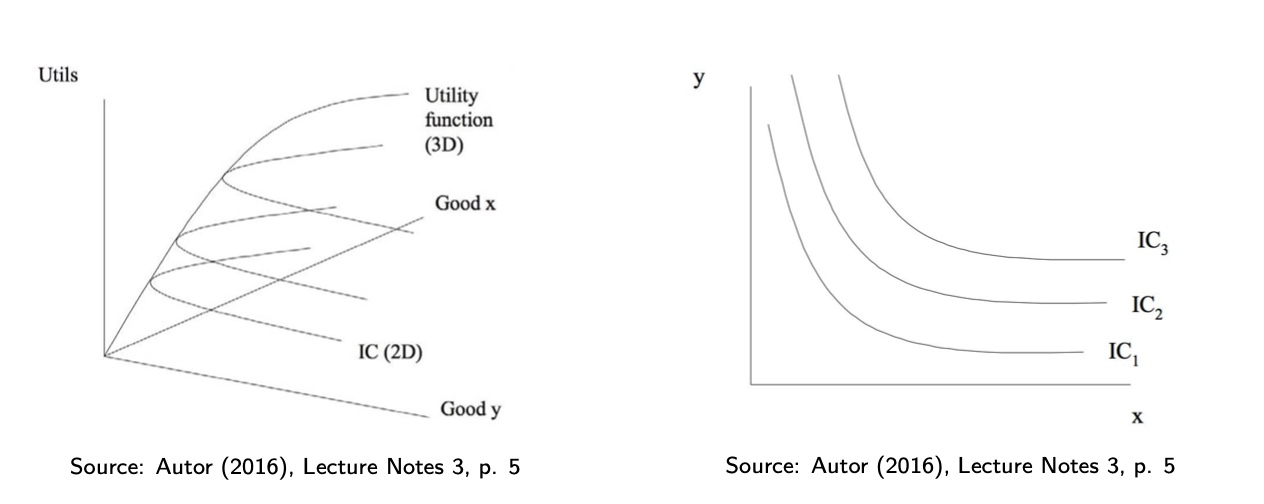
Nutzenfunktion#
Nutzenfunktion: mathematische Beschreibung zur Beschreibung von Präferenzrelationen
Nicht Werte der Funktion interpretieren! (nur kardinal, nicht ordinal)
werden durch Indifferenzkurven visiualisiert
gleiche Kurve = gleicher Nutzen
unendlich viele Kurven
sind konvex
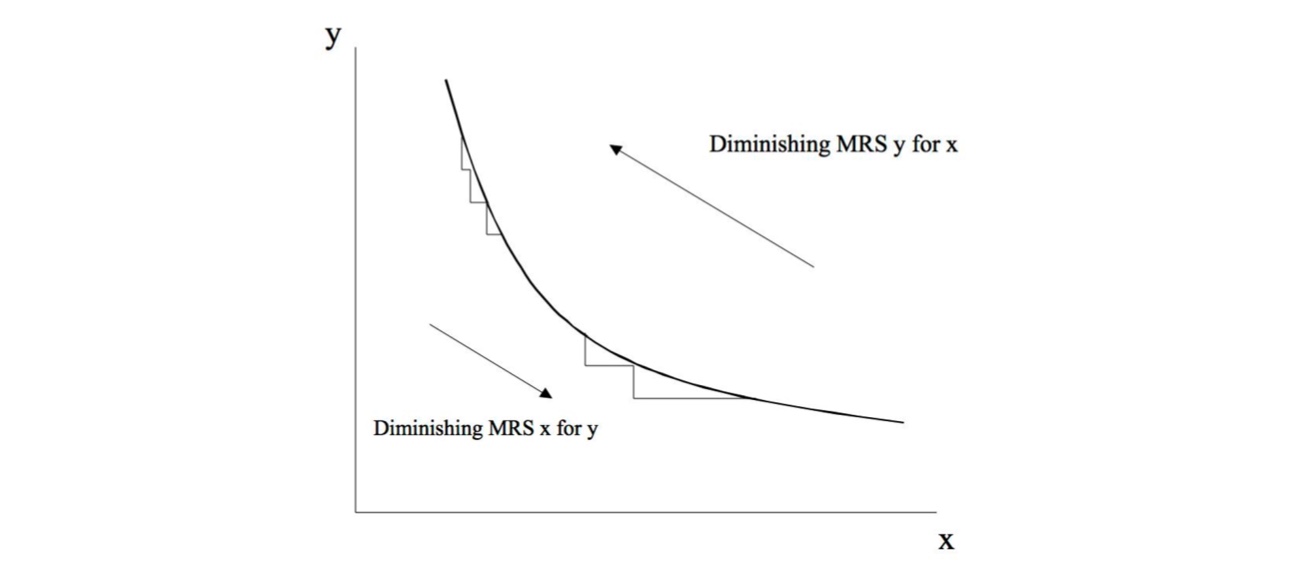
Grenzrate der Substitution#
Bereitschaft, auf Einheiten von Gut x zu verzichten, um Gut y zu erhalten
= Steigung der Indifferenzkurve
$\(
-\frac{dy}{dx} = \frac{MU_x}{MU_y}
\)$
Übung#
Aufgabe 2: zutreffende Implikationen
wenn \(x \succ y \; \& \; y \succ z \implies x \succ z\)
wenn \(x \succsim y \; \& \; y \succ z \implies x \succ z\)
wenn \(x \succsim y \; \& \; y \succ z \implies x \succsim z\)
wenn \(x \succ y \; \& \; y \sim z \implies x \succ z\)
wenn \(x \sim y \; \& \; y \sim z \implies x \sim z\)
wenn \(x \succsim y \; \& \; y \succsim x \implies x \sim y\)