26.11.2021 Lineare Optimierung 1

Elementare Basistransformation

Lösen eines Gleichungssystems A x = b mit x* als Lösung

Schritte zur Lösung der Gleichung:

• Hilfsmittel y einführen => \(A x + I y = b\) (viele zusätzliche Variablen)

  • wenn y = 0 -> x* ist Lösung

  • wenn x = 0 -> y = b

• Umformung zu \(I x + \tilde{A}y = \tilde{b}\) mit Austaschverfahren

  • wenn y = 0 -> x* ist Lösung

---

Beispiel Austauschverfahren: n = m = 3

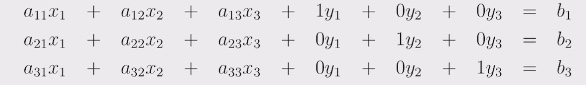
in Tabellenform: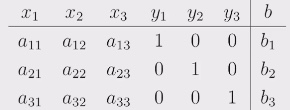

und Kurzform: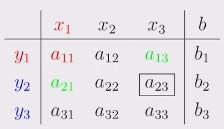

Ziel :

Schritte für jede Zeile:

1. \(I \to I/a_{11}\)

2. \(II \to II-a_{21} * I/a_{11}\)

3. \(III \to III - a_{31}*I/a_{11}\)

Ergebnis: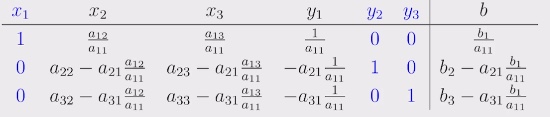

in Kurzform: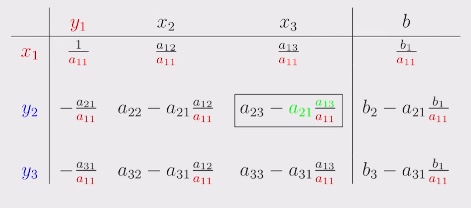

Schritte der Verkürzung von Langform auf Kurzform

Beschreibung	formal	Beispiel
Pivotelement suchen und durch 1 teilen	\(z \to 1/z\)	\(a_{11} \to 1 / a_{11} \)
Pivotzeile / Pivotelement	\(a_{il} \to a_{il} / z\)	\(a_{12} \to a_{12} / a_{11}\)
Pivotspalte / Pivotelement und dann negativ	\(a_{kj} \to -a_{kj}/z\)	\(a_{21} \to -a_{21}/a_{11}\)
auf restliches Rechteckregel (wie grün dargestellt oben)	\(a_{kl} \to a_{kl} - a_{il} a_{ki} / z \)	\(a_{23} \to a_{23} - a_{21} a_{13} / a_{11} \)

---

Anwendungsbeispiel 105: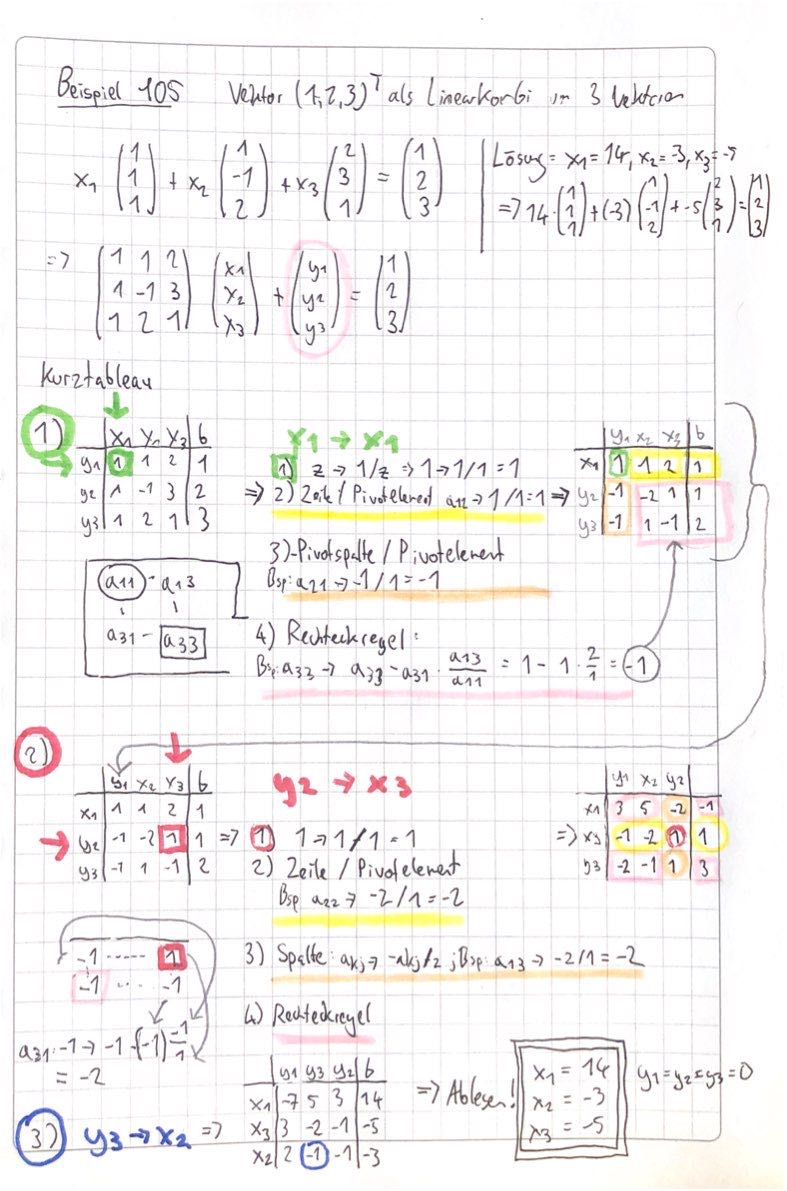

Bemerkungen:

• Inverse kann mitberechnet werden aus der Mitte der Tabelle dann!

  • aufpassen Reihenfolge Zeilen und Spalten!

• Vektor b behandelt wie A => mehrere rechte Seiten können mit