05.11.2021 Häufigkeiten#

kumulierte Verteilung#

anders als bisherige Darstellungen diesesmal: kumulierte Häufigkeitsverteilung

kumulierte Häufigkeitsverteilung: Berechnung der Anteile Ober/unterhalb einer bestimmten Grenze (bspw Armutsgrenze)

Allgemein Merkmal X:

  • n Beobachtungen, Werte: x1, … ,xn

  • zu jedem x: Anteil der Werte, die kleiner/gleich x ist => empirische Verteilungsfunktion von X

    • \(F(x) = \sum_{j:a_j\leq x}\)

    • F(x) = Anteil der Beobachtungen kleiner gleich x

empirische Verteilungsfunktion: \(F(x) = \sum_{j:a_j\leq x} mit \ 0\leq F(x) \leq 1\)

lesen als F(x) = Anteil der Beobachtungen kleiner gleich x

Beispiel:#

21-11-05_12-59

Graphische Darstellung:

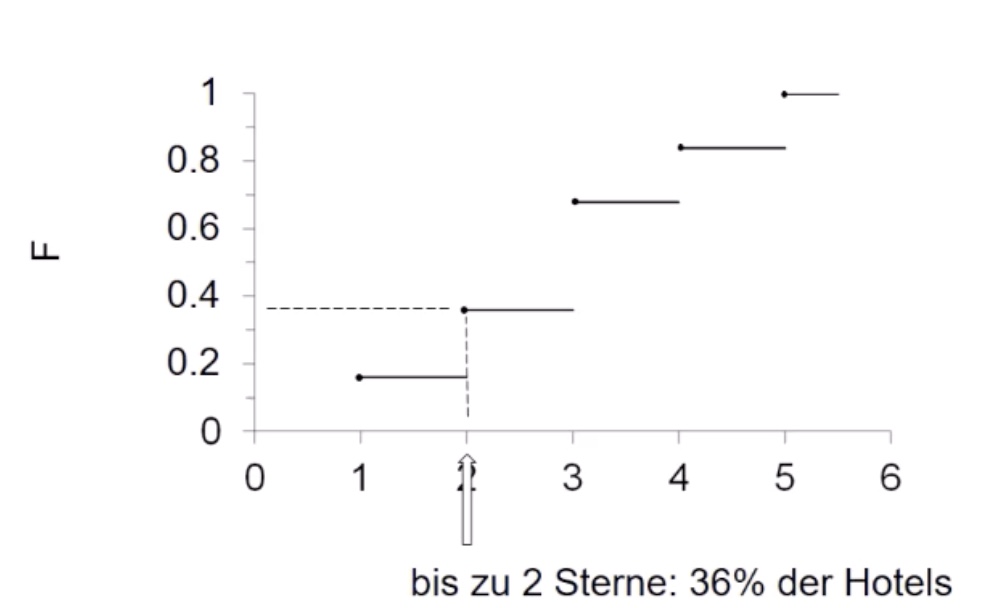
21-11-05_13-04

Review: graphische Darstellungen#

Stab-, Säulen-, Balken-, Kreisdiagramm: nominal und ordinal skalierte Merkmale

Histogramm: metrisch skalierte (stetige) Merkmale , klassiert

Statistische Kenngrößen#

erlauben Zusammenfassung von Verteilung auf einzelne Zahlen

Arten: Lage, Streuung, Schiefe, Konzentration

arithmetisches Mittel („Durchschnitt“)#

benötigt metrisch skalierte Merkmale

Notation: \(\bar{x} = \frac{1}{n} \sum^n_{i=1} x_i\) (beachte x-quer)

Beispiel aus Absolventenstudie : Merkmal Studiendauer

21-11-05_13-41

Bei Zusammefassung von arithmetischen Mitteln immer die Stichprobengröße/Gewichtung beachten!

geometrisches Mittel#

braucht metrische Merkmale > 0

für Wachstumsraten / relative Änderungen gut

Beispiel:

  • Zeit t=1 ; Wert x1=10

  • Zeit t=2 ; Wert x2=16

  • Zeit t=3 ; Wert x3=20

  • Wachstumsfaktor t=1 bis t=2 : 16/10 = 1.6

  • Wachstumsfaktor t=2 bis t=3 : 20/16 = 1.25

=> durchschnittliches Wachstum beider Zeiträume = geometrisches Mittel

Berechnung: \( 1.6 * 1.25 = 2 \implies \bar{x}_{geom} = \sqrt{2}\)

Notation: \(\bar{x}_{geom} = \sqrt[n]{x_1*...*x_n}\) (Wachstumsfaktoren multiplizieren und die Wurzel mit Anzahl der Faktoren ziehen)