14.04.2022 Effekte und Schocks#

Einkommenseffekte#

  • Ausgangsgleichgewicht mit Budgetgerade \(B_1\)

  • nun eine Einkommenserhöhung mit Budgetgerade \(B_2\)

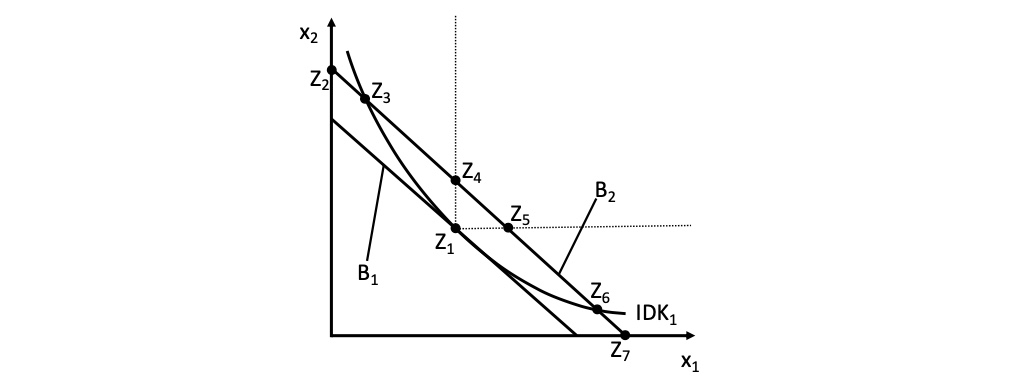
2022-04-18_11.15.01

Bereich zwischen \(Z_4\) und \(Z_5\) ist rationale neue Güterkombination

  • da nicht weniger Mengen eines Gutes als im Ausgangsequilibrium logisch

  • außer wenn ein Gut inferior ist

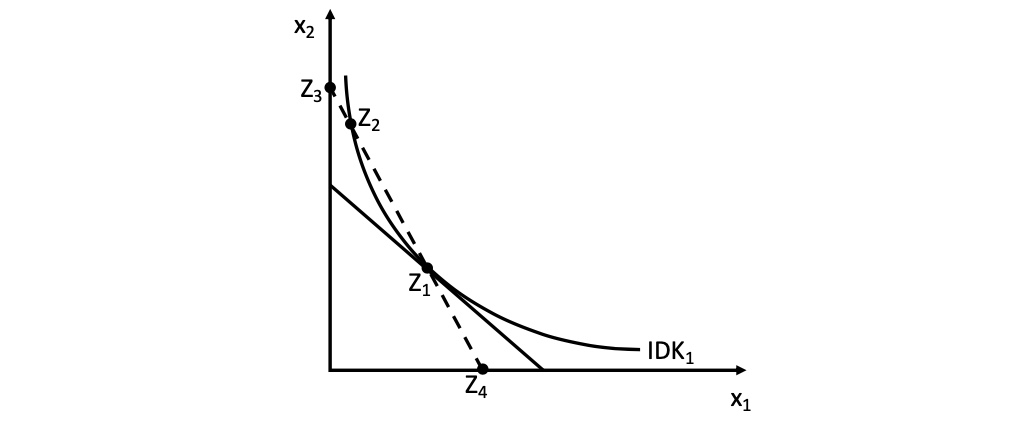
Substitutionseffekt#

Effekt einer Marktpreisänderung (gestrichelte Linie)

  • \(x_2\) wird billiger

  • \(x_1\) wird teurer

2022-04-18_11.26.58

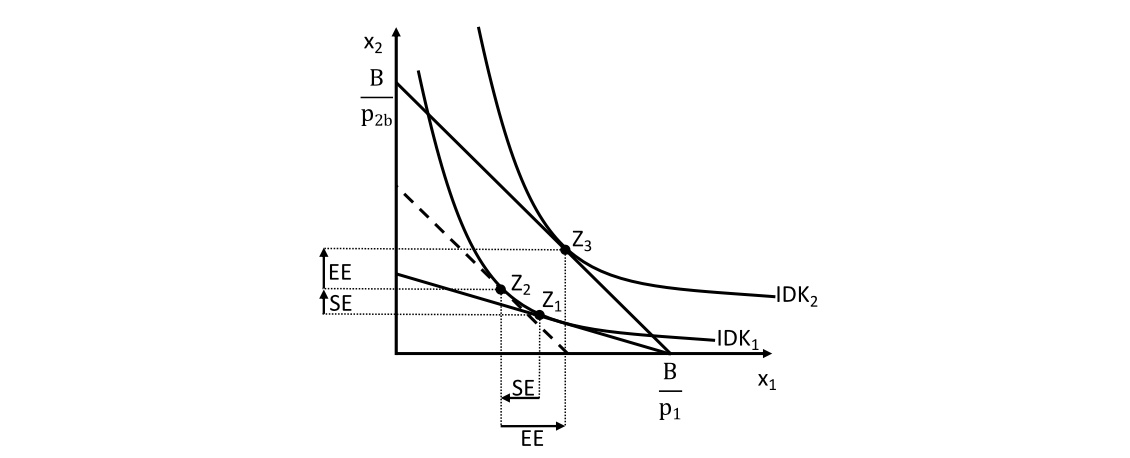
Zerlegung nach Slutsky#

nun Zerlegung der Veränderung in Einkommenseffekt und Substitutionseffekt

Ausgangslage:

  • \(IDK_1\) mit original Budgetgerade (grün)

  • Preiserlass bei \(x_2\) => Verschiebung der Budgetgeraden (schwarz) mit \(IDK_3\)

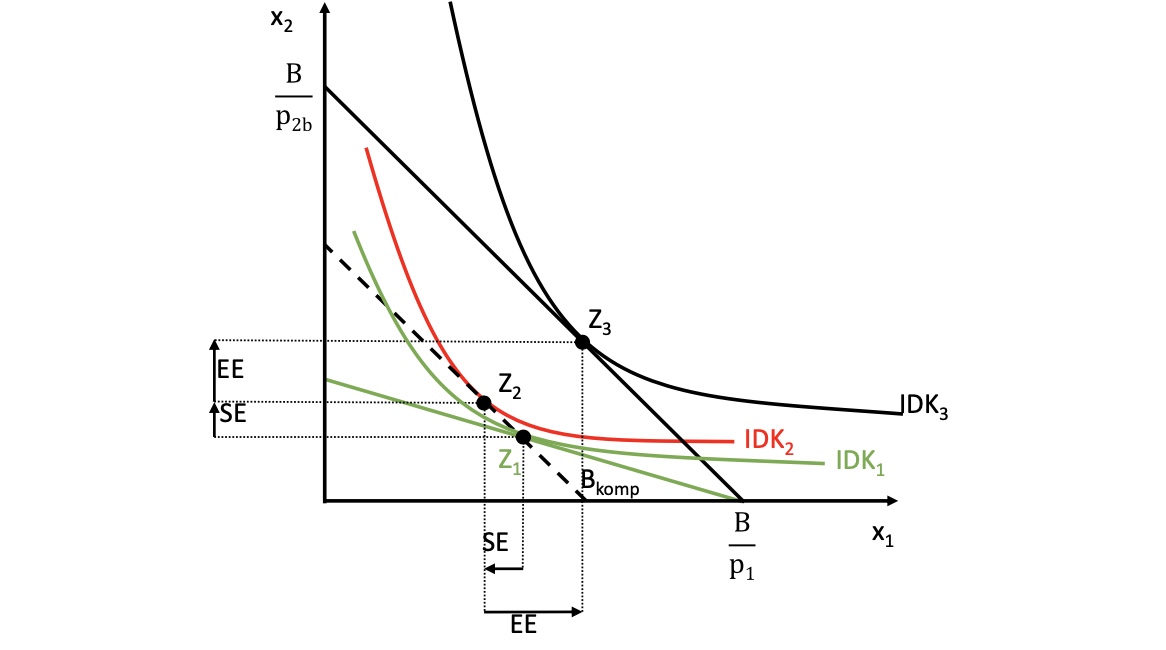
2022-04-18_11.42.13

  • Durch Verschiebung der neuen Budgetgeraden zurück auf altes Optimum

    • und neue \(IDK_2\)

    • dedeutet dass neues Preisverhältnis, aber ohne einen Einkommenseffekt

  • denknotwendig, dass Senkung von \(P_2\) zu Erhöhung nachgefragter Menge \(x_2\) führt

=> Substitutionseffekt immer negativ!

im Sinne von Preiserhöhung -> niedrigerer Konsum

Zerlegung nach Hicks#

statt Verschiebung Budgetgeraden Verschiebung IDK bis sie Ausgangsoptimum berührt

2022-04-18_11.53.58

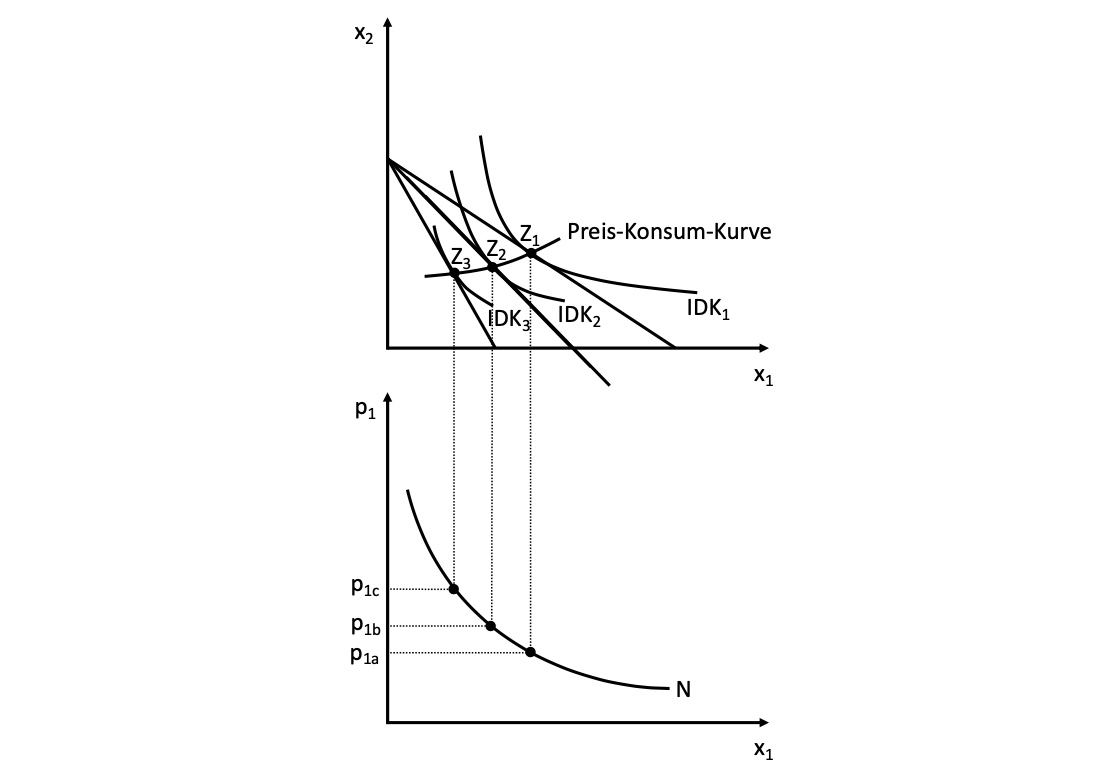
Individuelle Nachfragekurve#

durch Variation eines Gutes verschiedene Budgetgeraden und IDKs bestimmen

2022-04-18_11.57.37

Marktnachfrage#

Aggregation der invividuellen Nachfragekurven zu Marktnachfrage

durch horizontale Addition: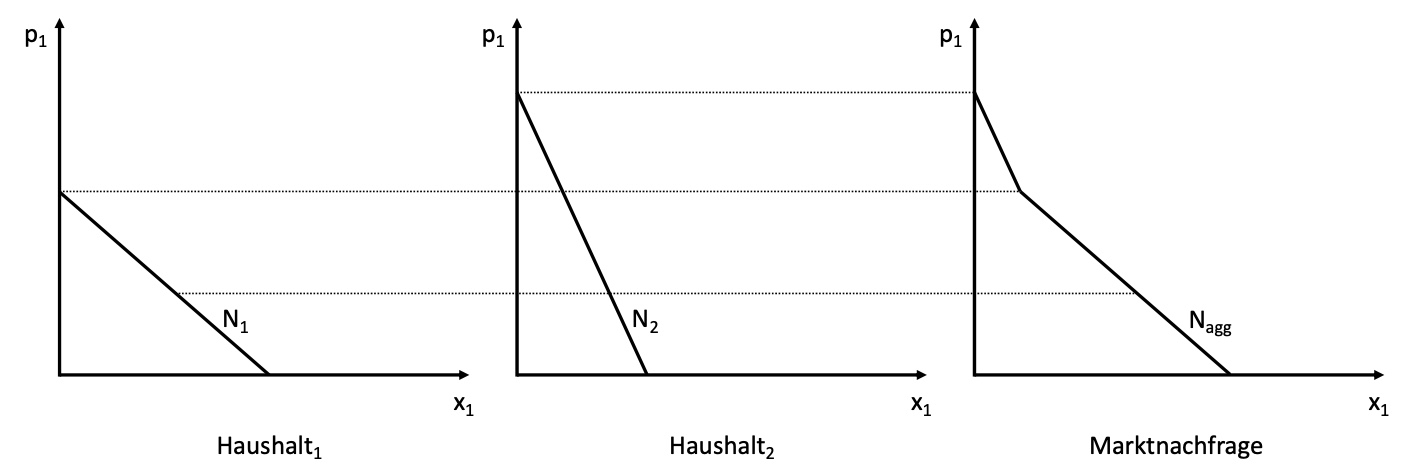2022-04-18_11.59.32

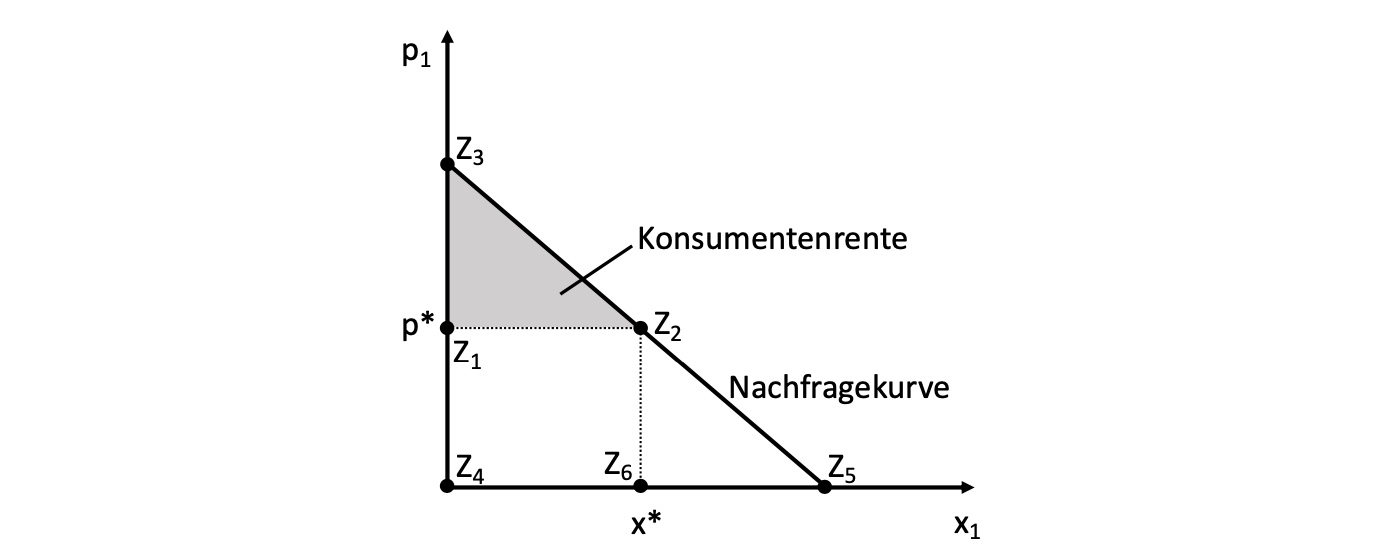
Rente#

Rente: Vorteil einer Leistung ohne Gegenleistung (wie bei Rentnern)

in der Mikroökonomik Konsumenten- und Produzentenrente

Konsumentenrente: die Summe aller individuellen Zahlungsbereitschaften der zum Zuge kommenden Nachfrager den tatsächlich gezahlten Preis übersteigt

misst Wohlfahrt, den ein Konsument erfährt, weil etwas billiger ist als er sowieso zahlen würde

2022-04-18_12.12.38

Elastizität#

Notation: $\( \epsilon_{x,p} = \frac{\Delta x \%}{\Delta p \%} \\ Umformung: = \frac{ \frac{\Delta x}{x} }{\frac{\Delta p}{p}} = \frac{ \Delta x}{\Delta p} * \frac{p}{x} = \frac{ \delta x}{\delta p} * \frac{p}{x} = \frac{\frac{p}{x}}{\frac{\delta p}{\delta x}} \)$ Elastizität ist dimensionslos!

Beispiel: 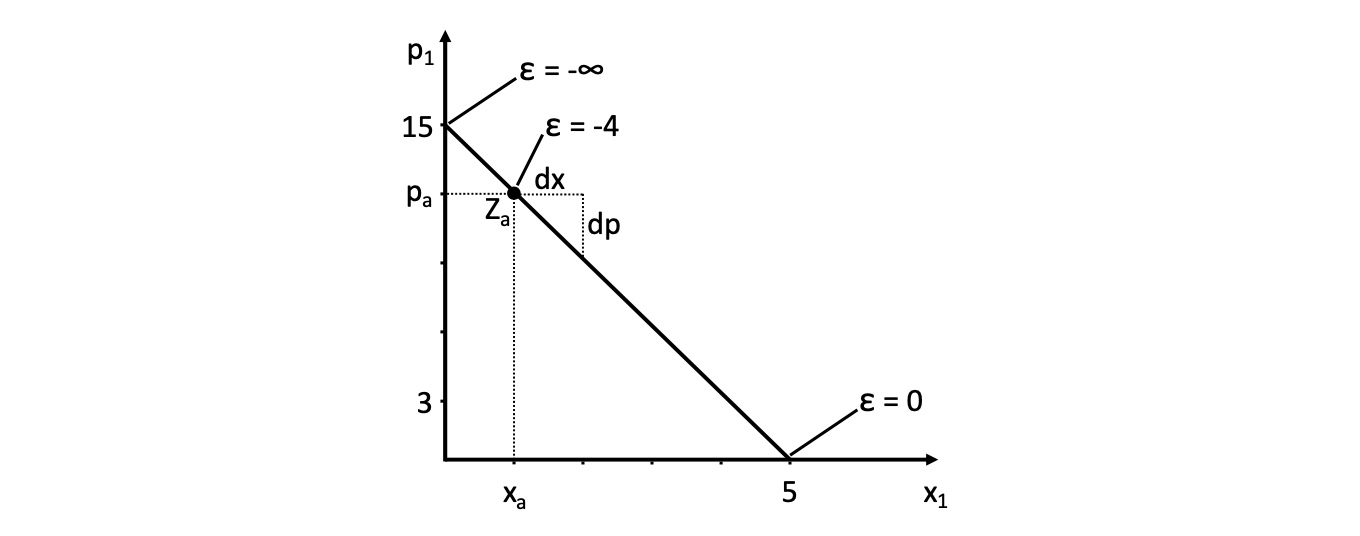2022-04-18_12.25.05

Interpretation von \(\epsilon = -4 \to\) 1% Preisteigerung => 4% Mengenreduktion

Allgemeine Interpretation:#

je höher \(\epsilon\) , desto sensibler sind Haushalte auf Preisänderungen

Wertbereiche

Interpretation

\(\epsilon = 0\)

vollkommen unelastisch

\(0 < \epsilon < 1\)

relativ unelastisch

\( 1 \le \epsilon < \infty\)

relativ elastisch

\(\epsilon = \infty\)

vollkommen elastisch

Extremfälle: 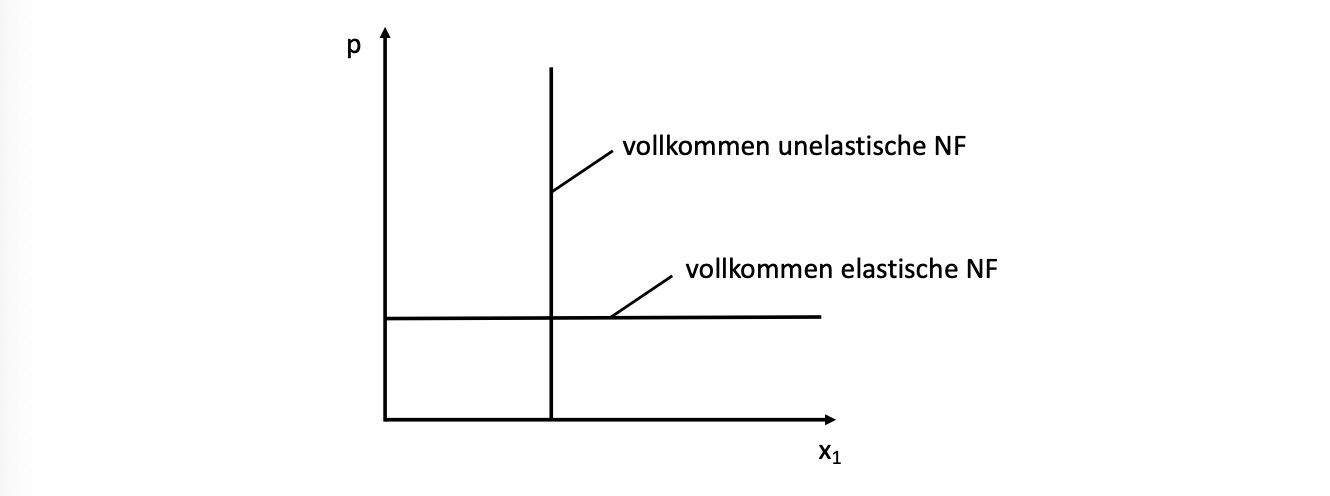2022-04-18_12.40.20

Übung#

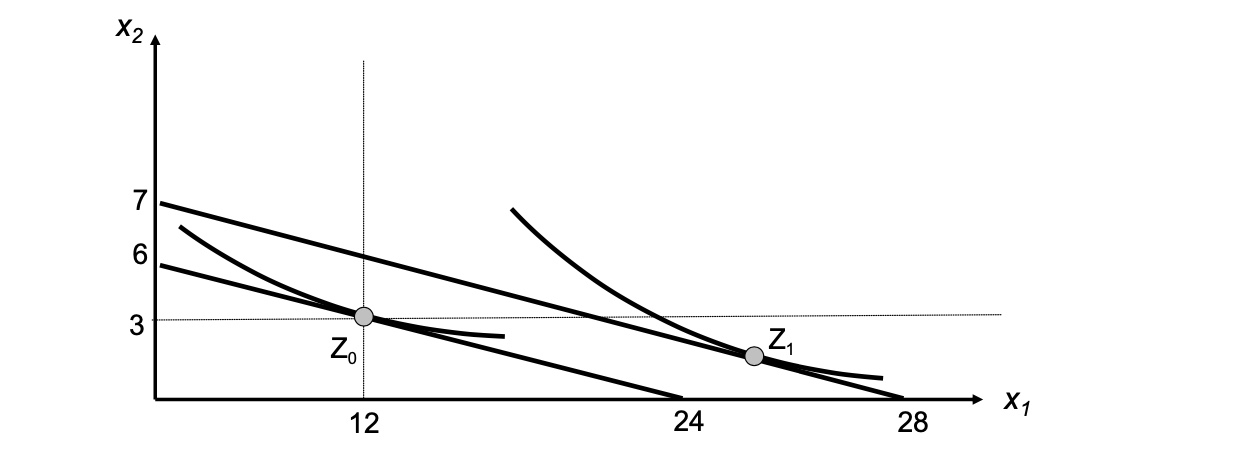
Effekt von Einkommenserhöhung bei normalen Gut \(x_1\) und inferiorem Gut \(x_2\)

2022-05-02_11.19.55