09.12.2021 Simplexverfahren II#
uneindeutige Lösung#
z-Zeile hat 0 => uneindeutige Lösung im Simplexverfahren !
BSP 133: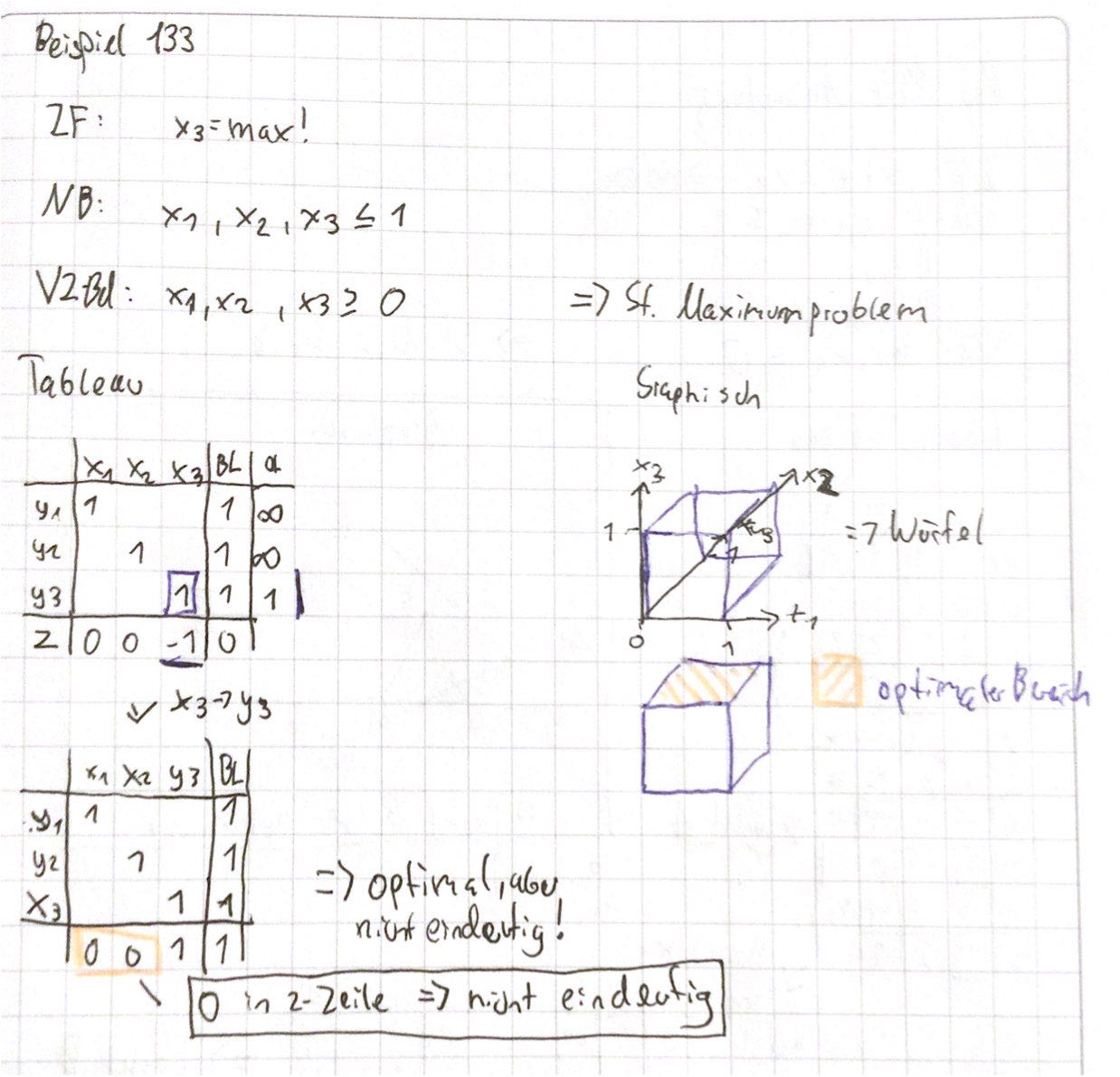
Ausartung#
Ausartung: einmaliges Festhängen des Simplexverfahrens aufgrund einer 0 in der Basislösung
BL hat eine 0 => **Ausartung! **
BSP 134: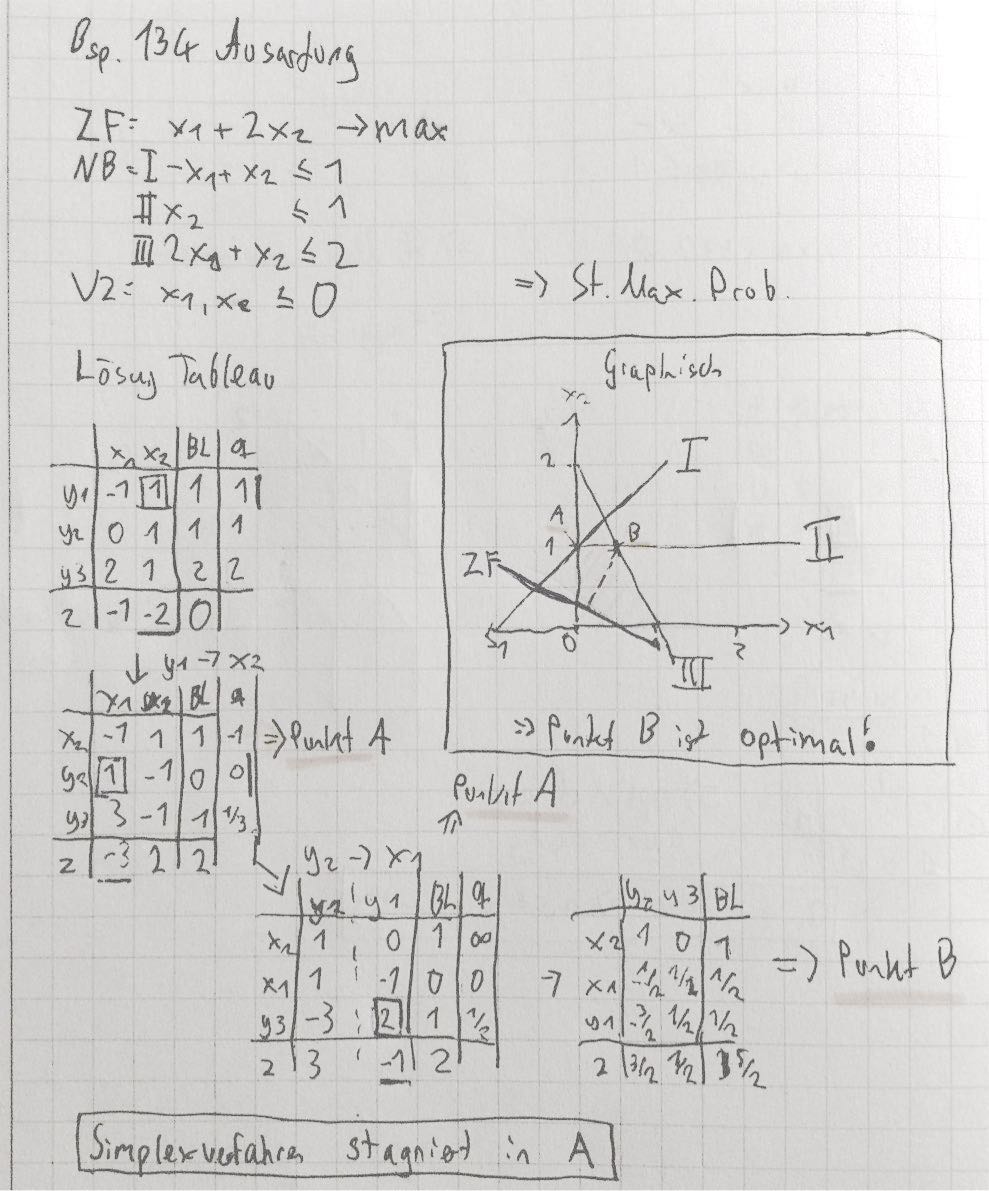
hier : Ecke A ist ausgeartet, da Schnittpunkt von \(I, II, und \ x_2\)
Ungleichung 2 ist überflüssig , der Algorithmus bleibt in dieser Ecke hängen
die 0 in der BL führt bei Rechteckregel zu keiner Veränderung (wenn in Pivotzeile)
unbeschränkter Zielbereich#
Bsp 135: 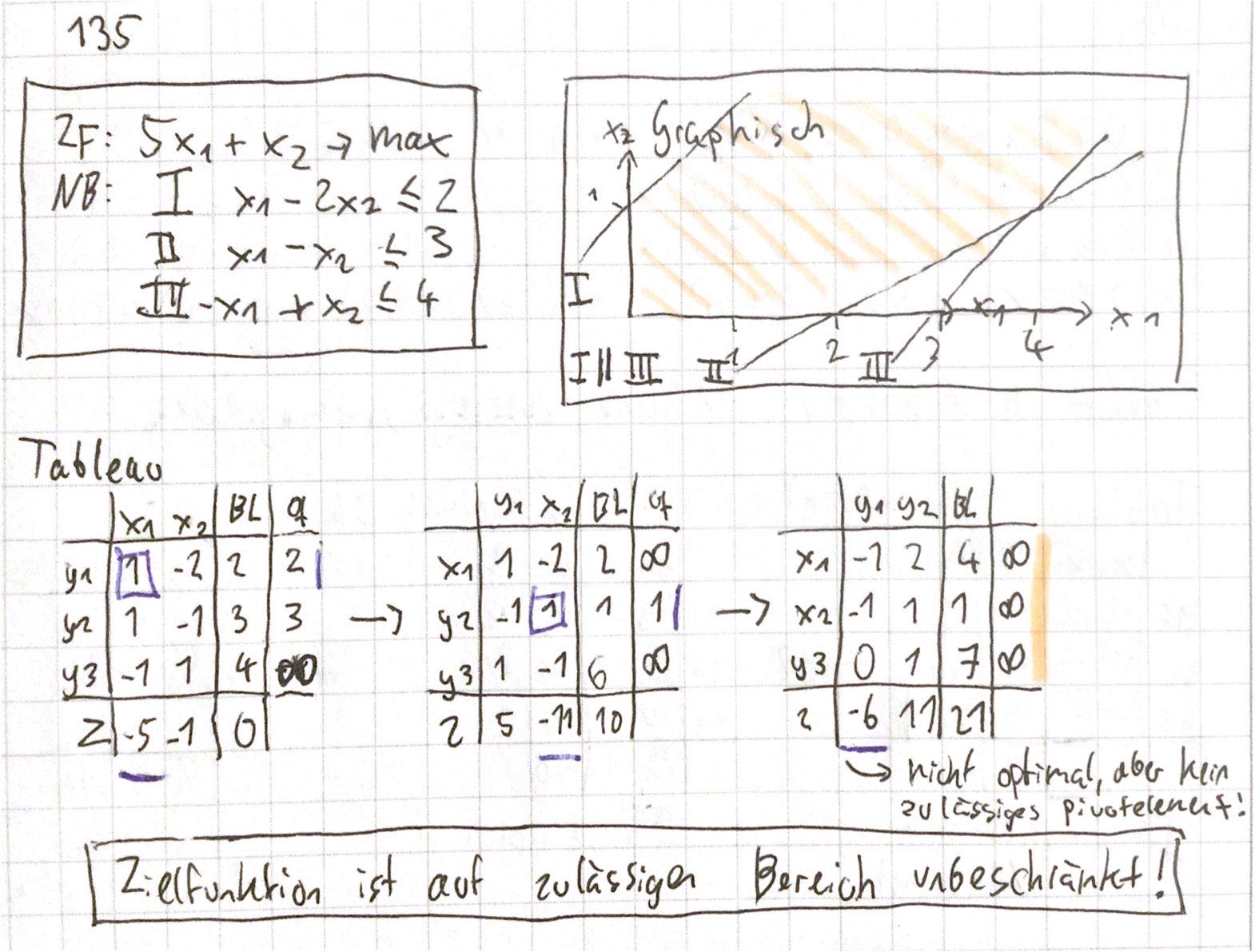
hier : Zielbereich ist unbeschränkt!
\( I || III \) beide Geraden sind parallel
leerer Zielbereich#
Tableau ist optimal, aber Zielwert ist negativ => leere Zielmenge/unzulässig
Regeln Pivotelementauswahl#
in z-Zeile niedrigsten Wert nehmen => (höchster negativer Betrag)
\(BL-Spalte / ausgewaehlte \ Spalte = q\) => niedrigster Wert
Werte von q die negativ sind = verboten
Werte von q die 0 sind = verboten
außer wenn entstehendes Pivotelement nicht 0 ist
Treffpunkt von beiden niedrigsten Werten => Pivotelement
Pivotelement muss > 0 sein (positiv)
Minimumprobleme#
Erinnerung Standardmaximumproblem:
Zielfunktion: \(max \ c^Tx \)
Vorzeichen: \(x_i \ge 0\)
Ungleichungen: \( Ax \le b\)
\( b \ge 0\)
Umformung eines Minimumproblems zu einem SMP
ZF: \(x_1 - x_2 = min \implies -x_1+x_2 = max\)
VZ: \(x_i \implies \tilde{x_i} - \bar{x_i}\)
\(Ax \ge b * (-1) \implies -Ax \le -b\)
letzte Bedingung = kritisch! , da wichtig für Anfangsecke
Bsp: 109 