29.11.2021 Schiefemaße + Konzentrationsmaße

Schiefe

Charaktersierung der Symmetrie einer Häufigkeitsverteilung

Kategorien:

• links / rechts

• schief / steil

Beispiel: linksschief + rechtssteil = Anstieg auf linker Seite, starker Abfall rechts

Daumenregel: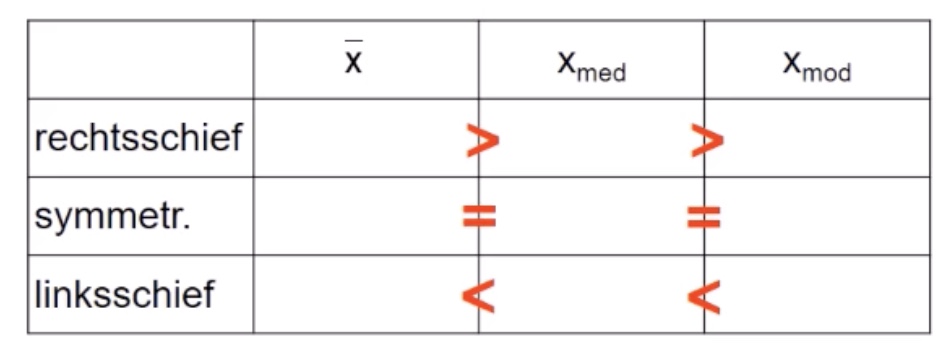

Schiefekoeffizient

\[ g_m = \frac{ \frac{1}{n}*\sum_{i=1}^{n} (x_1 - \bar{x})^3 } {\left( \sqrt{\frac{1}{n}*\sum_{i=1}^{n} (x_1 - \bar{x})^2} \right)^3} \]

• Symmetrisch: \(g_m = 0\)

• rechtschief: \(g_m > 0\)

• linksschief: \(g_m < 0\)

Konzentration

wie sind Ausprägungen auf Objekte verteilt? Oder: wer hat wieviele Kekse? :cookie:

Lorenzkurve

graphische Darstellung der Konzentration

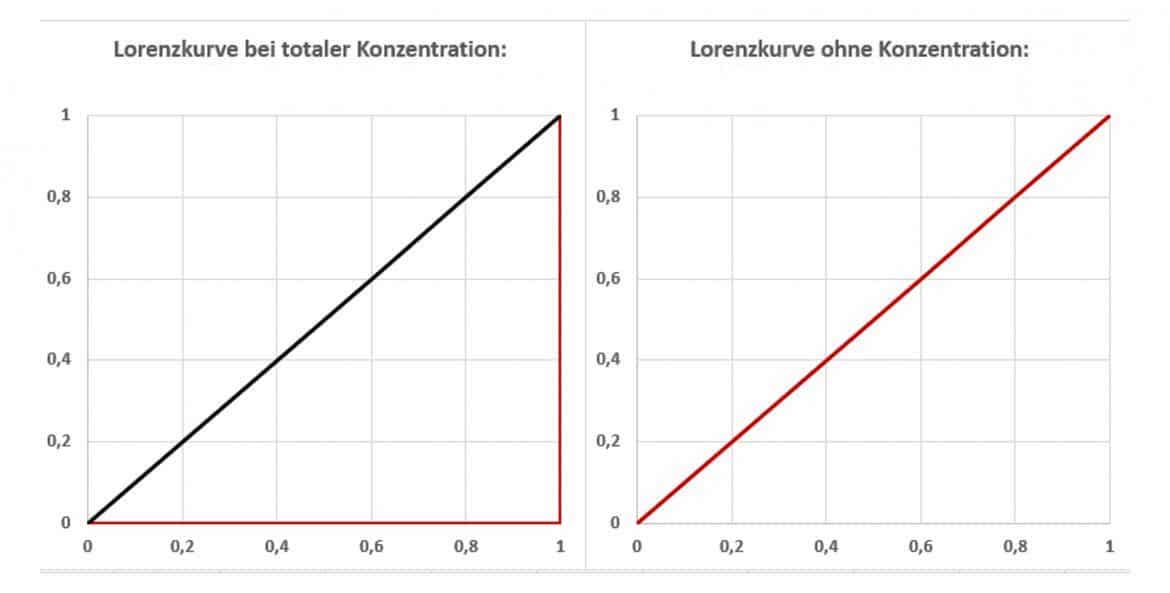
Voraussetzung: Urliste X kardinal skaliert

1. \(x_{(1)},...,x_{(n)}\) ordnen

2. \(f_i = \frac{1}{n}\) berechnen

Lorenzkurve = Graph durch \((u_0,v_0),...,(u_n,v_n)\) mit

• x-Achse: kumulierter Anteil der Merkmalsträger

  • \(u_q = \sum_{i=1}^q f_i\) , also q-te Koordinate auf u-Richtung i

• y-Achse: kumulierter Anteil der Merkmalsmenge

  • \(v_q = \sum_{i=1}^q \tilde{v}_i\) mit \(\tilde{v}_q = \frac{x_{(q)}}{\sum xi}\)

Eigenschaften der Lorenzkurve:

• monoton wachsend

• Konvex (nach unten hängende Wölbung)

Ausmaß der Konzentration: Fläche zwischen Hauptdiagonale und Lorenzkurve => Gini-Koeffizient

Gini-Koeffizient

G = Fläche zwischen Diagonale und Lorenzkurve / Fläche zwischen Diagonale und Achse

Formal: \(G = \sum(u_{i-1}+u_i) * \tilde{v}_i - 1\)

Eigenschaften:

• Obergrenze variiert mit n

---

Beispiel

Monatlicher Umsatz von 5 Möbelhäusern in einer Stadt

Haus	Umsatz	\(q\)	\(f_q\)	\(u_q\)	\(x_{(q)}\)	\(\tilde{v}_q\)	\(v_q\)
1	60	1	0.2	0.2	20	20/200	20/200=0.1
2	50	2	0.2	0.4	30	30/200	50/200=0.25
3	40	3	0.2	0.6	40	40/200	90/200=0.45
4	30	4	0.2	0.8	50	50/200	140/200=0.7
5	20	5	0.2	1.0	60	60/200	1
\(\sum\)					200

1. \(q \to f_q\) : Kumulieren

2. \(u_{q}\) = in dem Fall das Gleiche wie f

3. \(x_{(q)}\) = absteigend sortierte Merkmale und summieren

4. \(\tilde{v}_q = x_{(q)} / Summe\)

5. \(v_q = kum \ \tilde{v}_q\)

Lorenzkurve: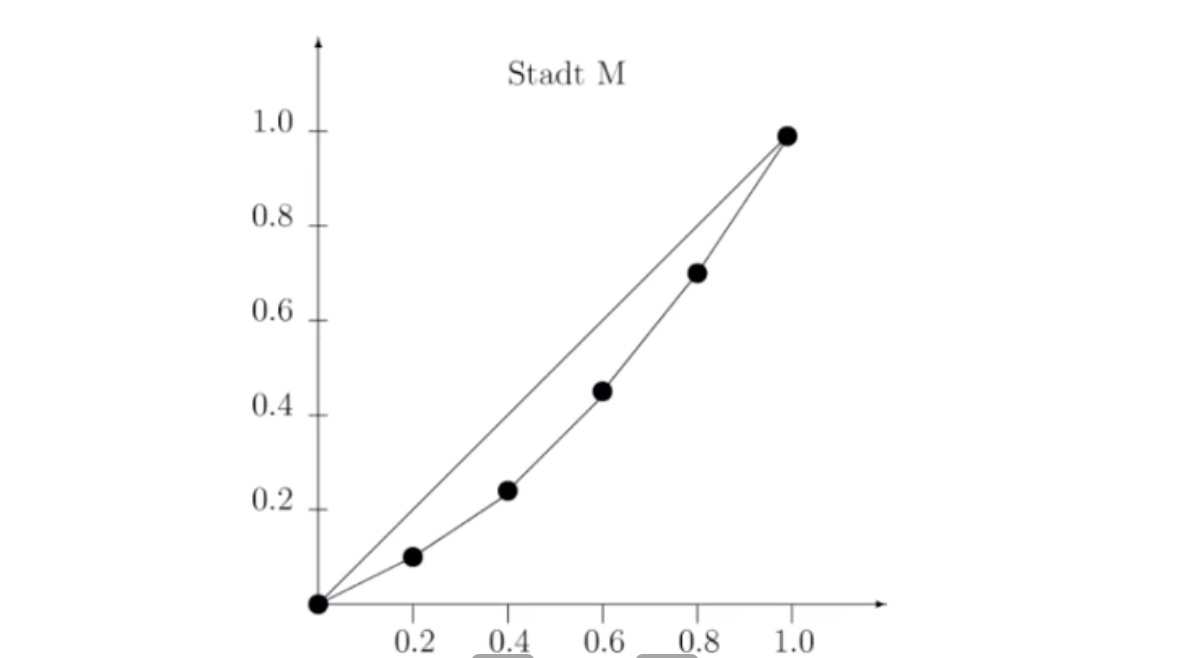

Gini-Koeffizient = 0.2

---

Absolute Konzentrationsmaße

öndert sich abhängig von der Anzahl der betrachteten Objekte

Herfindahl-Index

• Berechnung: \(H = \sum \tilde{v}^2_i\)

• mögliche Werte: 1/n < H < 1

• Nutzung: Marktanalyse H > 0.25 = extreme Marktkonzentration