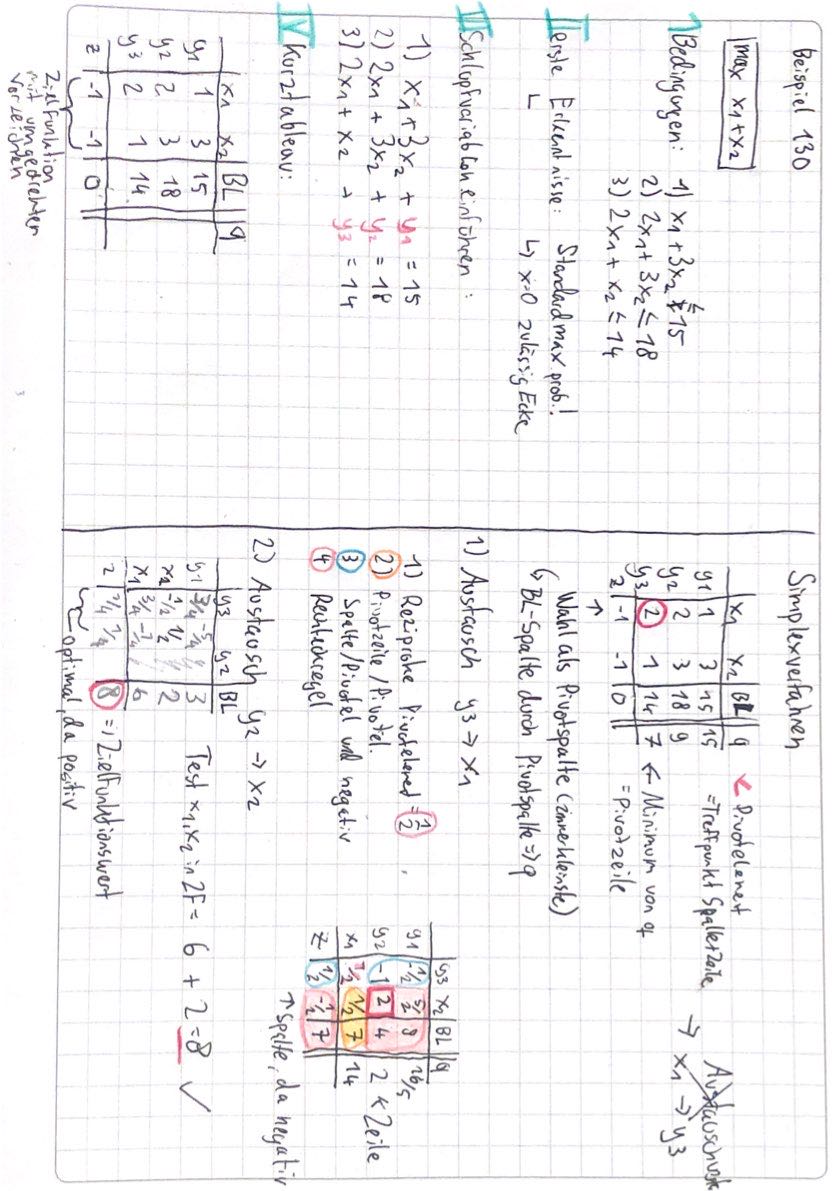
30.11.2021 Simplexverfahren

Seiten

vorige Feststellungen: im graphischen Verfahren => optimale Lösung in Ecke (von zwei Seiten)

Seite (verallgemeinert!): eine Menge F mit \(F = \{x \in Polyeder: A'x = b'\}\), also ein Teilsystem der Ungleichungen, die das Polyeder beschreiben

Ecke: ist eine verallgemeinerte Seite mit eindeutiger Lösung des Teilsystems

Genauer: x ist Ecke, wenn m lineare unabhängige Zeilen mit Gleichheit erfüllt sind

Konvexe Funktion

konvexe Funktionen: der Funktionsgraph verläuft unter allen Sekanten, d.h jede Verbindungsstrecke zweier beliebiger Punkte liegt über der Funktionslinie

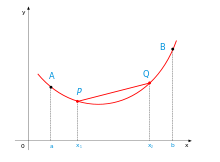
• Mathematisch: \(f(\alpha_1 a + \alpha_2 b) \le \alpha_1 f(a) + \alpha_2 f(b)\) mit \(\alpha_1 + \alpha_2 =1\)

• oder auch: zweimal ableitbar und Ergebnis >= 0

Simplexverfahren

Typen von Ungleichungssystemen:

1. \(Ax \le b\)

2. \(Ax \le b, x\ge 0\) (häufigste)

3. \(Ax = b, x \ge 0\)

Standardmaximumproblem: (SMP) Form des linearen Optimierungsproblems (LOP) mit Ziel der Maximierung der Funktion in der Form \(max \ c^T \ mit \ Ax \le b; x \ge 0, b \ge 0\)

Eigenschaften eines LOP:

• nicht lösbar: wenn zulässiger Bereich leer oder

  • Zielfunktion unbeschränkt in Bereich (unendlich offener Bereich)

• lösbarwenn zulässiger Bereich beschränkt ist

  • dann Lösung in einer Ecke des Bereichs

Merke: Ecke x=0 ist bei Standardmaximumproblem (SMP) erlaubt und hat Zielfunktionswert \(z_0\)

Idee des Simplexalgorithmus:

1. Phase: zulässige Ecke bestimmen (bei SMP Nullecke) und Kurztableau erstellen

2. Phase: schrittweise Verbesserung von \(z\) durch Ablaufen Ecken

zu 1:

zu 2:

1. Wahl der Austauschspalte: Minimum in der untersten Zeile => Spalte j

2. Wahl Austauschzeile: Spalte der Basislösung durch Austauschspalte dividieren = Spalte q

   • Minimum in q => Spalte i

3. Pivotelemente: Element im Schnittpunkt von Spalte j und Zeile i

4. Austausch mithilfe Pivotelement zu einem neuen Tableau

   • wenn Tableau optimal => fertig

   • sonst weitermachen