13.11.2022 Effekte und Arten von Gütern#
Einkommens und Substitutionseffekte#
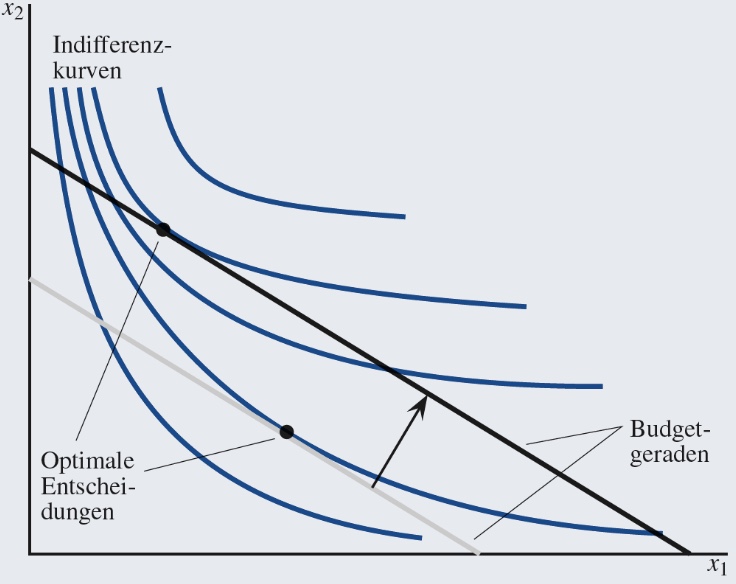
Effekte einer Preisänderung:
relative Wert des Einkommens = Fläche unter Geraden
Preisverhältnis = Steigung der Geraden
Hier: Preissteigerung \(x_1\)
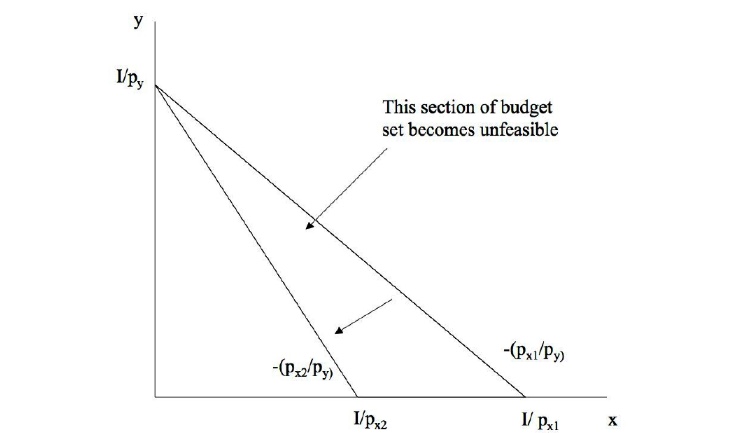
Unterteilung in:
Substitutionseffekt: die Nachfrageänderung nach einem Gut, die sich infolge einer Änderung der relativen Preise (d. h. des Preisverhältnisses) ergibt
Substitutionseffekt = immer negativ! (Preis steigt => Menge sinkt)
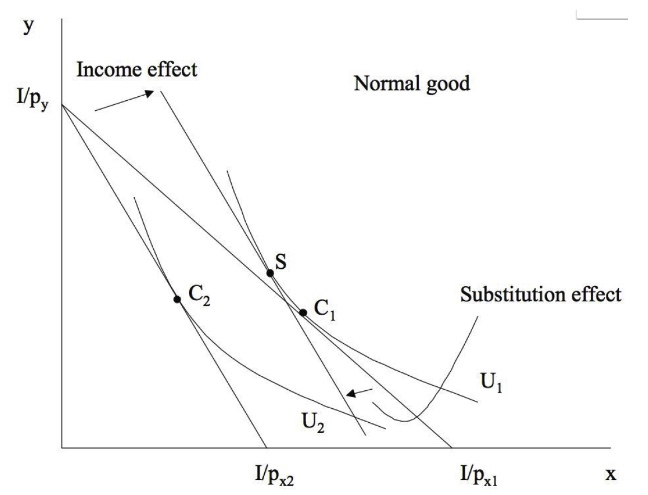
Einkommenseffekt: die Änderung der Nachfrage nach einem Gut, die sich infolge einer Änderung des (realen) Einkommens einstellt
kann positiv sein = normales Gut (weniger/mehr Einkommen -> weniger/mehr Nachfrage)
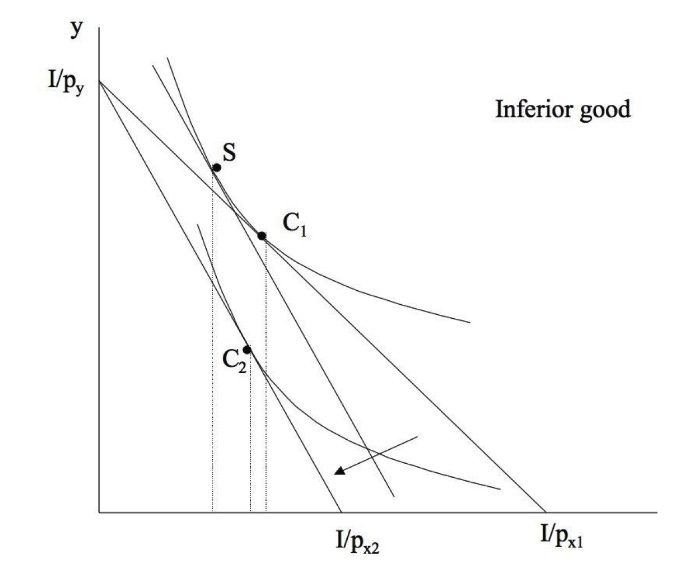
kann negativ sein = inferiore Güter (mehr Einkommen -> weniger Nachfrage)
Zerlegung der Effekte durch:
Hicks-Zerlegung: wenn wir Konsumenten für Einkommenseffekt kompensieren würden, wie hätte sich dann trotzdem sein Verhalten aufgrund von Preisverhältnis geändert
Slutsky-Zerlegung: Oder wir kompensieren, so dass Original Güterbündel erreichbar ist
Arten von Gütern#
Gut |
Effekte |
Grafik |
|---|---|---|
normales Gut: höherer Preis = niedrigere Nachfrage |
SE -> EE -> |
|
schwach inferiores Gut = mehr Einkommen = weniger Nachfrage |
SE -> <- EE |
|
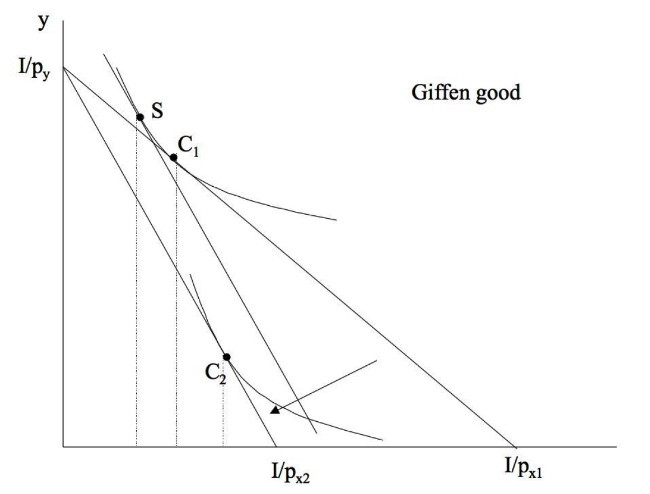
stark inferiores Gut (Giffen) = höherer Preis = höhere Nachfrage |
EE -> <-SE |
|
Kompensierte / unkompensierte Nachfrage#
Nachfragefunktionen: Änderung der nachgefragten menge bei Preisänderung
Marshallsche Nachfrage misst Gesamteffekt = unkompensiert
Hicksche Nachfrage bezieht sich nur auf andere Preise und Nutzeniveau = kompensiert
=> Hicksche misst Substitutionseffekt
Hicksche Nachfragefuntkion (\(h_x\)) bei Niveau U = Marshallsche Nachfrage \(d_x\) bei Einkommen für gleiches Nutzenniveau $\( h_x(p_x,p_y, \bar{U}) = d_x(p_x,p_y, \underbrace{E(p_x,p_y,\bar{U})}_I) \)$ also an Ausgangspunkt treffen sich beide, sonst verlaufen sie unterschiedlich! (abhängig von Güterart)
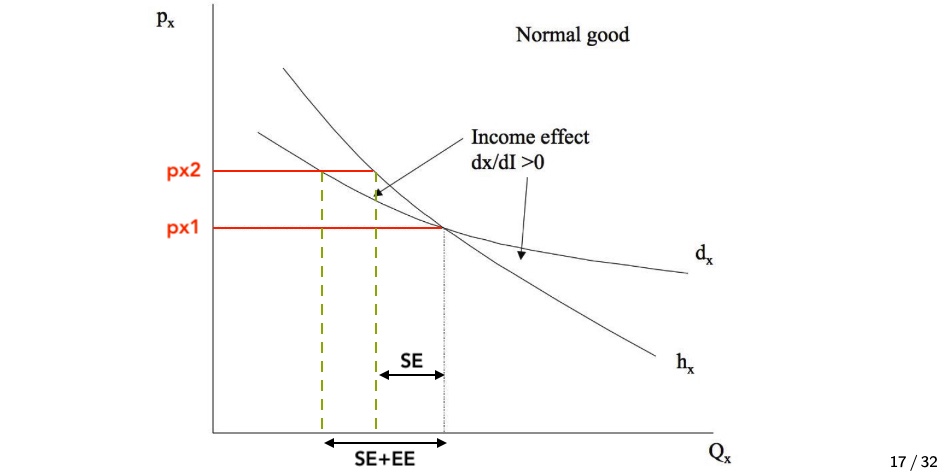
anhand der Verläufe lassen sich die Effekte extrahieren
Shephards Lemma und Slutsky Gleichung#
Stephards Lemma $\( \underbrace{\frac{\partial d_x}{\partial p_x}}_{1.} = \underbrace{\frac{\partial h_x}{\partial p_x}}_{2.} - \underbrace{\frac{\partial d_x}{\partial I_{}}}_{3.} \cdot \underbrace{\frac{\partial E}{\partial p_x}}_{4.} \)$
Änderung unkompensierte Nachfrage
Änderung der kompensierten Nachfrage
Änderung der Nachfrage bei kleiner Einkommensänderung
Optimal nachgefragte Menge = \(h_x\) = Shephards Lemma
was heißt das bitte?
bei ganz kleiner Preissteigerung = keine Reoptimierung der Güter = direkte Kompensation kann helfen
Beispiel: Wenn Sie jeden Tag 2 Kaffee in der Mensa kaufen und der Preis um 1 Cent steigt, brauchen Sie 2 Cent mehr, um das Nutzenniveau von vor der Preiserhöhung (U) halten zu können
Slutsky Gleichung: zeigt Zusammenhang zwischen beiden Nachfragefunktionen $\( \frac{\partial d_x}{\partial p_x} = \frac{\partial h_x}{\partial p_x} - \frac{\partial d_x}{\partial I }-x \)$ Arten der Güter werden sichtbar
Normales Gut: \(\frac{\partial d_x}{\partial p_x}<0\)
Inferiores Gut \(\frac{\partial d_x}{\partial I} < 0\)
schwach inferior, wenn dennoch \(\frac{\partial d_x}{\partial p_x} < 0\)
Giffen Gut, wenn \(\frac{\partial d_x}{\partial p_x}>0\)
Übung#
Aufgabe 1: Definitionen#
Hicksche Nachfrage:
nachgefragte Menge, gegeben Preise und Nutzenniveau
Unkompensiert, weil gegebens Nutzenniveau
Marshallsche Nachfrage:
nachgefragte Menge, gegeben Preise und Einkommen
Kompensiert, weil es Gesamteffekt einer Veränderung darstellt
Substitutionseffekt
Effekt, der durch Änderung der relativen Preisverhältnisse zustandekommt
Konsumentin wird bei Preisänderung quasi einkommensmäßig entschädigt
Einkommenseffekt:
Effekt, der zustandekommt durch Veränderung des Einkommensniveaus bei Preisänderung
Aufgabe 2: Effekte#
Nutzenfunktion: $\( U = x_1^{1/2} x_2^{1/2} \)$
bereits bekannt (für diese Nutzenfunktion):
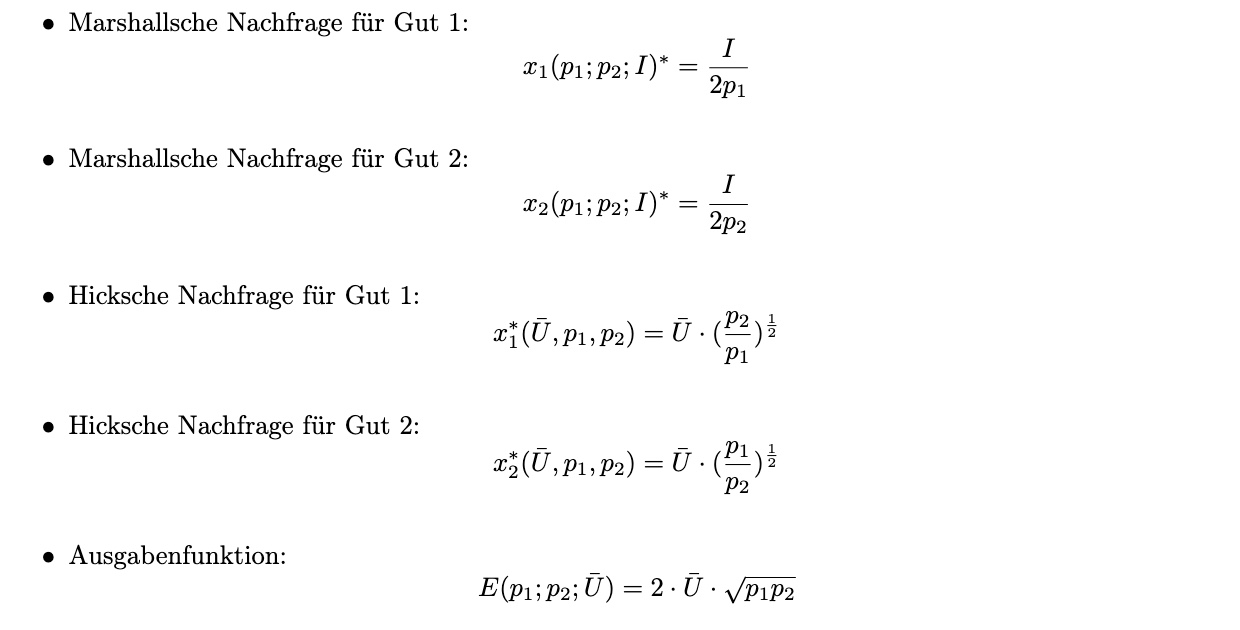
gegeben:
\(U = 100\)
\(p_1 = 1\)
\(p_2= 4\)
Rechnungen
IDK: \(U = 100=x_1^{1/2} x_2^{1/2} \to x_2 = \frac{10000}{x_2}\)
Einkommen: \(E(p_1,p_2,U)=2U\cdot \sqrt{p_1p_2} = 2U\cdot \sqrt{p_1p_2} = 400\)
Budgetgerade: \(400=1 * 0+ 4 x_2 = P_O(0;100)\)
Optimum \(x_1^* = \frac{I}{2p_1} = \frac{400}{2}=200\)
Optimum x2 aus Budgetgerade
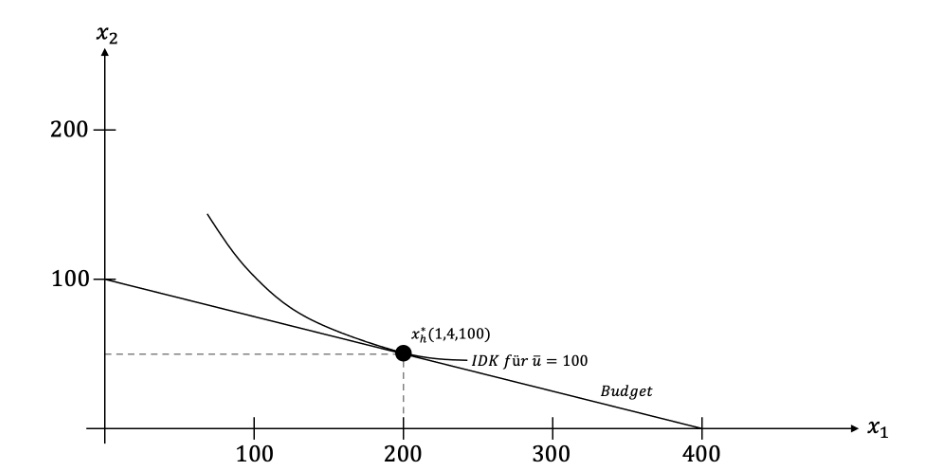
Jetzt: Preissteigerung \(p_1 = 4\)
welches Einkommen für gleichen Nutzen:
\(E(4,4,100) = 2 * 100*\sqrt{4*4}= 800\)
also doppeltes Einkommen
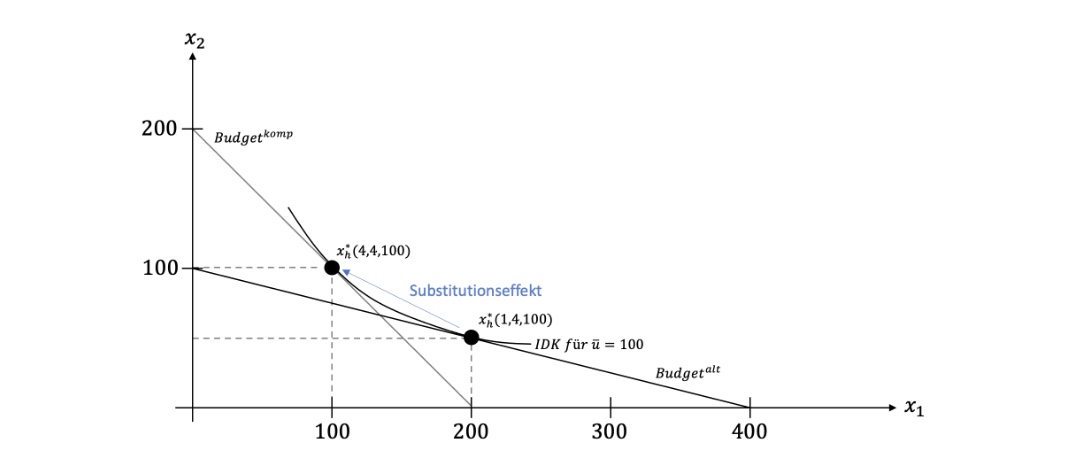
Substitutionseffekt mit Kompensation#
Preissteigerung \(p_1 = 4\)
Hicksche Nachfrage für Gut 2:
\(x_2^*(100,1,4) = 50\) (Ausgangssituation)
\(x_2^*(100, \bold{4}, 4) = 100\) (nach Preissteigerung)
\(\Delta x_2 = 100-50 = 50\)
Preisänderung bei kompensiertem Einkommen führt zu: 50 mehr \(x_2\) und weniger \(x_1\)
Substitutionsefekt ohne Kompensation#
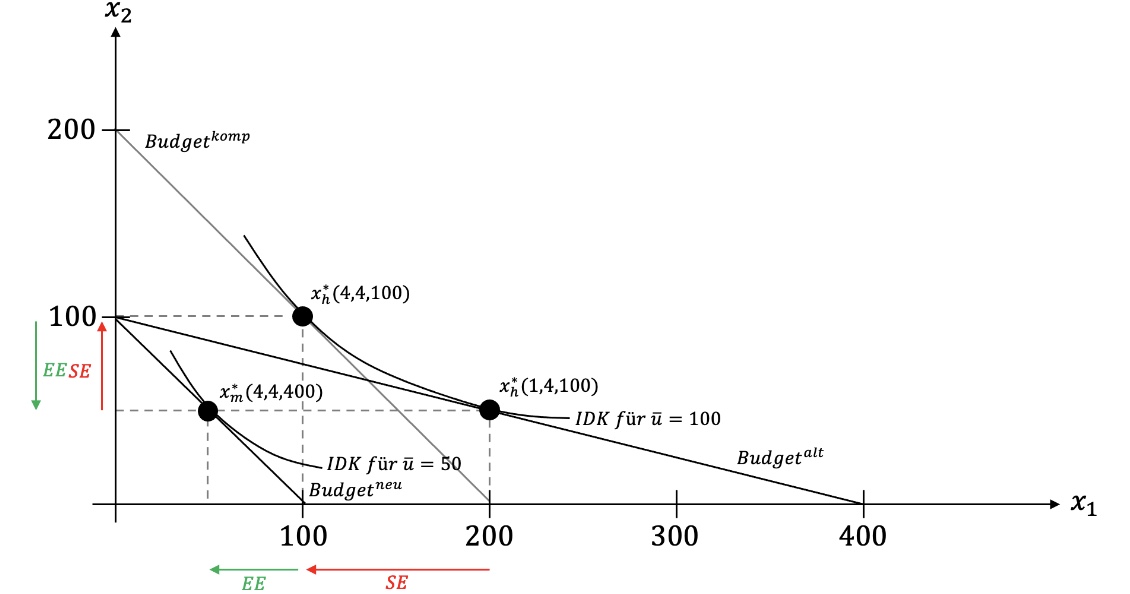
Preissteigerung \(p_1 = 4\)
mit Marshall für I=400 und p1=4
\(x_2 = (4,4,400)= \frac{I}{2p_2} = \frac{400}{8}=50\)(gleich wie Ausgangssituation)
\(\Delta x_2 = 50-50 = 0\)
\(x_1(4,4,400) = 50\) (nach Preisänderung)
also \(\Delta x_1 = 200-50 = 150\)
Durch die Preisänderung verschiebt sich nur die Menge am teurer gewordenen Gut, das andere bleibt gleich (für diese symmetrische Nachfragefunktion)
Aufgabe 3: Güterarten#
Normales Gut: Einkommensteigerung = mehr Nachfrage
Inferiores Gut: Einkommensteigerung = weniger Nachfrage
Gut 1 hier inferior :