17.11.2022 Erklärungen für langfristiges Wirtschaftswachstum#
Catch-Up Wachstum#
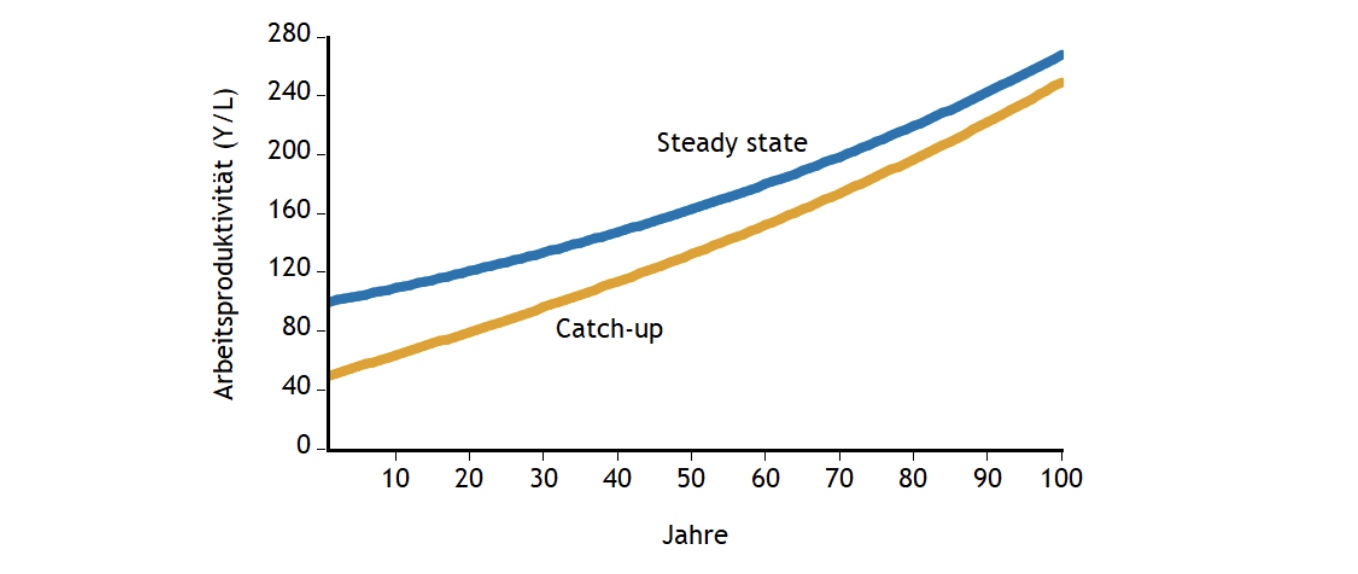
auholdendes Wachstum durch Bewegen auf Steady-State
Konvergenz der Arbetisproduktivität
je weiter vom Steady State entfernt => schnelleres Wachstum
Empirisch: 2% Lücke schließen pro Jahr (bei gleichen Bedingungen)
bsps. Nord/Süd USA, Ost/Westdeutschland, Süd/Norditalilien
Wachstumsclubs#
Annahme: es gibt 2 Arten von Ländern, eine folgt Solow (grün) andere nicht (blau)
Wachstum für ärmere Länder höher?
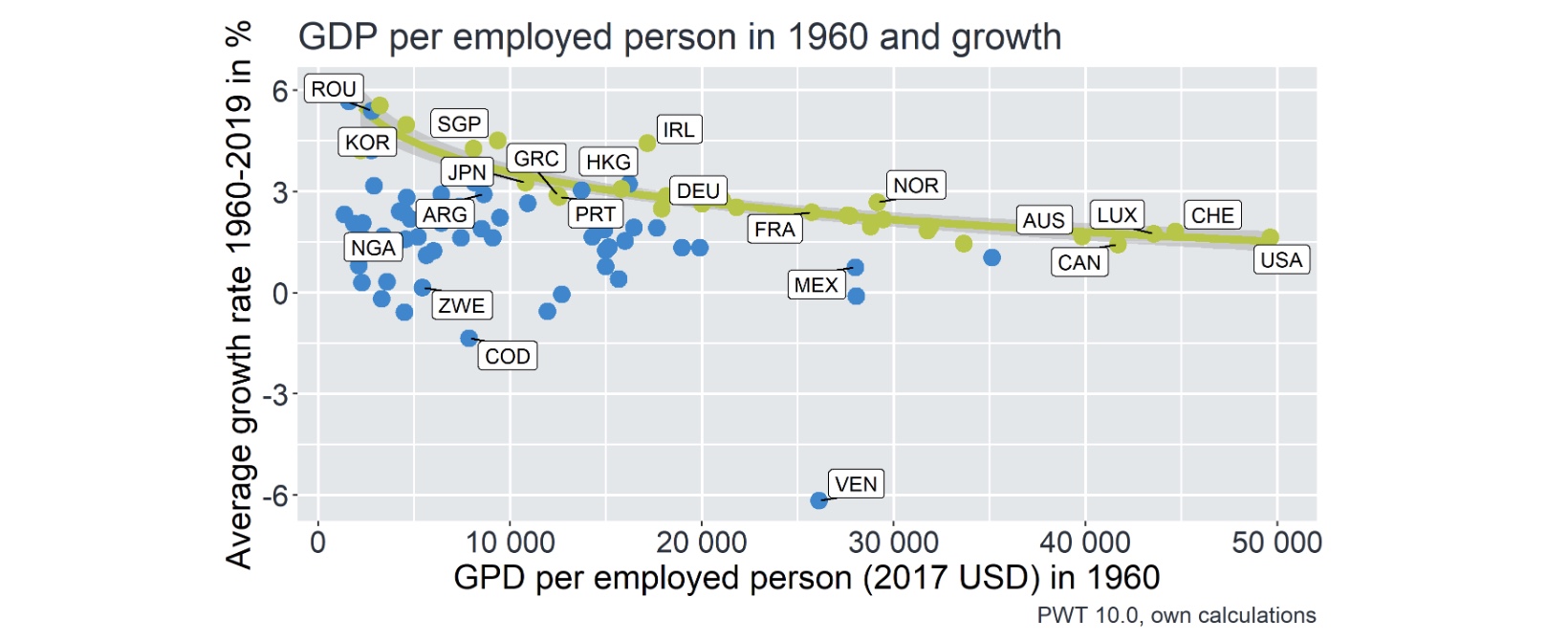
Bedingte Konvergenz#
Annahme: die Effizienz Z der Anwendung von Technologie ist unterschiedlich
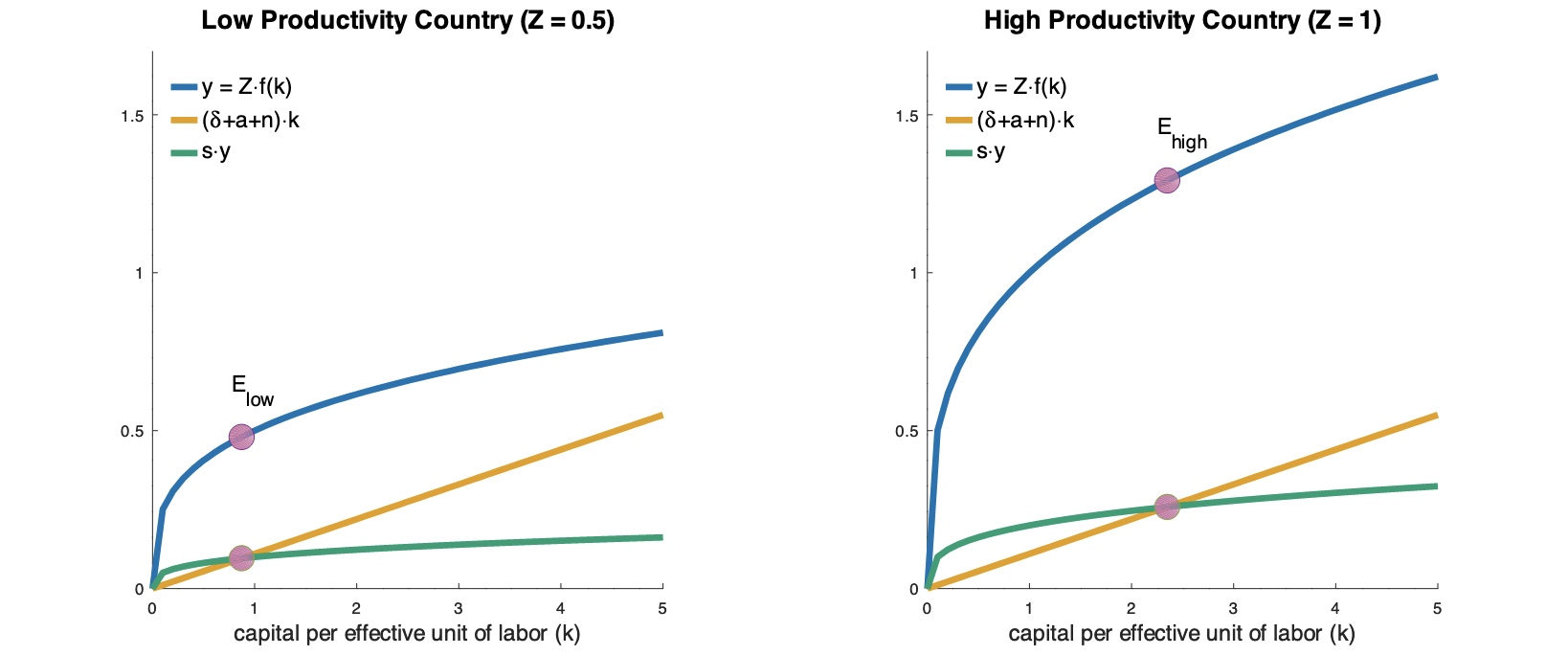
Erklärungen für Z:
Geographie
Kultur (aka Arbeitsethos)
Institutionen
Institutionen#
beispielsweise Wirtschaftssystem/ Rechtssicherheit …
Beispiel Ost / West:
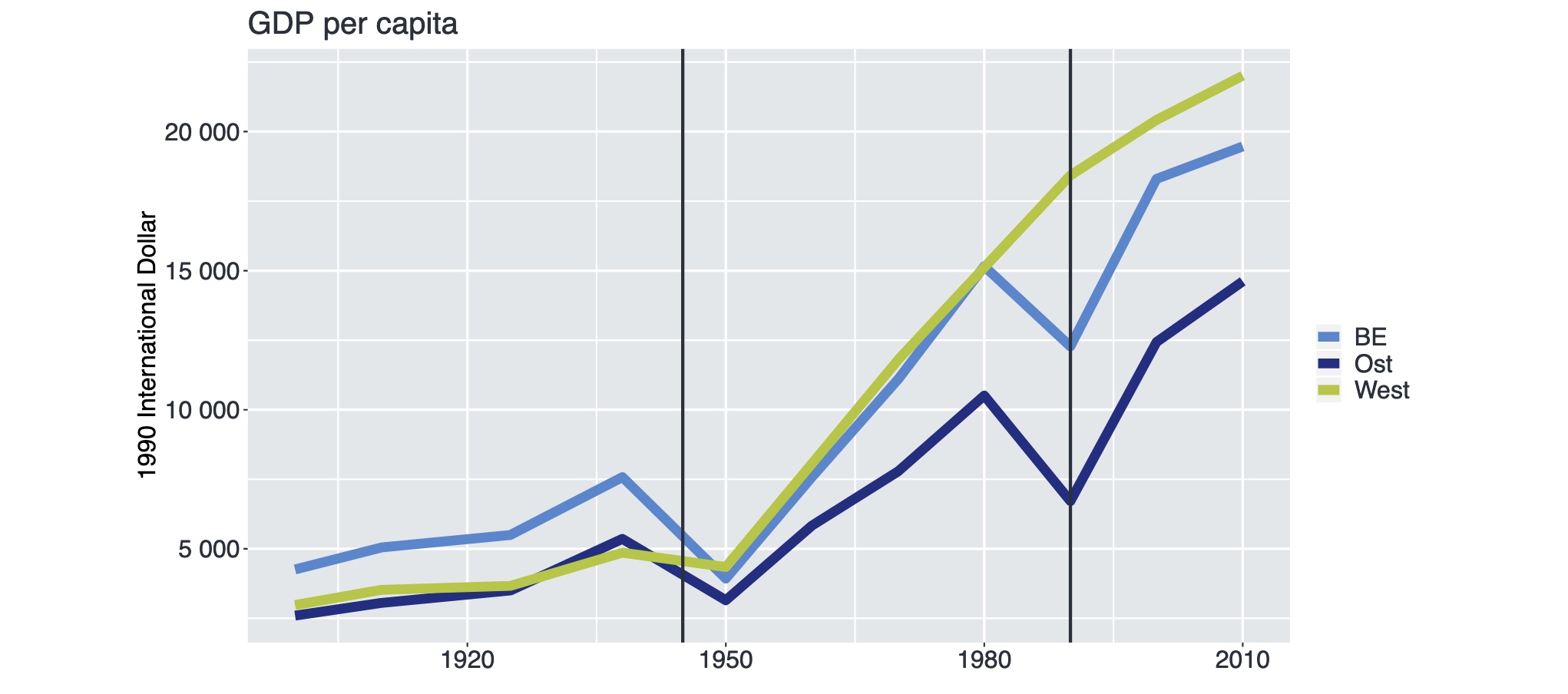
Soziale Normen
Eigentumsrechte
Menschenrechte
Humankapital
Bildung
Gesundheit
Forschung / Entwicklung
Öffentliche Infrastruktur
Verkehr
Kommuniaktion
Energie
Endogenes Wachstum nach Romer#
Solow Modell frage: Wie entsteht technologischer Fortschritt im System (endogen)?
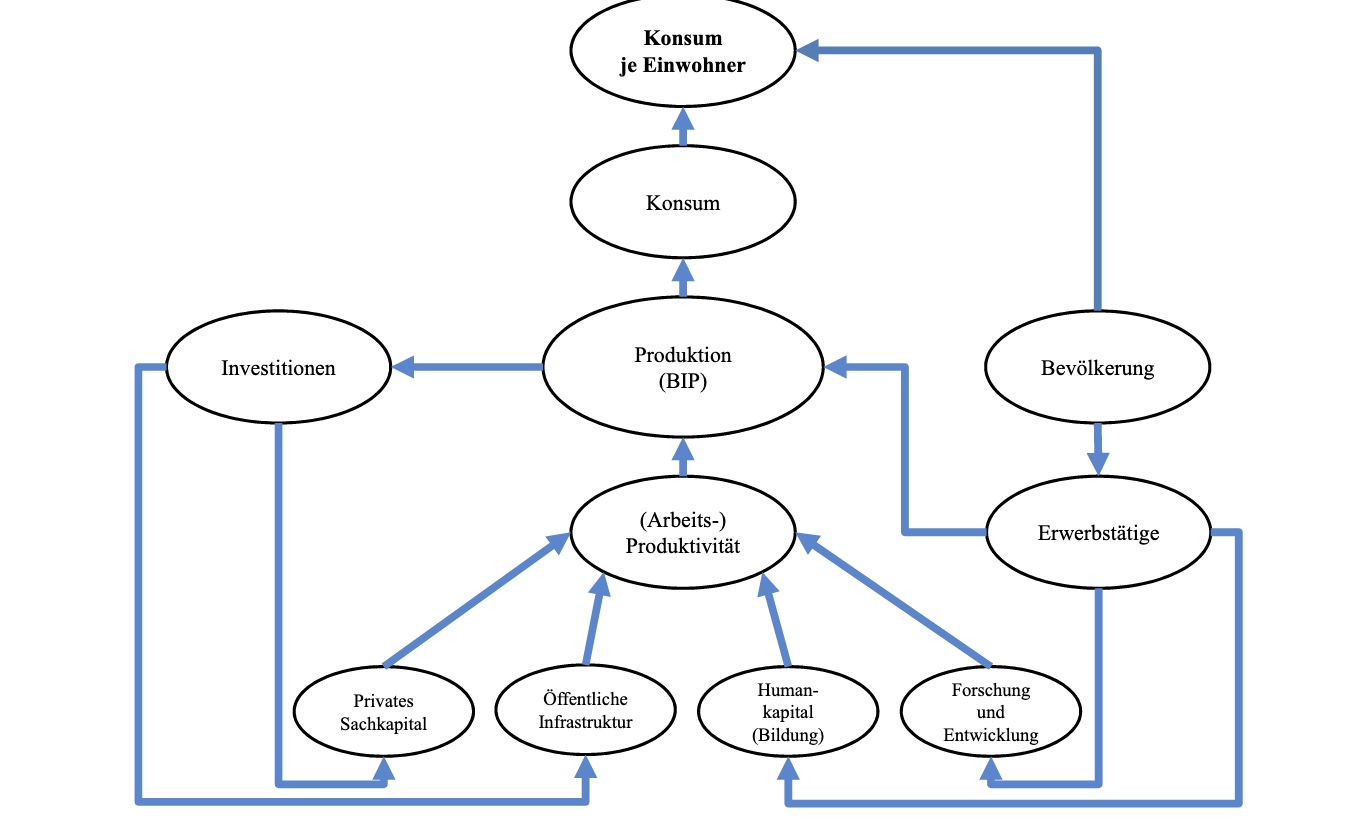
Romers Antwort:
Aufteilung Güterproduktion und Ideenproduktion (Forschung)
dann Forscher \(L_A\) und Arbeiter \(L_Y\)
Anteil der Forscher an Bevölkerung \(\gamma_A\)
sie können dann aber kein Anteil an Wachstum an sich haben
Produktivität der Ideenproduktion = u
Mathematisch#
Bevölkerungsaufteilung: $\( L = \underbrace{(1-\gamma_a)L}_{Arbeiter} + \underbrace{\gamma_a L}_{Forscher} \)\( Wachstum technologischer Fortschritt: \)\( \hat{A} = \frac{\gamma_a}{u}L \)$
Produktionsfunktion: $\( Y = A K^\alpha \big[(1-\gamma_a) L\big]^{1-\alpha} \)\( Wachstumsrate: \)\( \hat{y}_t = \frac{1}{1-\alpha} \frac{\gamma_A}{\mu} L \)$
Effekt einer Erhöhung des Anteils der Forscher#
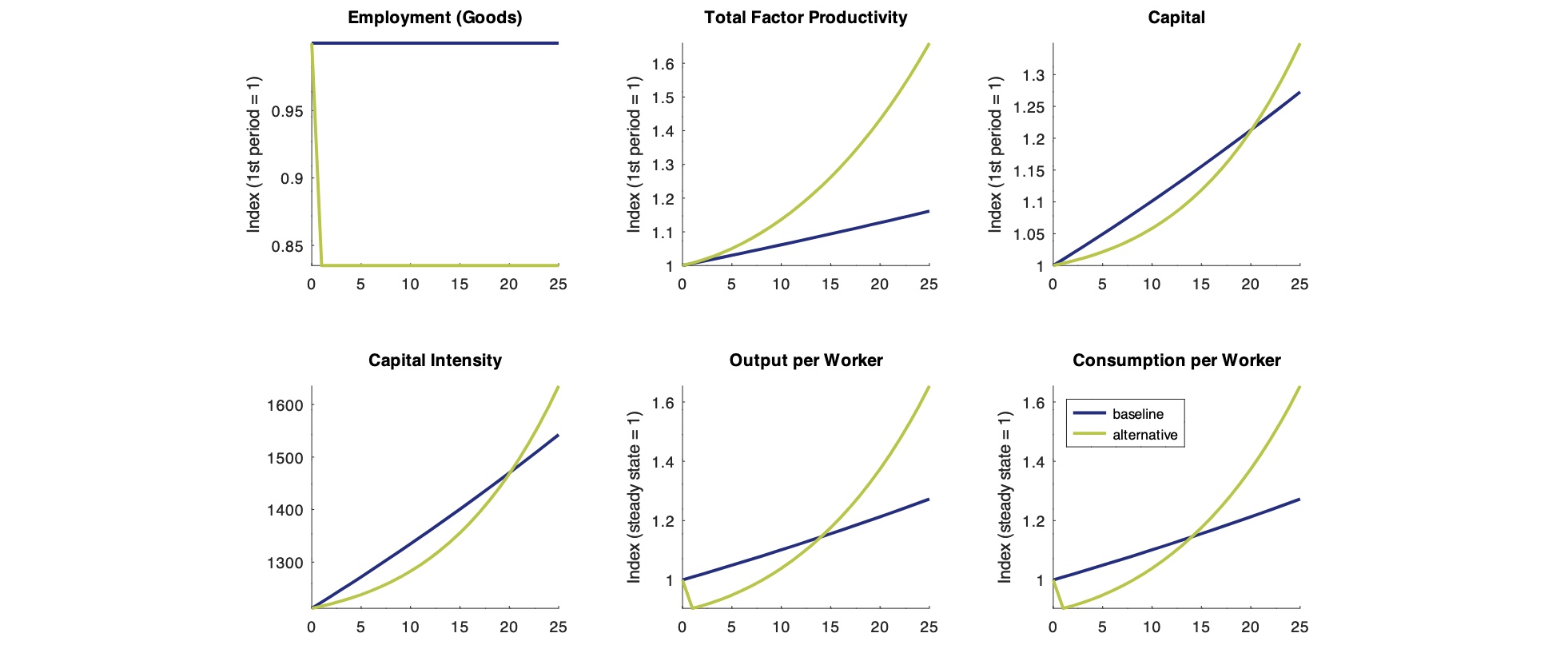
Implikationen#
individuelle Investitionen in F&E haben positiven externen Effekt
wird aber nicht in Berechnung einbezogen
Effekte wirken erst sehr langfristig
kurzfristige Politik ist whack
Humankapital nach Lucas#
Ein Anteil der Bevölkerung ist Lehrende und kann nicht schuften $\( Y = K^a H^b (AL)^{1-a-b} \)$ Humankapital wird angeschafft und entwertet (ähnlich zu echtem Kapital)
Übung#
Aufgabe 1#
Definitionen
Solow Residuum
das Technologielevel A im Solow-Modell
Teil des Wachstums, der nicht durch Kapitalakkumulation / Bevölkerungswachstum erklärt werden kann
„measure of our ignorance“
Konvergenzhypothese
Die Theorie, dass Länder, die nicht auf balanced growth path sind
schneller aufholen müssten zu Ländern im Steady State
da schnellere Kapitalakkumulation
bedinge Konvergenz
die anwendung der Technologie wird unterschiedlich effizient
durch die höhere Effizienz Z in reicheren Ländern kann nur bedingt aufgeholt werden
da Pfade unterschiedlich
Wachstum bei Solow
Kapitalakkumulation \(\Delta k\) (endogen)
Bevölkerungswachstum a (exogen)
technologischer Fortschritt g (exogen)
Berechnung des Residuums mit Totalem Differenzial $$ Y = A_t K_t^\alpha L_t^{1-\alpha} \newline \to TD:
\frac{\Delta Y}{y} = \alpha\frac{\Delta K}{K}+ \underbrace{\frac{\Delta A}{A}}_{SR}+ (1-\alpha)\frac{\Delta L}{L}
\newline \dot{Y} = \alpha k + a+(1-\alpha)n $\( Grenzprodukt des Kapitals = Outputelasitiziät \)\( \frac{\frac{dY}{Y}}{\frac{dK}{K}} = \frac{dY}{dK}\frac{K}{Y} = \alpha \)$ Alpha = Anteil des Kapitals an Einkommen
Aufgabe 2#
Produktionsfunktion $\( Y = AK^{0.4} L^{0.6} \)$ Situation 1: keine Forscher
Produktiosnfunktion unverändert
Wachstumsrate mit Wachstum der Bevölkerung und Wachstum der Technologie \(\dot{Y} = a+n\)
Situation 2: Annahme mit Forschenden , anteil \(\gamma_a\) an Bevölkerung
Produktionsfunktion: \(Y = AK^{0.6}((1-\gamma_a)L)^{0.4}\)
Wachstumsrate des Outputs:
Wie kann Technolgie entwickelt werden:
Innovationsksoten \(\mu\) sinken
Anteil \(\gamma_a\) steigt
L steigt (c.p mehr Forscher)