20.05.2022 Versicherung#
Risikofreude#
Entscheidungen von Akteuren sind risikobehaftet, Bereitschaft zu Risiko = individuell
Mögliche Wahrscheinlichkeitsverteilung einer Entscheidung \(W = [s_1,...,s_n \ ; \ \pi_1, ...,\pi_n]\)
mit Ergebnissen \((s_1,..,s_n)\) und Wahrscheinlichkeiten \((\pi_1,...,\pi_n)\)
Beispiel Lotterie#
100€ Ausgangsvermögen
5€ Losticket,
50% Gewinnchance, 10€ Gewinn
\(W = [95,105; 0.5,0.5]\)
Erwartungswert: \(105*0.5 + 95*0.5 = 100\)
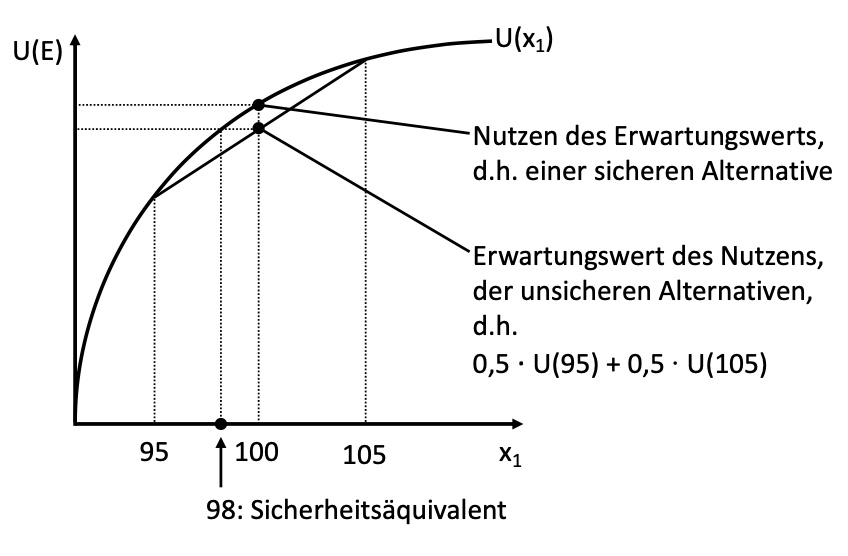
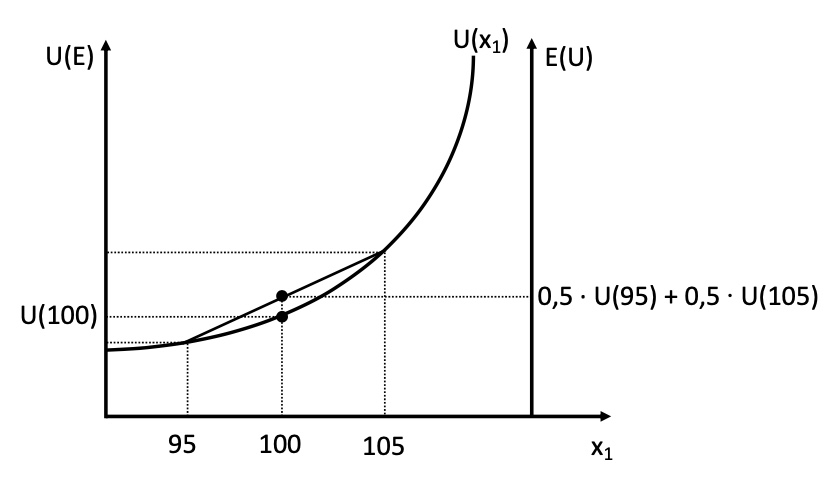
Entscheidung mithilfe von Neumann-Morgenstern-Nutzenfunktion des Erwartungswerts U(s) $\( U(s) =& U(s_1) * \pi_1 + U(s_2) * \pi_2 + ... + U(s_n) * \pi_n \\ U(s) =& 0.5 * U(95) + 0.5 * U(105) \)$ Verhalten dann abhängig von persönlicher Nutzenkurve des Loskäufers
Käufer 1 (risikoavers) |
Käufer 2 (risikofreudig) |
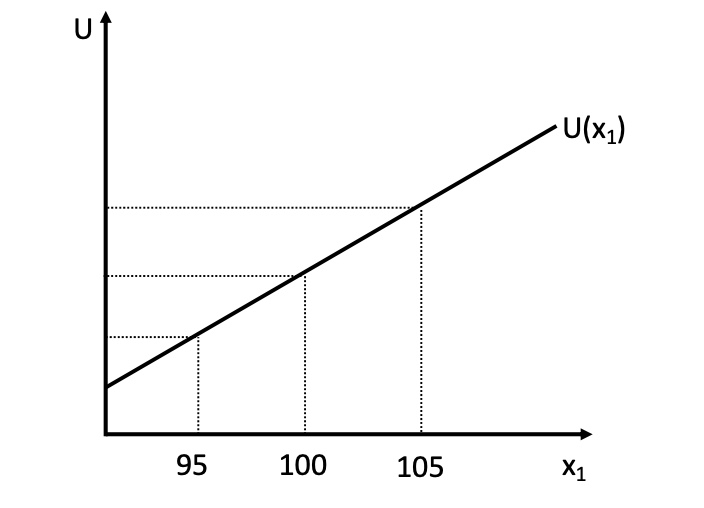
Käufer 3 (risikoneutral) |
|---|---|---|
|
|
|
strikt konkav |
strikt konvex |
Strikt geradlinig |
\(U(100) > 0.5 * U(95) + 0.5 * U(105)\) |
\(U(100) < 0.5 * U(95) + 0.5 * U(105)\) |
\(U(100) = 0.5 * U(95) + 0.5 * U(105)\) |
Risikoaverser Käufer ist bereit, Versicherung gegen Risiko anzunehmen
Prämie in Höhe des Sicherheitsäquivalentes
wenn er gezwungen wäre zu spielen!
mögliche Fälle
Outcomes |
keinen Schaden |
Schaden |
|---|---|---|
ohne Vers. |
\(y^*\) |
\(y^* -L\) |
mit Vers. |
\(y^*- (p*q)\) |
\(y^* - L+q - (p*q)\) |
y* = yield
L = loss
p = Versicherungsprämie
q = Versicherungssumme
Nachfrage nach Versicherungen#
Fälle g = good und b = bad
Abszisse = good Outcome
Ordinate = bad Outcome
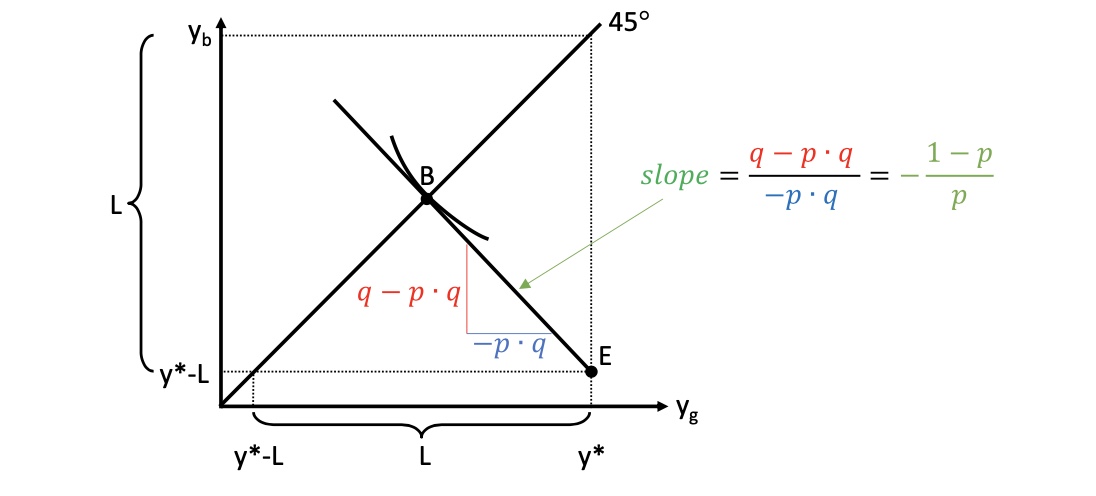
\(y_b\) = Einkommen im Schadensfall, das wir erhöhen wollen
\(y_g\) = Einkommen ohne Schadensfall
45° Linie = gleichmäßige Verteilung zwischen Eintreten beider Fälle
Haushalt ist dann indifferent zwischen beiden Fällen: \(MU_{y_b}=MU_{y_g}\)
Wichtig: Raum unterhalb der Achse, da nur dann positiver Fall
Ausgangsituation E ohne Versicherung
im guten Fall: \(y^*\)
im schlechten Fall: \(y^* - L\)
Punkt B: mit Versicherung
wir geben \(y_g\) auf, um bei \(y_b\) hochzuwandern
Punkt B = indifferent zwischen Eintreten beider Fälle
im guten und schlechten Fall zwischen \(y^*\) und \(y^* - L\)
Substitutionskönnen#
Marginal Rate of Transformation: \(\frac{1-p}{p} = MRT\)
Substitutionskönnen zwischen Einkomen im guten / schlechten Fall
durch aufgeben von 1€ -> im Schadensfall \(\frac{1-p}{p}\) Euro mehr
Substitutionswollen#
Schadenswahrscheinlichkeit = \(\pi\)
höhere Schadenswahrscheinlichkeit => höhere Bereitschaft für Verzicht
Gleichgewicht#
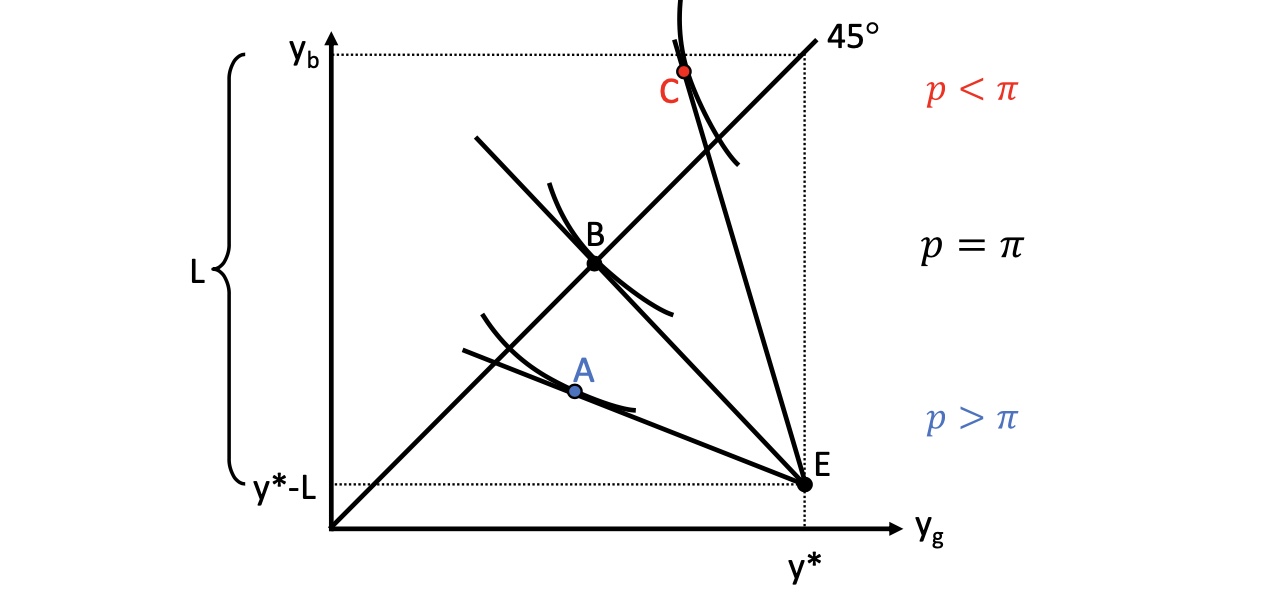
in optimalen Punkt: MRS = MRT mit festem \(\pi\) ! $\( \frac{1-\pi}{\pi} * \frac{MU_{y_g}}{MU_{y_g}} = \frac{1-p}{p} \)$ Verhalten bei verschiedenen Prämiensätzen:
bei fairer Prämie: Haushalt wählt Vollversicherung
\(p = \pi\) ist aktuarisch fair
bei unfairer Prämie \(p > \pi\): Haushalt wählt Unterversicherung, Punkt A
Bei gönnerhafter \(p < \pi\): Haushalt überversichert, Punkt C
Probleme asymmetrischer Information#
Adverse Selection#
Problem: ungenaue Information der Versicherung über exakte Schadenswahrscheinlichkeit
Informationsasymmetrie vor Abschluss
Beispiel: zwei Haushalte mit unterschiedlichen Risiken \(\pi_1 >\pi_2\)
Haushalt mit hohem Risiko verschleiert sein wahres Risiko
Versicherung schützt sich, indem es hohe Risikoprämien verlangt
oder nur noch Teilversicherungen anbietet
= adverse Selection = negativauslese = risikolose Haushalte werden verdrängt
Moral Hazard#
Problem für Versicherer nach Abschluss:
Haushalt lässt \(\pi\) ansteigen
oder vergrößert L
Informationasymmetrie nach Abschluss
Marktversagen#
Autoverkauf im Gebrauchtmarkt: Risiko eines schlechten Autos
große Unsicherheit => niedrigere Nachfrage => Marktineffizienz
Lösung: Verkäufer gibt Garantieerklärung
Übung#
Aufgabe 1#
Ausgangsituation: I
Einkommen = 100
möglicher Verlust = 75
mit Versicherung: E
p = 0.5
q = 60
P = p*q = 30
Graphik: 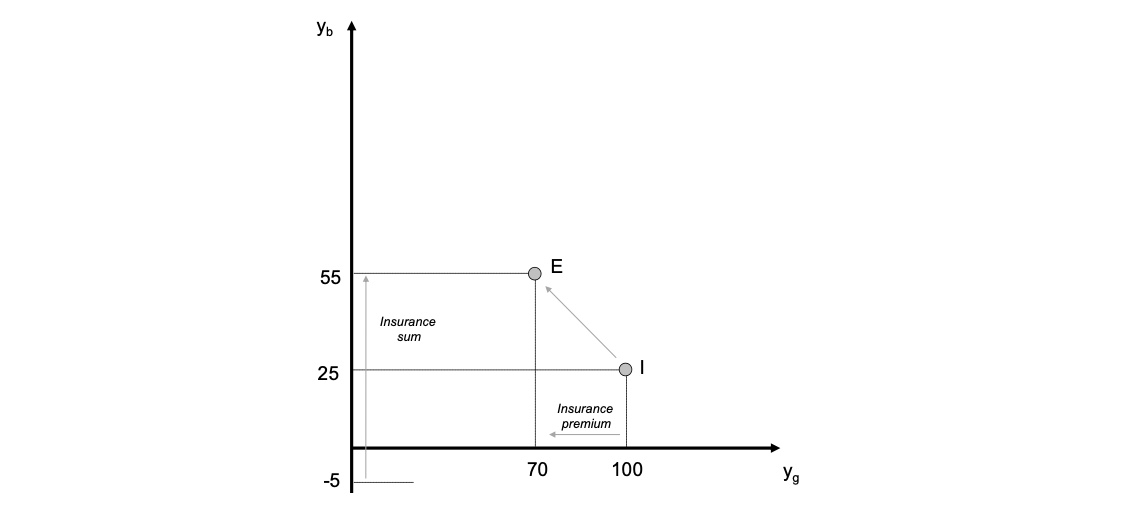
Aufgabe 2: Erwarteter Nutzen#
Nutzenfunktion des Haushalts: \(U = y^{0.5}\)
Schadenswahrscheinlichkeit: \(\pi = 0.4\)
Ausgangsituation:
Nutzen im guten Fall = \(100^{0.5} = 10\)
Nutzen im schlechten Fall = \(25^{0.5} = 5\)
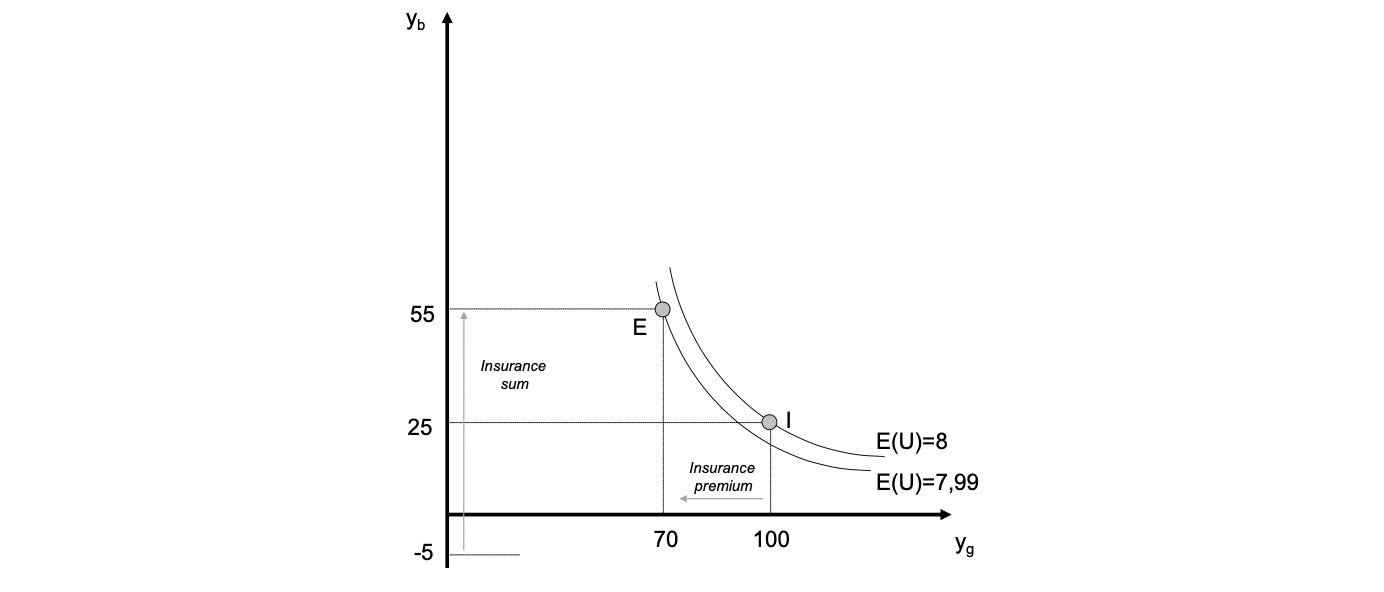
Erwarteter Nutzen: \(E(U)=0.4 * 5+ 0.6 * 10 = 8\)
Gleichung der Indifferenzkurve: $\( 8 =0.4 * y_b^{0.5}+ 0.6 * y_g^{0.5} \\ 8 - 0.6 * y_g^{0.5} = 0.4 * y_b^{0.5} \\ y_b^{0.5} = 20 - 1.5 y_g^{0.5} \\ y_b = \big[20-1.5y_g^{0.5} \big]^2 \)$ mit Versicherung:
\(E(U) = 0.4 * 55+ 0.6 * 70 = 7.99\)
weniger als ohne Versicherung
Aufgabe 3: Budgetgerade#
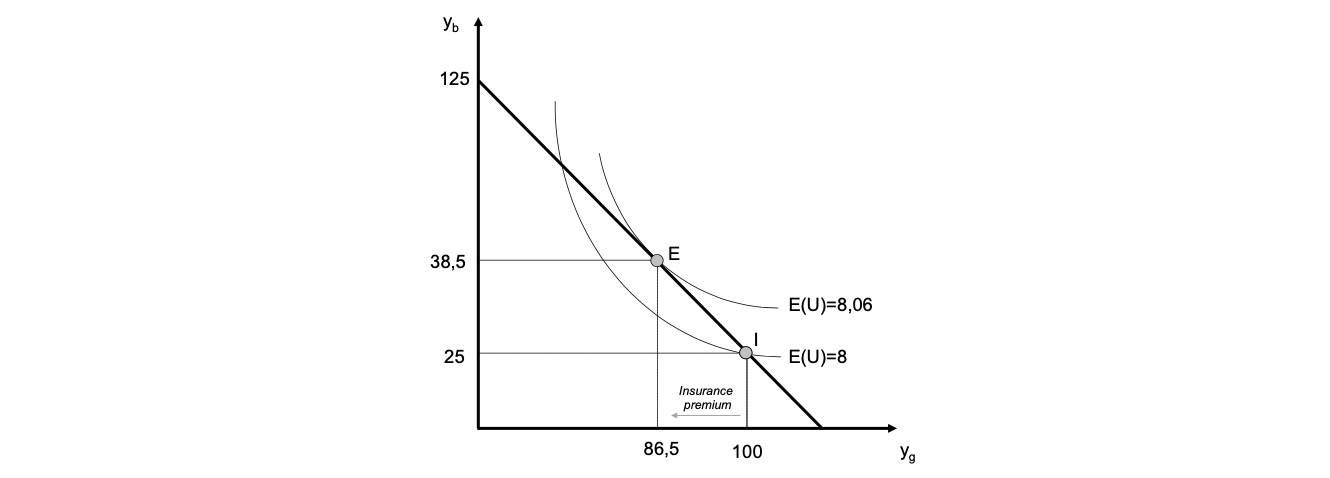
Bestimmung bei Prämie = 0.5 $\( \begin{aligned} MRT &= - \frac{1-p}{p} = -\frac{0.5}{0.5} = -1 \\ SPO &= \frac{y^*}{p}-L = \frac{100}{0.5}-75 = 125\\ y_b &= MRT \cdot y_g + SPO \\ y_b &= -1 \cdot y_g + 125 \\ \end{aligned} \)\( Gleichung: \)y_b = -1\cdot y_g+ 125$ (anhand des Ausgangspunktes bestimmt)
Aufgabe 4: Haushaltsgleichgewicht#
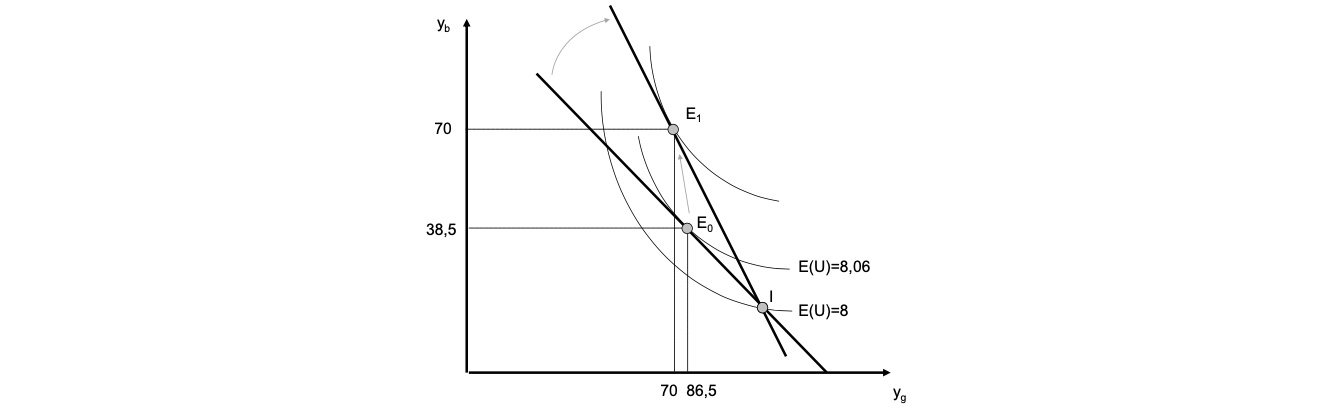
Maximierungsbedingung $\( \underset{y_g,y_g}{max E(U)} = \underset{y_g,y_g}{max}(0.4y_b^{0.5} + 0.6y_g^{0.5}) \\ s.t. \; y_b = -y_g+125 \)\( Langrange Funktion \)\( \begin{aligned} LF = 0.4y_b^{0.5} &+ 0.6y_g^{0.5} + \lambda [y_b+y_g-125] \\ \\ 1)\ \frac{\partial L}{\partial y_b} &= 0.6*0.5y_b^{-0.5}+ \lambda = 0 \\ 2)\ \frac{\partial L}{\partial y_g} &= 0.4*0.5y_g^{-0.5}+ \lambda = 0 \\ 3)\ \frac{\partial L}{\partial \lambda} &= y_b+y_g-125 = 0 \end{aligned} \)\( Gleichsetzen von 1) und 2) \)\( -0.3 y_g^{-0.5} = -0.2y_b^{-0.5} \\ y_g^{-0.5} = \frac{2}{3}y_b^{-0.5} \\ y_g = \frac{9}{4}y_b \)\( Einsetzen in 3) \)\( y_b + \frac{9}{4}y_b - 125 = 0 \\ \frac{13}{4}y_b = 125 \\ y_b^* = \frac{4*125}{13} = 38.5 \)\( Einsetzen in erstes Ergebnis \)\( y_g^* = \frac{9}{4}y_b \implies \frac{9}{4} \cdot 38.5 = 86.5 \)$ Optimum:
optimales Einkommen im Guten Fall = 86.5 €
Prämie = 100-86.5 = 13.5€
\(P = q\cdot p \to 13.5/0.5 = 27€ = q\)
Erwarteter Nutzen der Versicherung dann $\( E(U) = 0.4*y_b^{0.5} + 0.6*y_g^{0.5} = 0.4*38.5^{0.5} + 0.6*86.5^{0.5} = 8.06 > 8 \)$ der Nutzen dank der Versicherung ist größer als in der Ausgangsituation:
Gewinn der Versicherung: $\( G = E - K = p*q - \pi *q \\ 0.5*27 - 0.4* 27 = 2.7 \)$ Versicherung und Konsument sind bessergestellt; trotz aktuarisch unfairer Prämie!
Aufgabe 5: langfristiges Gleichgewicht#
langfristig wird \(p=\pi\) und Prämie aktuarisch fair
der Haushalt gleicht Einkommen in beiden Fällen exakt an
und wählt dann Vollversicherung (75€ abgesichert)
Graphisch: