26.01.2023 strategische Interaktion#
Standardspieltheorie#
Bedeutend, nicht nur in Ökonomik
Standard Theorie aber nicht alles erklärbar
Annahmen:
nutzenmaximierend (keine soziale Präferenz)
Rational (keine Beschränkungen der Rationalität)
=> Spieltheorie der Verhaltensökonomik integriert diese
Soziale Präferenzen#
Erweiterung der Neoklassik um Neid, altriusmus, Fairness
Erweiterung der Nutzenfunktion
um soziale Komponente
Präferenz zur Ausuahlung dritter (ob positiv oder negativ) = soziale Präferenz
Beispiele für Nutzenfunktion mit sozialer Komponente
Altruismus: \(u(x,y) = x + y\)
Neid: \(u(x,y) = x - y\)
Fairness nach Rawl:s \(u(x,y) = \min(x,y)\)
Ungleichheitsaversion: \(u(x,y) = - |x-y|\)
…
Empirisch bewiesen in folgenden Spielen:
Ultimatum Spiel#
erster Spieler (proposer) mit Anfangssaustattung (bspw. 10$)
kann zweitem Spieler (responder) Angebot mit beliebigem Anteil stellen
lehnt zweiter ab, beide gehen leer aus; (Reject)
nimmt an, wird dies realisiert (Accept)
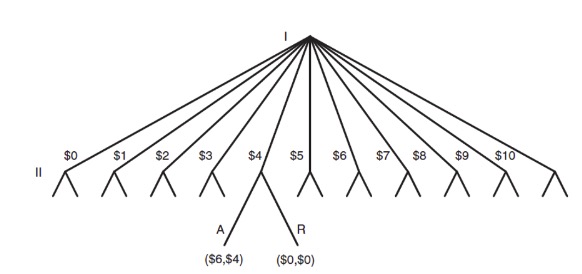
teilspielperfektes Gleichgewicht:
Spieler 1 wird nur wenig anbieten, aber über 0
zweiter Spieler nimmt rational immer an
Realität:
die meisten Angebote zwischen 40-50%
werden meist angenommen
Angebote unter 20% werden nur in der Hälfte der Spiele angenommen
=> Gerechtigkeitssinn spielt eine Rolle
Beispiel: zwei Utilitaristen mit \(U(x,y) = \sqrt{x}+\sqrt{y}\)
Spieler 2 würde immer annehmen
Spieler 1 würde maximieren => (5, 5)
Diktator-Spiel#
wie Ultimatum, nur mit passivem zweitem Spiel
der zweite muss hinnehmen, was er kriegt
Rational würde der Diktator nichts abgegeben (0%)
Realität:
Angebote zwischen 10-30%
kennt man die andere Person, mehr
unterschiedliche Nutzenfunktion erlauben unterschiedliche Ergebnisse
bspw. Gefangenendilemma mit Utilitaristischen Nutenfunktion
Absichten, Reziprozität und Vertrauen#
nicht alle Erkenntnisse lassen sich einfach mit sozialen Präferenzen erklären
=> aber nicht immer schön in Nutzenfunktionen einzubauen
Vertrauensspiel#
Spieler 1 und 2 jeweils Anfangssaustattung: \((A_1,A_2)\)
Sender (Spieler1) kann Betrag x abgeben, wird multipliziert mit a
Empfänger kann zurückgeben
Auszahlungen:
Sender: \(A_1 -x+y\)
Empfänger: \(A_2+ax-y\)
Rationales Ergebnis: keine Transfers zwischen Parteien
Empirie:
Sender schicken Hälfte der Ausstattung
Empfänger schickt ungefähr das zurück
Erklärung:
Sender vertraut auf Empfänger
Empfänger reagiert reziprok und sendet zurück
Public-Goods-Game#
Spiel mit mehreren Spielern
jeder mit Anfangsausstattung
jeder Spieler kann Betrag investieren
Summe der Investitionen mit Faktor multipliziert
Auszahlung aber ausgeteilt auf alle
Rationale Spieler würden niemals Geld hinzugeben
Empirie: viele geben einen Anteil, insbesondere bei Gruppenidentifikation
Beauty Contest#
Alle spieler nennen Zahl zw. 1 und 100
Spieler mit Zahl am nächsten an 7/10 des Durchschnitts gewinnt
Ansätze:
niedrigere Zahl ist sinnvoller
da andere aber gleiche Überlegung
alle immer niedriger
Empirie:
viele Spieler nicht rational
und dann keine Strategie mehr sinnvoll
individuelle Nash-GG oft nicht einstellen
bspw. Aktienblasen relevant
solange andere kaufen, ist es sinnvoll weiterzumachen
nur immer einen Schritt voraus sein