21.05.2022 Monopol und Oligopol#
bisher betrachteter Markt: 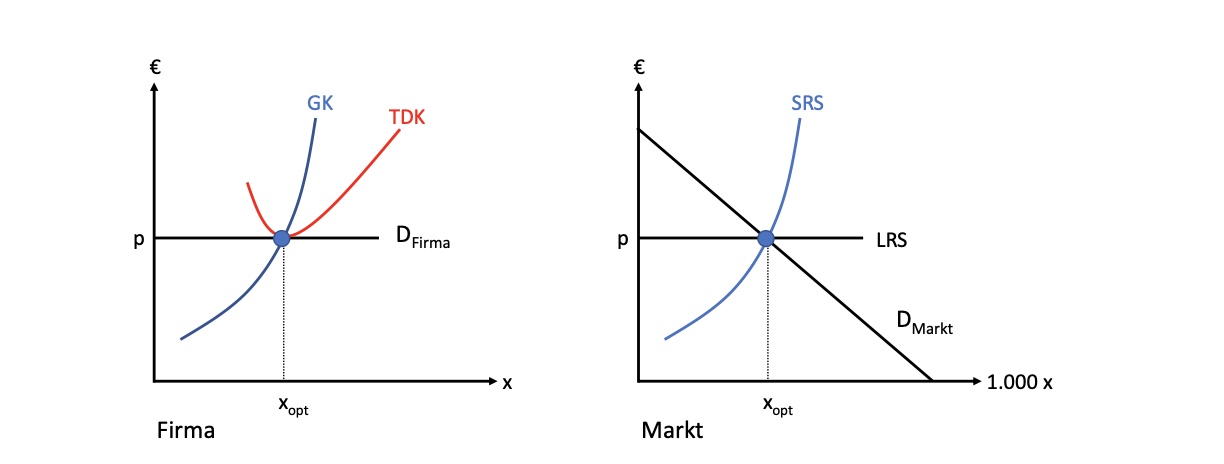
Polypol: Wettbewerbsmarkt mit vielen Teilnehmern ohne Preissetzungsfähigkeit
Entscheidungsvariable = Menge zu gegebenem Preis = Grenzkosten
Monopol#
Jetzt: Monopol!
Angebot basiert nicht mehr auf Grenzkosten
sondern Grenzerlöse GE
Preis ist für Monopolisten nicht fest
Mengenfixierung#
Gedanken des Monopolisten bei Verkauf einer Einheit:
Verkauf = zusätzlicher Erlös
Einheit produzieren = Grenzkosten
zusätzliche Einheit senkt Preis aller infra-marginalen Einheiten, die davor zu höherem Preis verkaufbar waren !
Monopolgewinn: \(Gewinn = Umsatz - Kosten = p(X) * X - K(X)\)
Preis ist abhängig von Menge!
deswegen Nachfrage = Preis-Absatz-Kurve PAF
wie immer: ableiten nach X und nullsetzen $\( \frac{\partial G}{\partial X} = \underbrace{\frac{\partial p}{\partial X} * X}_{T_1} + \underbrace{p* \frac{\partial X}{\partial X}}_{T_2} - \underbrace{\frac{\partial K}{\partial X} }_{T_3} = 0 \text{ mit } \frac{\partial X}{\partial X} = 1 \\ \to T_1 + T_2 - T_3 = 0 \)$
\(T_1\) = infra-marginale Umsatzwirkung einer Produktionsmengenerhöhung = negativ
\(T_2\) = marginale Umsatzwirkung = positiv
\(T_3\) = Grenzkosten
Gewinnregel für Monopol: \(T_2 = -T_1+ T_3\)
Effekt einer Mengenerhöhung um 1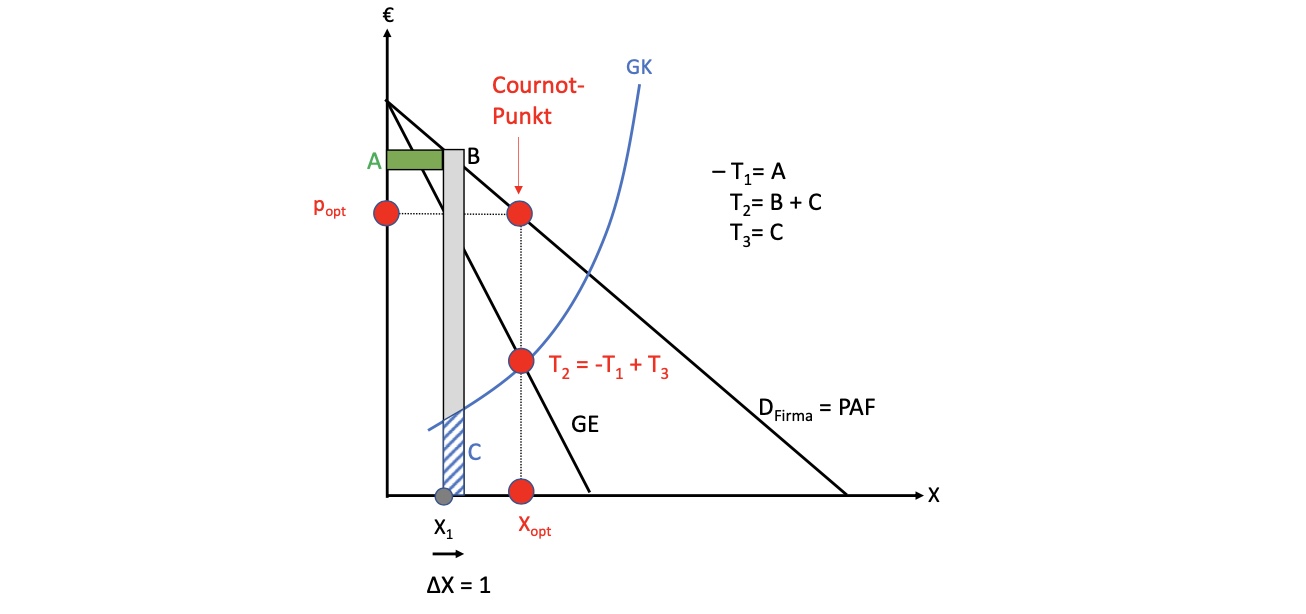
senkt Preis von allen Einheiten = A
erhöht Grenzkosten = C
erweitert Erlöse = B + C
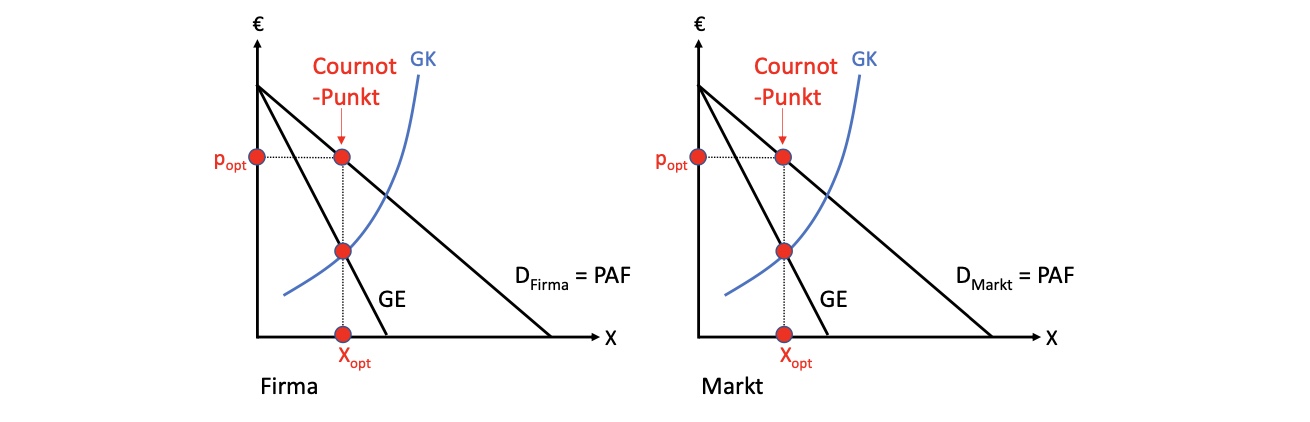
optimale Menge: GK = GE (Grenzerlös = Grenzkosten)
Merke: erst Menge bei Schnittpunkt ablesen, dann auf PAF projizieren für Preis
Preisfixierung#
Alternativ: Monopol kann einfach Preis fixieren und Nachfrager Menge entscheiden lassen
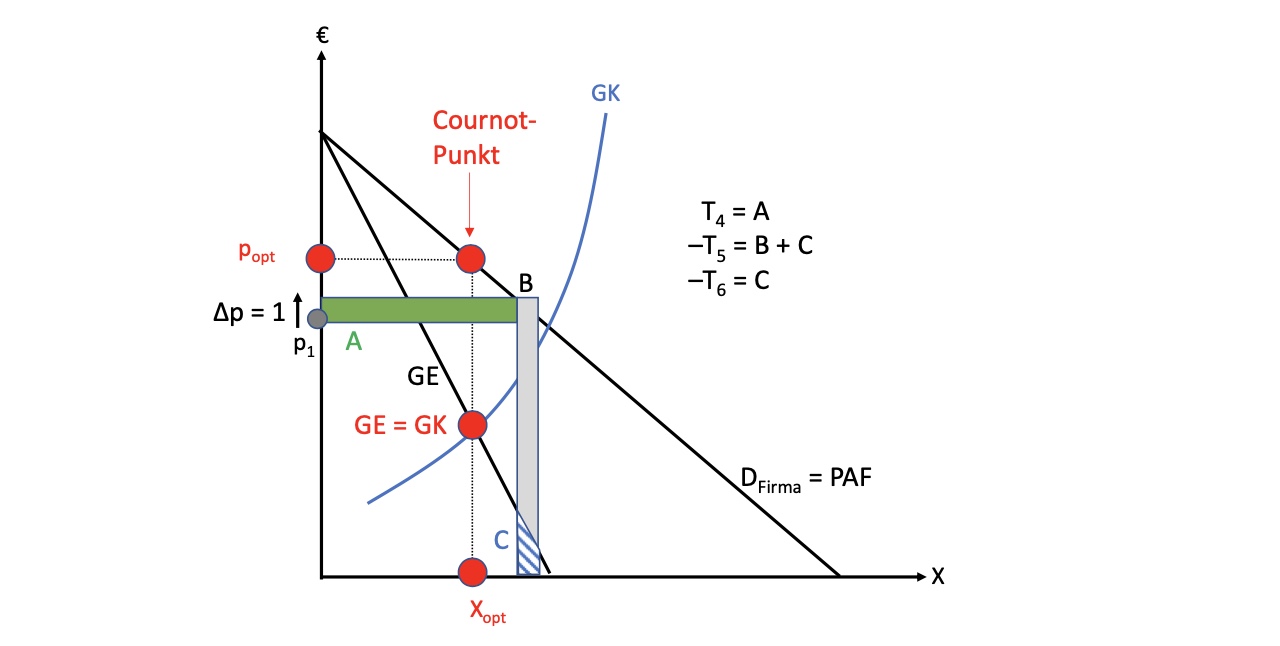
Modell: \(G [X(p)] = p*X(p)- K[X(p)]\) mit Entscheidungsvariable p $\( \frac{\partial G}{\partial p} = \overbrace{\frac{\partial p}{\partial p} * X}^{T_4} + \overbrace{p* \frac{\partial X}{\partial p}}^{T_5} - \overbrace{\frac{\partial K}{\partial X} * \frac{\partial X}{\partial p}}^{T_6} = 0 \text{ mit } \frac{\partial p}{\partial p} = 1 \\ \to T_4 + T_5 - T_6 = 0 \)$
\(T_4\) = Umsatzerhöhung einer Preiserhöhung
\(T_5\) = Umsatzverlust uafgrund gestiegenem Preise
\(T_6\) = Grenzkosten
Amoroso-Robinson-Formel#
Aussagen:
wenn Elastizität unendlich; Monopolpreis = Grenzkosten = Polypolbedingung
je niedriger Elastizität => höhere Monopolpreisaufschlag
Monopolpreis über Grenzkosten, wenn Elastizität nahe 1
Monopolisten wollen aber niemals in unelastischen Bereich
Wohlfahrtseffekte#
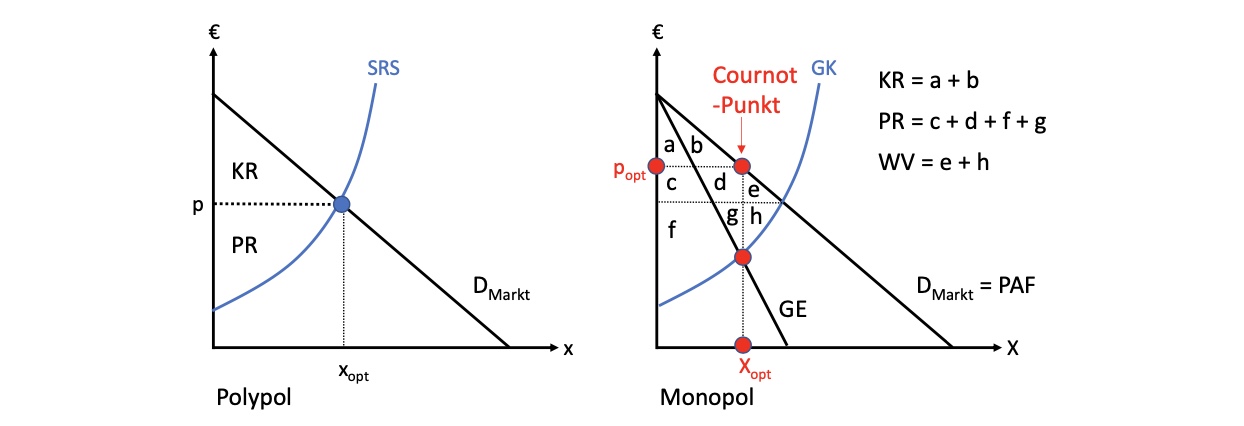
Effekte eines Monopols auf Konsumenten
verlieren e = Wohlfahrtsverluste
c+d an Produzenten
auf Produzenten:
verlieren h = Wohlfahrtsverluste
erhalten c+d
c+d > h = profitieren davon
Aber: Monopole können als "Belohnung" für Innovation sinnvoll sein, siehe Patentrecht, dass eine Monopolstellung temporär zusichert!
jedoch sollte man immer vorsichtig sein, Monopole in die Hand des Marktes zu geben!
Monopson#
Monoposonunternehmen: ein Nachfrager gegenübr vielen Anbietern, bspw. im Arbeitsmarkt
Gewinnkalkül des Monopsons: \(G(L) = p*X(L,K) - \bold{w(L)} * L - i*K-C_F\)
merke: Lohnsatz ist abhängig von Arbeitsangebot des Unternehmens
Monopsonoptimum: Ableitung nach L: $\( \frac{\partial G}{\partial L} = p*\frac{\partial X}{\partial L}- \frac{\partial w(L)}{\partial L} * L - w(L)*1 = 0 \\ \to \underbrace{p*\frac{\partial X}{\partial L}}_{WGP_L} = \underbrace{w + \frac{\partial w(L)} {\partial L} *L}_\text{Grenzausgaben} \)$
Erinnerung: normales Unternehmen: \(WGP_L = w\) für Optimum von L
graphische Darstellung: Monopson vs Polypol
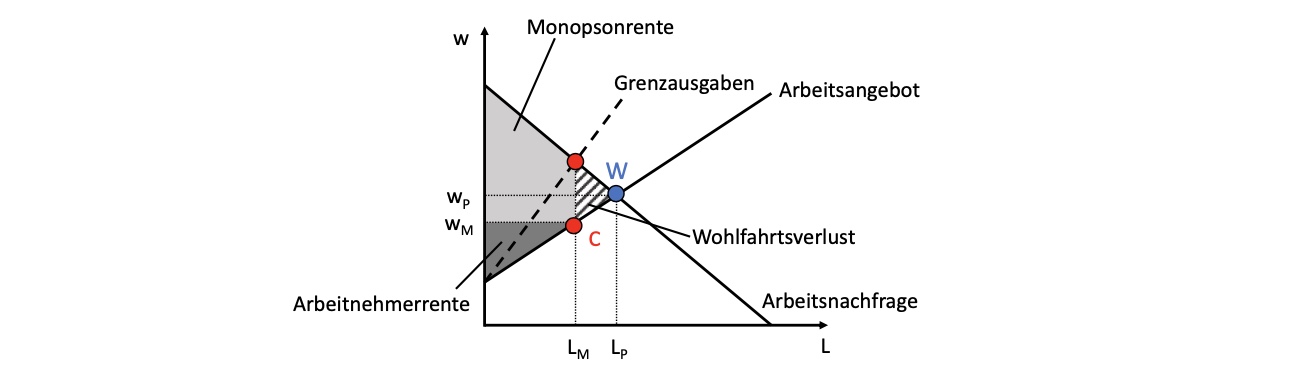
alternativ auch wieder Preisfixierung möglich
Oligopol#
generelles Modell von Polypol bis Monopol
Angebotsmarkt mit n wenigen Unternehmen
individuelle Produktionsmenge \(x_i\)
Angebotsmenge \(X = \sum_{i=1}^n x_i\)
Gewinnmaximierungskalkül $$ G(x_i) = p(X) * x_i - c * x_i \ \to \frac{\partial G}{\partial x_i} = \underbrace{\frac{\partial p}{\partial X} * \frac{\partial X}{\partial x_i} * x_i}_{T_1}
\underbrace{p1}_{T_2} -\underbrace{c1}_{T_3} = 0 $$
T1 = inframarginaler Umsatzeffekt < 0
T2 = marginaler Umsatzeffekt > 0
T3 = Kosten > 0
Optimum: \(T_2 = -T_1 + T_3\)
Symmetrieannahme#
im Gliehcgewicht alle Unternehmen gleiche Produktion $$ X^* = \sum_{i=1}^n x_i^* = n * x_i^* \to x_i = \frac{1}{n} X^* \ \text{Einsetzen in Gewinnableitung: }\ \frac{\partial G}{\partial x_i} = \frac{\partial p}{\partial X} * \frac{1}{n}* X^*
p -c = 0 $$
bei steigenden Zahlen von Unternehmen => sinkender T1
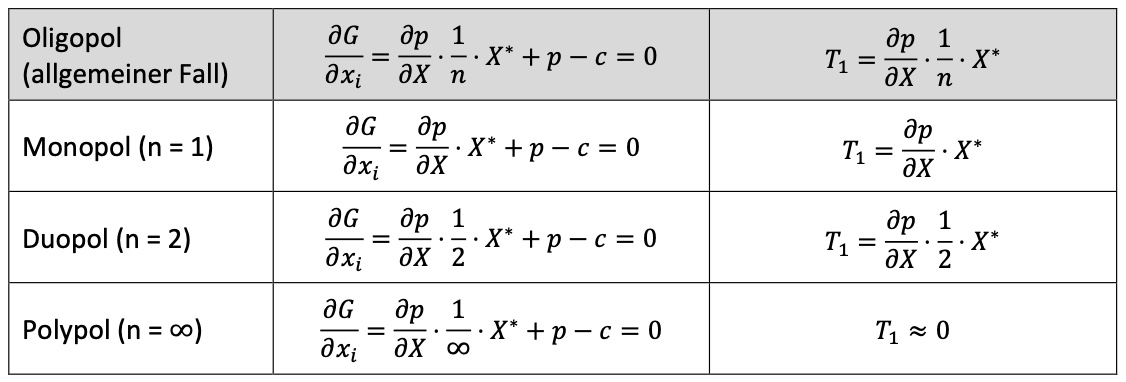
inframarginale Kosten nächstes Produktes tendieren gegen 0
Gleichgewichtsmengen bei verschiedenen Marktformen:
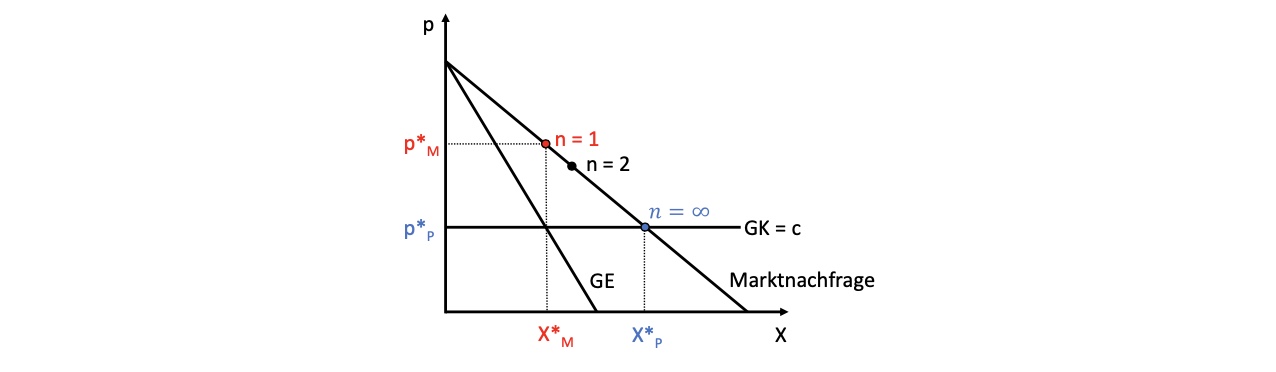
auf Monopolmarkt ist Menge die Hälfte des Optimums, mit steigenden Teilnehmern sinkt Preis und steigt Menge
Unternehmen kannibalisieren sich ihre Gewinne gegenseitig, da sie nicht exakt ihren Anteil an der Monopolmenge anbieten, sondern etwas mehr

Oligopol-Wettbewerb über Preisfixierung: Bertrand-Wettbewerb
Monopolistischer Wettbewerb#
Monopolunternehmen konkurrieren gegen Substitutionsgüter (bspw. Automobilanbieter)
Darstellung (kurz und langfristig):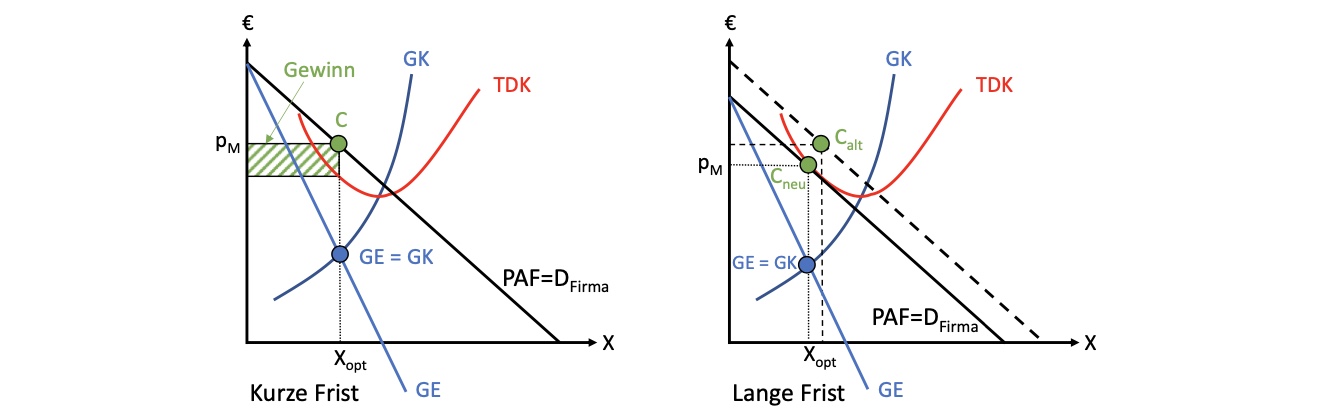
in der langen Frist nähern sich die Totalen Durchschnittskosten TDK der Preis-Absatz-Funktion PAF an => Nullgewinn
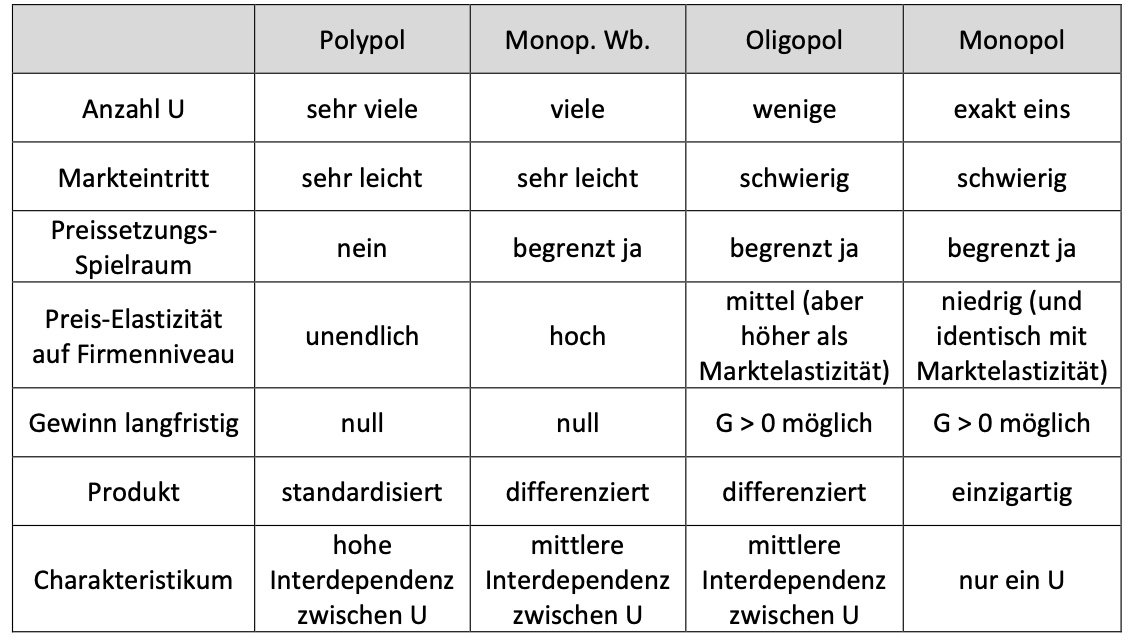
Überblick#
Charakteristika der verschiedenen Marktformen
Übung#
1. Marktgleichgewicht#
Kostenfunktion \(C(x) = 3x\)
Nachfrage: \(x=-2p+24\)
\(\to p(x) = -\frac{1}{2}x+12 \\\)
für Monopol Optimum: MC = ME (Grenzerlös)
allgemeines Optimum für Monopol:
$\(
\frac{\partial p(x)}{\partial x} x+p = MC
\)\(
Hier:
\)\(
C = 3x \to MC = 3 \\
E = p(x)\cdot x \to E=-\frac{1}{2}x^2+12x \\
ME = -x+12 \\
\)\(
Gleichsetzen
\)\(
ME = MC \\
-x+12 = 3 \implies \bold{x^* = 9} \\
p(9) = -\frac{1}{2}9+12 \to \bold{p^* = 7.5}
\)$
Graphisch: 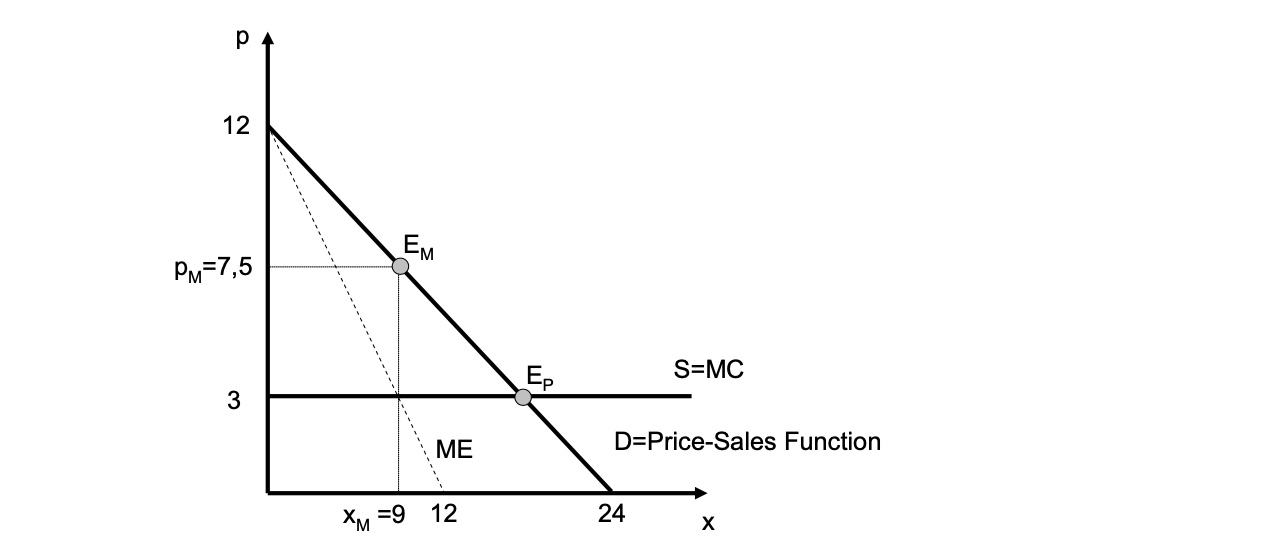
2. Wohlfahrtswirkungen#
normaler Markt: Nachfrage = MC $\( 3 = -0.5x + 12 \\ -9 = -0.5x \to x = 18 \\ p = -0.5*18+12 = 3 \)$ Renten in Monopol
Wohlfahrtsverlust: \(\frac{(18-9)*(7.5-3)}{2}\) (Fläche des Dreiecks) = \(20.25\)
Produzentenrente: \(9*(7.5-3) = 40.5\)
Konsumentenrente \(\frac{(12-7.5)*9}{2} = 20.25\)
Gesamtrente: \(67.5+20.25 = 60.75\)
Unterschied zu Polypol:
Produzentenrente = 0
Konsumentenrente: \(\frac{18*(12-3)}{2} = 81\)
Gesamtrente 81 > 60.75
Graphik: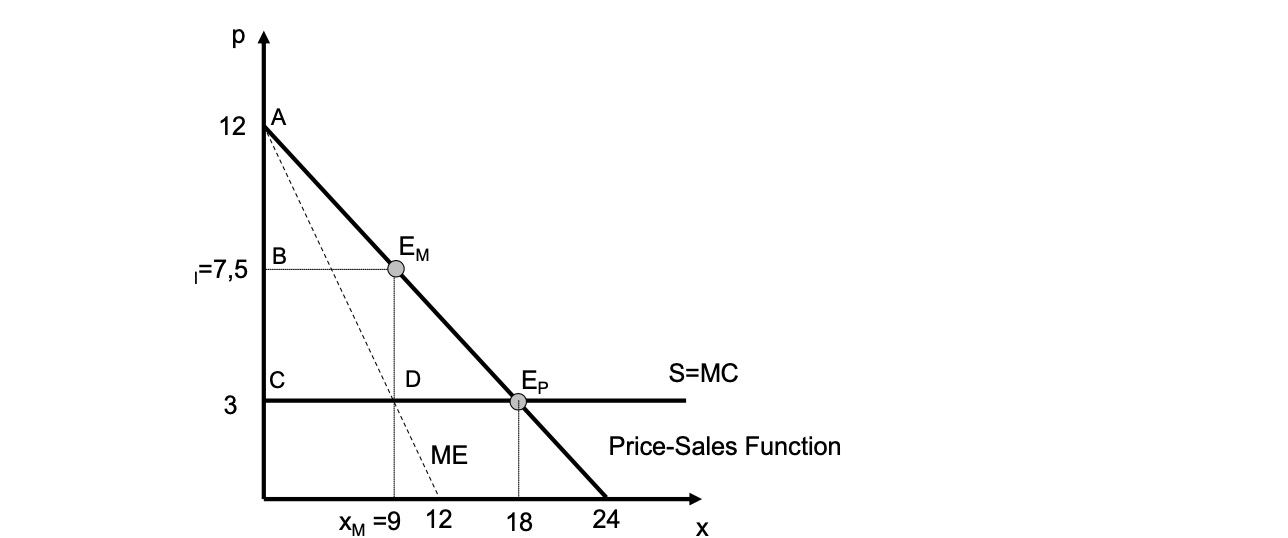
im Oligopol Punkt zwischen \(E_P\) und \(E_M\)
Besteuerung Stücksteuer#
Stücksteuer in Höhe des Monopolgewinns von Monopolist entrichtet
Bestimmung des Steuersatzes: $\( \frac{G}{x} = \frac{E-C}{x} = \frac{(9*7.5)-(9*3)}{9} = 4.5 \)\( Monopolist entrichtet => Erhöhung \)MC_{neu}=MC+4.5 = 7.5$
Gleichgewicht:
$\(
ME = -x+12 = 7.5 \to x = 4.5 \\
\to p(4.5) = -0.5*4.5 +12 = 9.75
\)$
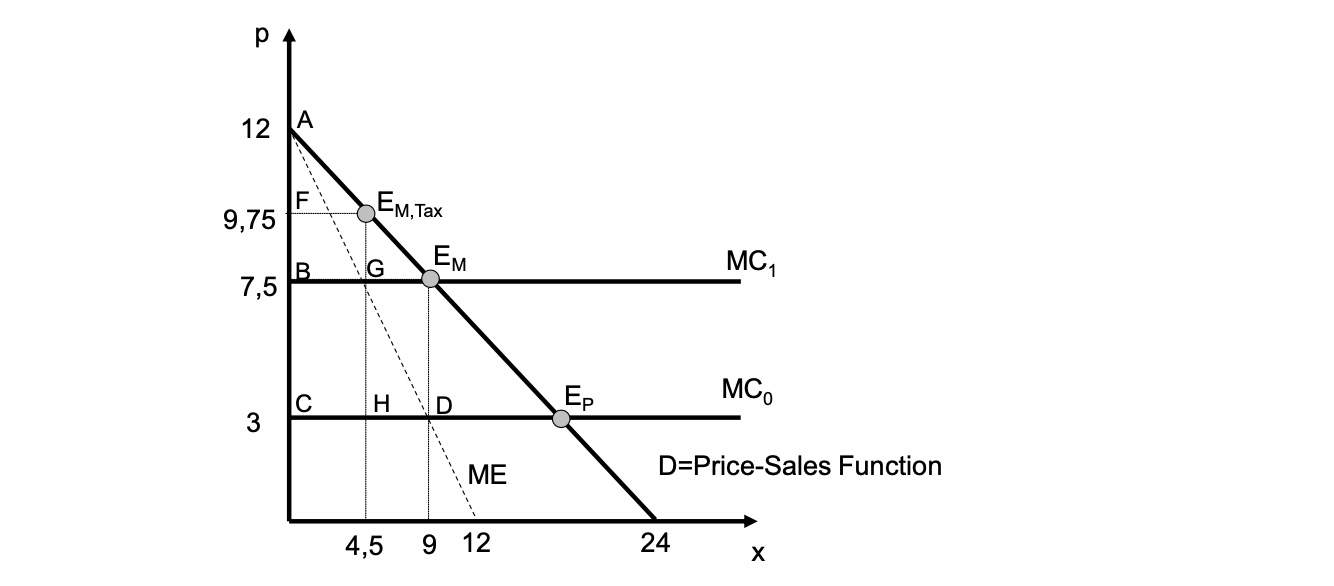
Kreislauf von andauernden Besteuerungen -> erneute Mengensenkung => nicht wohlfahrtswirksam!
Besteuerung Preisgrenze#
Preisgrenze von 4GE
Angebotsmenge p=4
$\(
x = -2p + 24 \\
x = 16
\)$
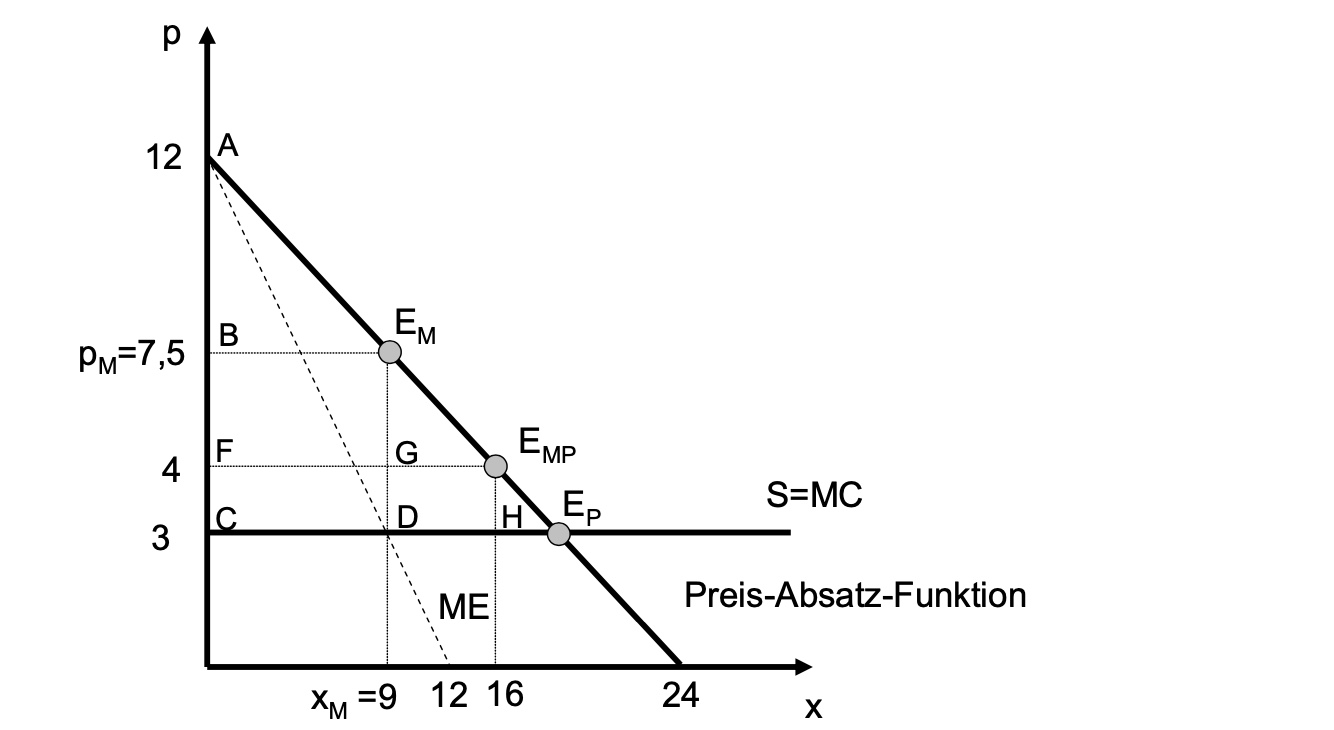
wirksamer!
Innovation#
Kostenfunktion auf \(C(x) = 2x\)
Wirkung Polypol: Nachfrage = MC $\( MC = 2 = -0.5x+12 \\ -10 = -0.5x \to x = 20 \\ p = -0.5*20+12 = 2 \)$
Konsumentenrente = Gesamtrente = \(\frac{20*(12-2)}{2}= 100\)
Produzentenrente = 0
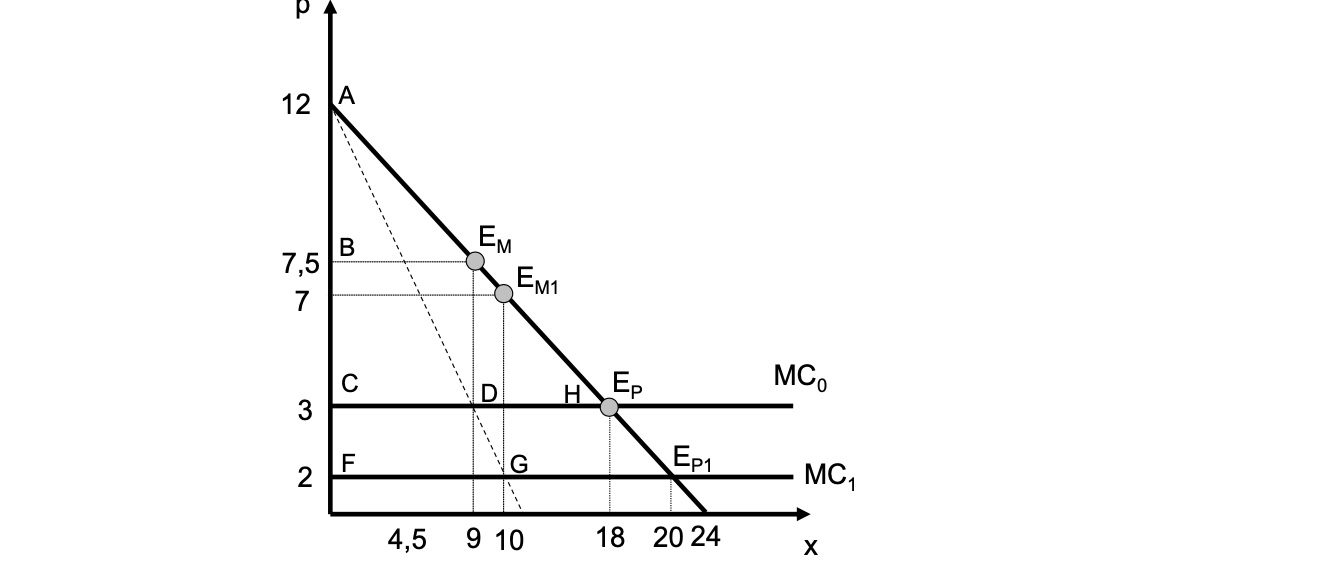
Wirkung Monopol $\( C = 2x \to MC = 2 \\ E = p(x)\cdot x \to E=-\frac{1}{2}x^2+12x \\ ME = -x+12 \\ \\ ME = MC \\ -x+12 = 2 \implies \bold{x^* = 10} \\ p(10) = -\frac{1}{2}10+12 \to \bold{p^* = 7} \)$
Monopolrente: \(10*(7-2) = 50; \Delta MR = 9.5\)
Konsumentenrente: \(\frac{10*(12-7)}{2} = 25\)
Monopole setzt Innovationsanreiz => Patente
Elastizität der Nachfrage#
Monopolgleichgewicht aus 1. $\( p = \frac{MC}{ 1- \frac{1}{|\varepsilon_{x,p}|}} \\ {|\varepsilon_{x,p}|} = \frac{1}{1- \frac{MC}{p}} \\ {|\varepsilon_{x,p}|} = \frac{1}{1-\frac{3}{7.5}} = 1.67 \)$ gewöhnliches Gut, also Elastizität (ohne Betragstriche) = -1.67
wenn Preiselastizität gegen unendlich: Polypolsituation, da MC=p
Beispiel:
Gegeben:
\(C(x) = 10x\)
Menge halbiert sich, wenn Preis um Viertel erhöht
Suche: Monopolpreis
Suche Elastizität
einsetzen in Formel
Polypolpreis: p=MC=10
Monopol = doppelter Preis