22.12.2022 Verhalten III: Zeitinkosistenz#
bisher: Exponentielles Diskontieren
Rationale Entscheidungen
Diskontfaktor (aber unterschiedlich bei Indiv.)
Zeitkonsistenz
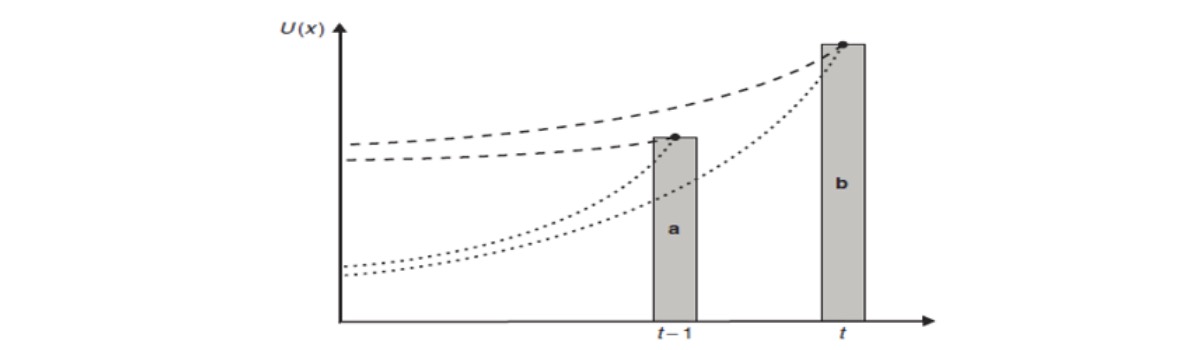
egal welcher Zeitraum, bleiben bei Entscheidung (a oder b)
Realität = komplizierter (bspw. Neujahrsvorsätze)
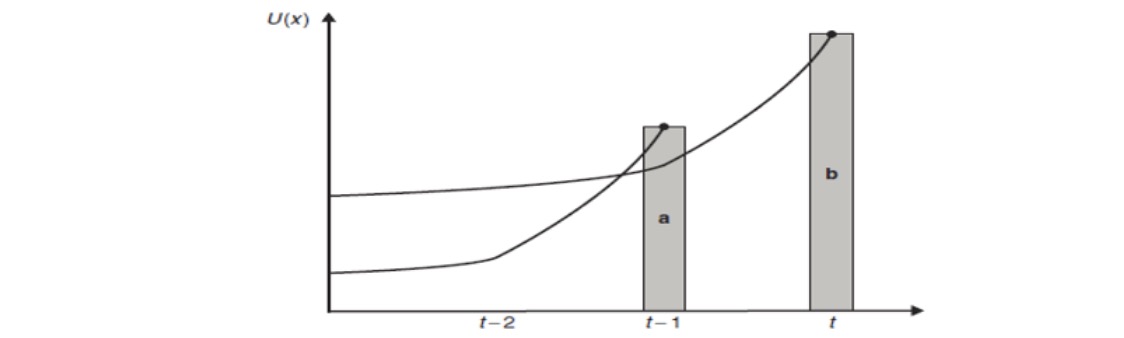
bei t-1 wählen a
bei t wählen b
Modellierung#
in exponentielles Diskontieren mit beta-Faktor $\( U(\bold{u}) = u_o + \beta \delta u_1 + \beta \delta^2 u_2 + \beta \delta^3 u_3 +... \\ = u_0 + \sum_i^\infty \beta \delta^i u_i \)$
weiterhin exponentiell ansteigender delta
aber konstanter beta
= quasi-hyperbolisches Diskontieren
\(\beta < 1\): stärkere Abzinsung der Zukunft = present-bias
Beta-Delta-Funktion:
gedludig / ungeduldig = Delta
Impulsiv = Beta
Beispiel#
Diät und Kuchen (soll ich auf einer Party Kuchen essen?)
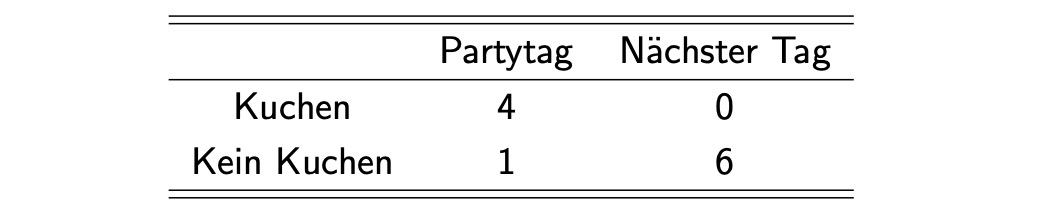
\(\beta = 1/2\)
\(\delta = 2/3\)
Nutzen am Tag davor: $$ U(Kuchen) = \overbrace{\frac{1}{2}}^{\beta} \cdot \overbrace{ \frac{2}{3}}^{\delta} \cdot 4
\frac{1}{2} \cdot \frac{2}{3}^2 \cdot 0 = 4/3\ U(\bar{Kuchen}) = \frac{1}{2} \cdot \frac{2}{3} \cdot1 + \frac{1}{2} \cdot \frac{2}{3}^2 \cdot 6 = 5/3 $$ = Entscheidung für kein Kuchen essen
Nutzen am Partytag: $\( U(Kuchen) = 4+ \frac{1}{2} \cdot \frac{2}{3} \cdot 0 = 4\\ U(\bar{Kuchen}) = 1 + \frac{1}{2} \cdot \frac{2}{3} \cdot 6 = 3 \)$ = Entscheidung für Kuchen essen
Selbstkontrolle#
Arten von Individuuen
naive I.: wissen nicht über ihre Zeitinkonsistenz
sophisticated I.: wissen über Inkosistenz
können bindende Entscheidungen für morgen heute treffen
Experimente von Ariely & Wertenbroch (2002) über Fristsetzung bei mehreren Abgaben
Optionen:
keine Fristen (Free Choice) = Ende des Semesters
selbstgesetzte Fristen (Own Choice)
externe Fristen (No Choice) = gleichmäßg verteilte Fristen
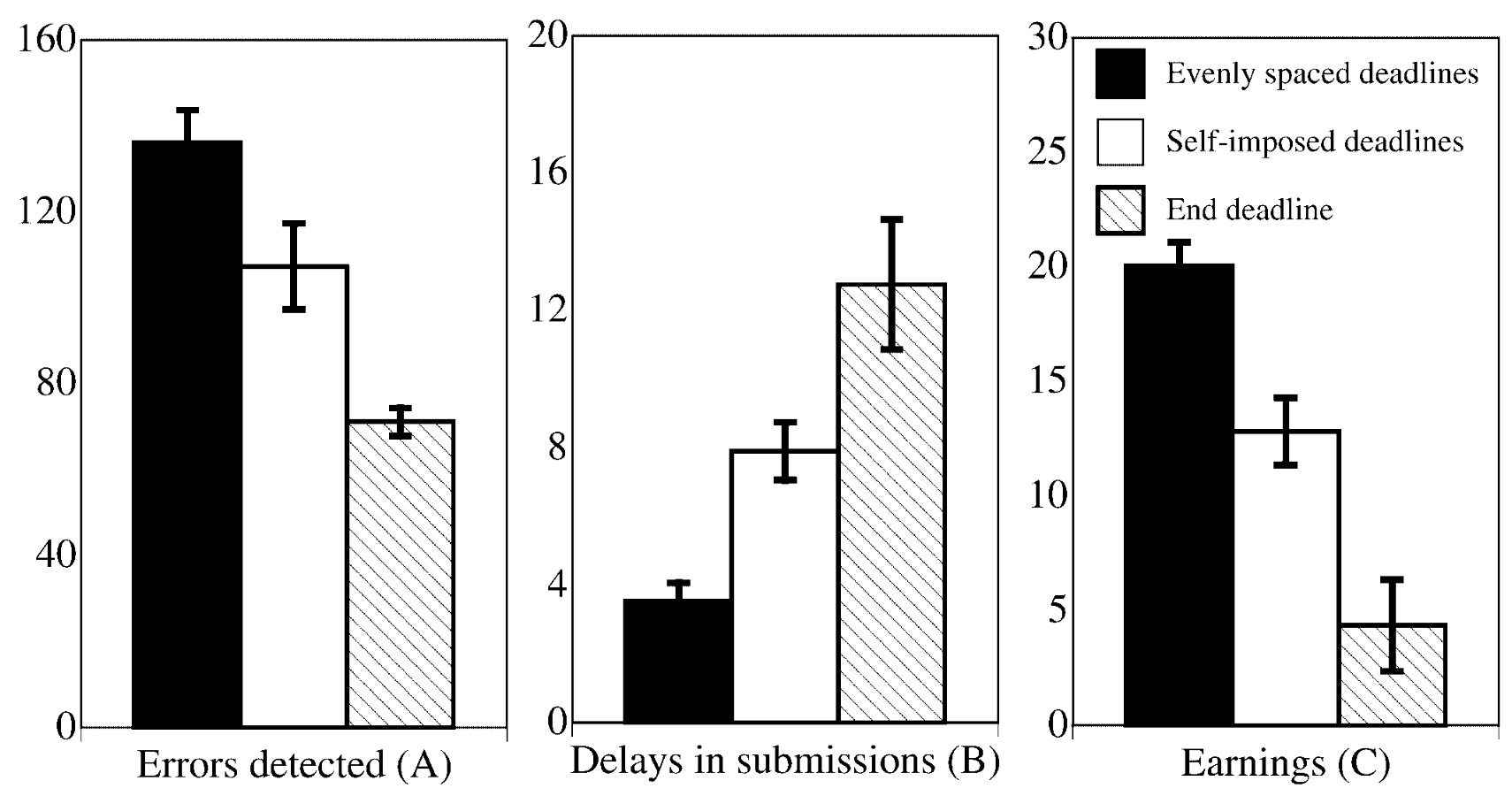
Nutzen: No Choice > Own Choice > Free Choice
Studierende wollen sich selber kontrollieren
ihre Methoden sind aber nicht optimal
also lieber externe Fristen setzen
Struktur und Präferenzen#
bisherige Annahme:
nur Barwert des Nutzens relevant, nicht Profil/ Verteilung / Reihenfolge
aber empirisch: „Beste zum Schluss“
Modellierung: Spitzen-End-Regel (nach Kahnemann)
peak-end-rule: Menschen bewerten Abfolge von Ereignissen, wie sich Moment extremsten Nutzens vs Ende der Abfolge angefühlt hat
= wenn das Ende angenehmer ist, dann wird gesamte Reihenfolge als angenehm wahrgenommen (unabhängig von Länge)
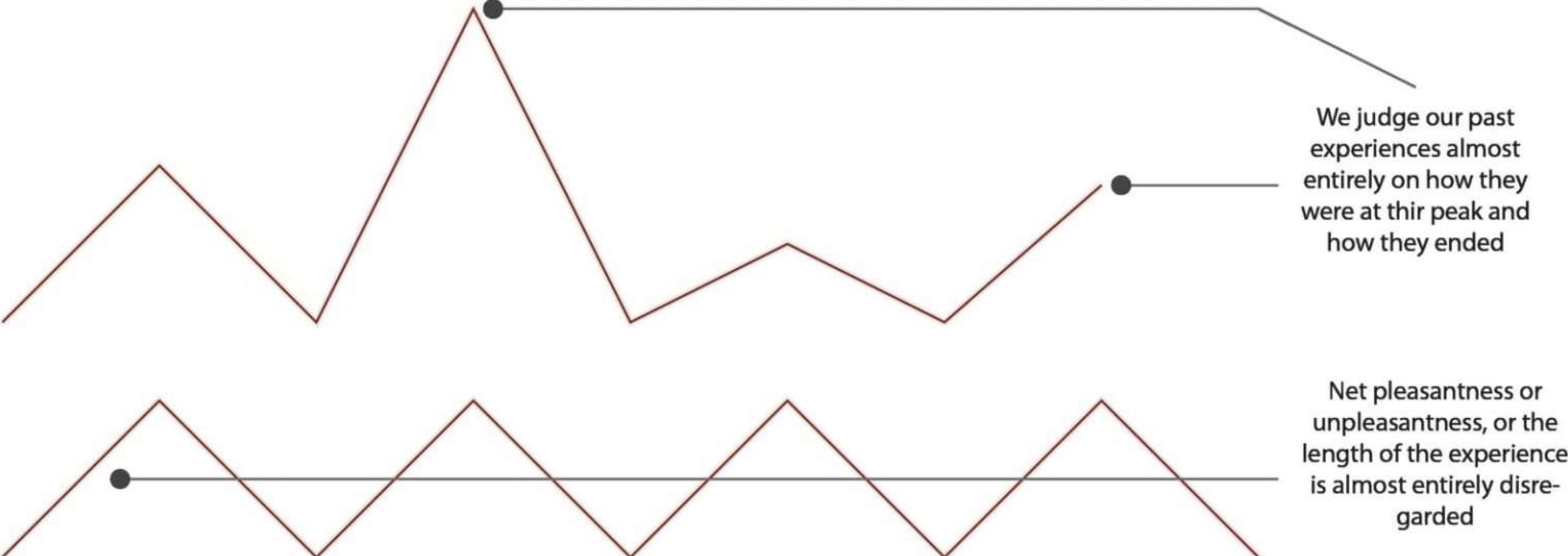
nutzbar für medizinische Prozeduren:
länger und am Ende angenehmer als
Ende mit abruptem Nachlassen des Schmerzes
Vorhersagen#
für intertemporale Entscheidungen = brauchen Präferenzen
verhaltensökonomische Effekte:
Unterschätzung Anpassungseffekte
Projektionsverzerrung
Tendenz, heutige Präferenz auf Zukunft projezieren (wer heute hungrig ist, ist es morgen wahrscheinlich nicht)
Überschätzung Nutzen Diversifikation
Unterschätzen Gewöhnungseffekt