06.11.2023 Externalities#
Externalities: situation, where ones party action affects others, but is not compensated
Example: Pollution, Education
Externalities = market failure => government intervention
Externality Theory#
Types:
positive / negative (Pollution / Education)
from production / from consumption (Pollution / Smoking)
Example: Steel Company
Production of steel and sludge
1 unit of sludge for every unit of steel
sludge directed into stream, kills fish from fishers
Externalities: SMC \(\neq\) PMC
Private Marginal Cost (PMC): direct cost to produce one good
Social Marginal Cost (SMC): PMC + costs imposed on others
Example: 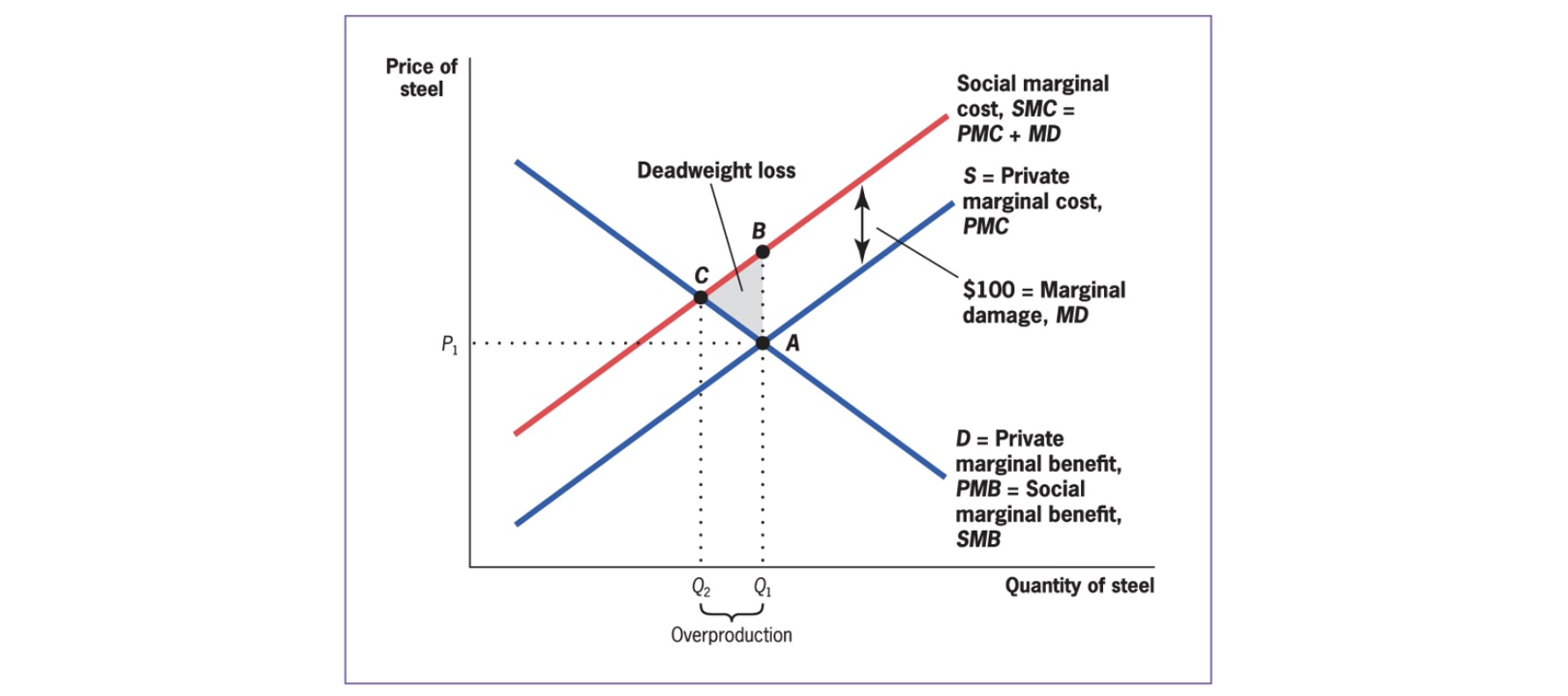
Types of Externalities:
negative production: SMC > PMC
negative consumption: SMB < PMB (Private Marginal Benefit)
…
Solution: internalize Externalities
private negotiation
government solutions
Private Sector#
Coase Theorem: well defined property rights + negotiations => socially optimal market quantity
Example:
Fishers own the property rights
negotiate compensation with steel plant
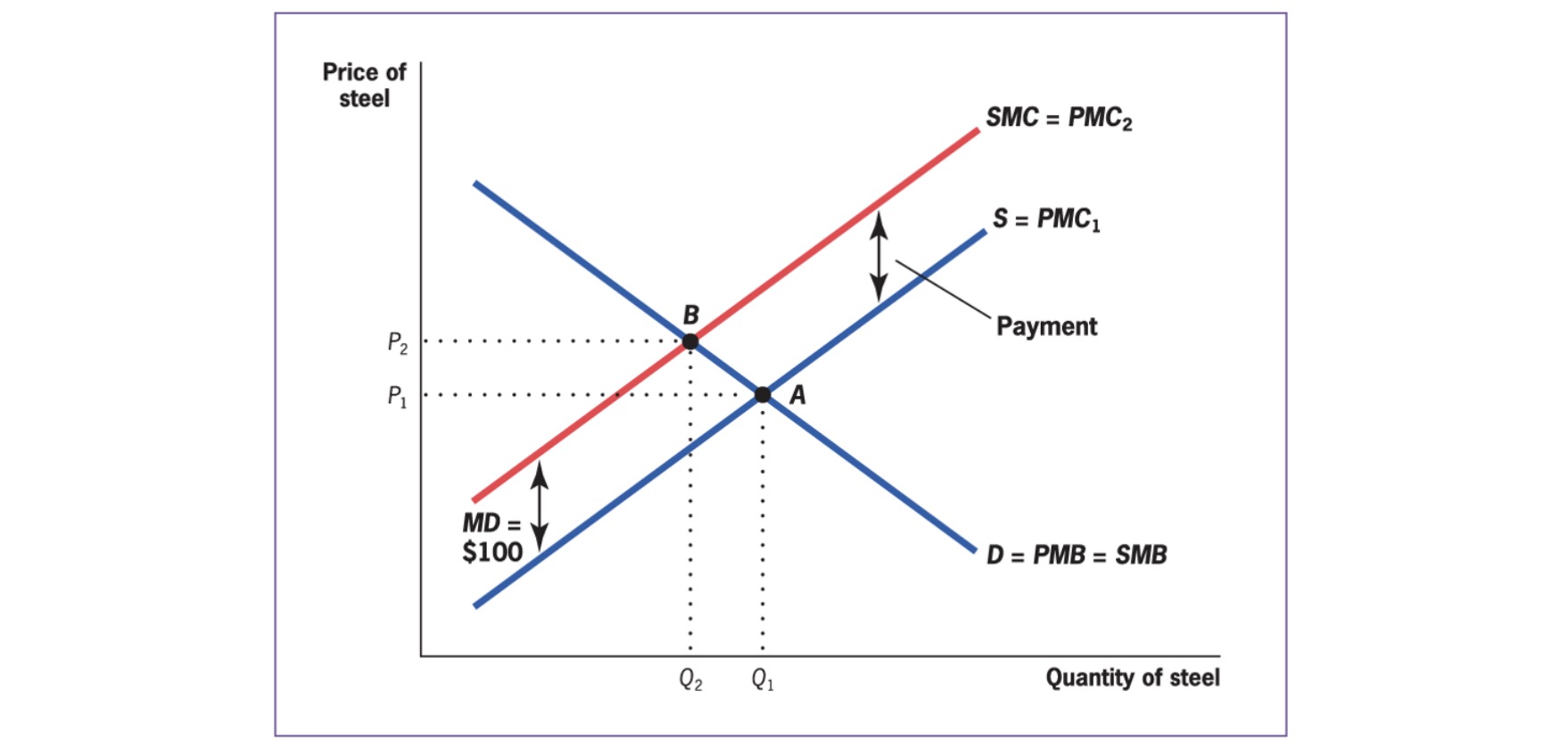
Important: Efficient solution does not depend who owns the property rights!
Problems: (especially with many people)
Assignment Problem
who causes the damage?
how large is the damage?
Holdout Problem
shared ownership of rights = veto options
may demand enormous payments
Free Rider Problem
Transaction Costs / Negotiationg Problems
=> Coase only works with specific problems!
Public Interventions#
Instruments:
Taxation / Subsidies
internalize externality
correct tax = Pigou Tax
Regulation
regulate Quantities
complicated information needed
Price-Based Approach vs Quantity Based Approach
Distinction#
Right Amount of Pollution
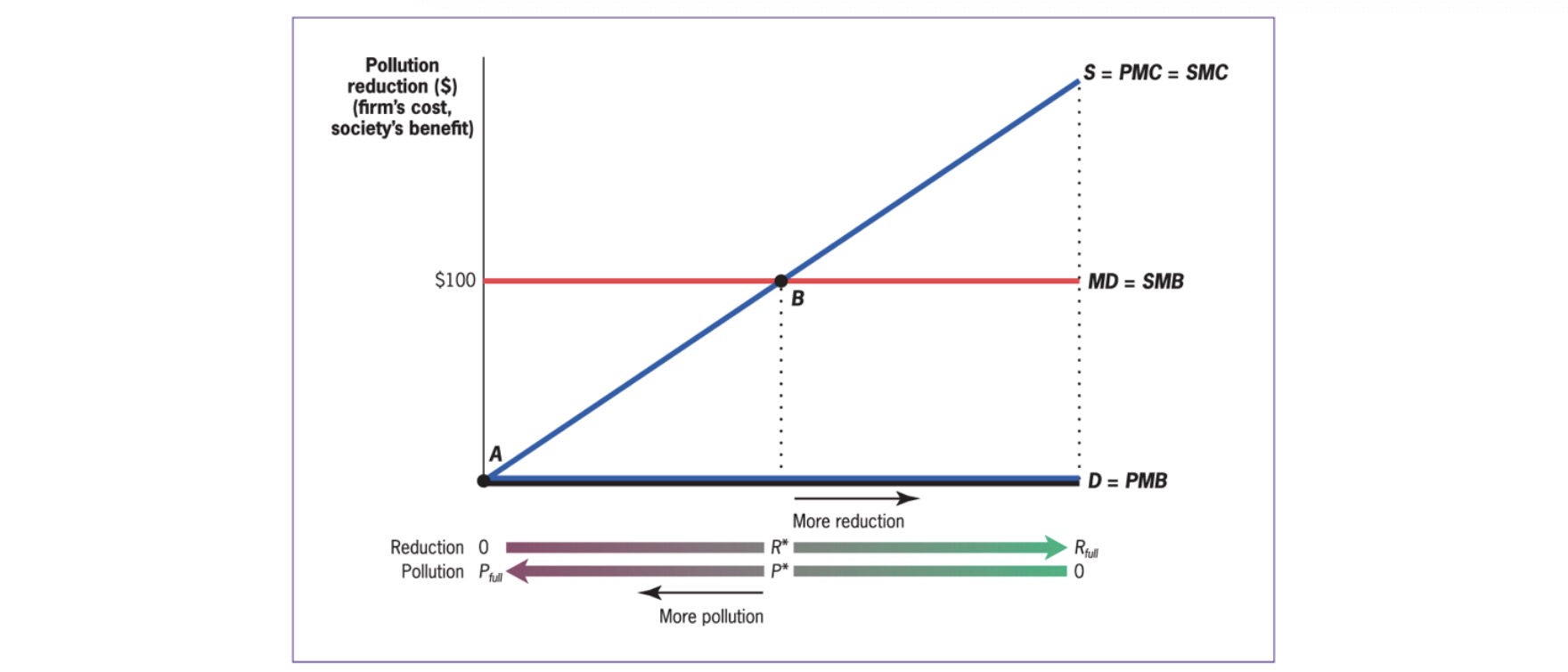
A = free market
B = socially optimal: SMC = SMB
Example 1: Multiple Plants with differenct reduction costs
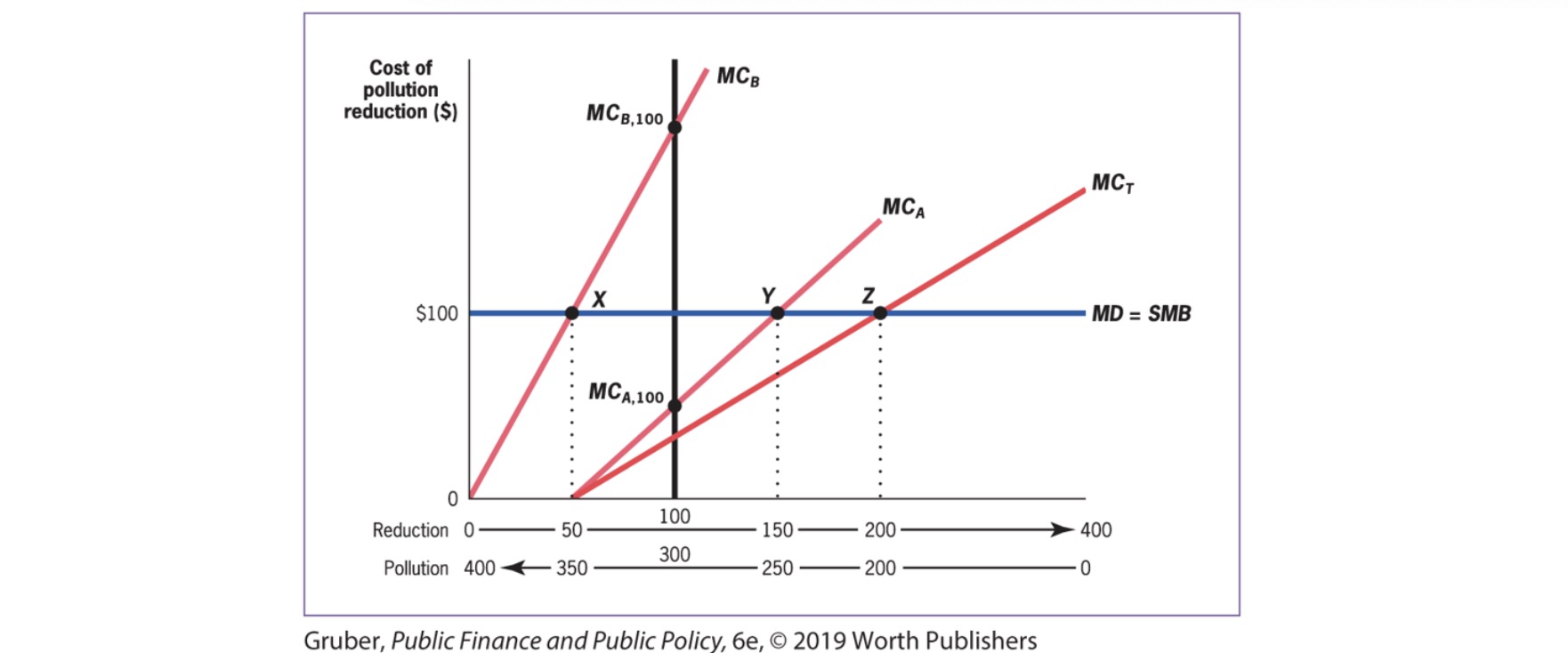
blue line = Tax (efficient)
black line = Regulation
Example 2: unvertainty about costs
high SMB of Reduction => Quantity Based Approach (nuclear leakage)
Low SMB of Reduction => Price Based Approach (kg of carbon)
High SMB:
Assumption of MC1
C = Regulation and Tax
if real MC = MC2
E = Tax
A = Regulation
DWL Regulation < DWL Tax
=> when Quantity is important use Regulation, else taxes
Tutorial: Addition of Demands#
Vertical Summation = Add up at Quantity Q (Public Good)
Horizontal Summation = Add up Demands at Price P
Example Horizontal:
A: \(Q = 21-6P\)
B: \(Q = 6-3P\)
Addition of the Quantites at given Price $\( Q_1 + Q_2 = (21-6P) + (6-3P) = 27-9P \\ 9P = 27 \to P = 3 - \frac{ 1 }{9}Q \)$
Example Vertical
Solve indivudally for P (Demands from above)
A: \(P = \frac{ 7 }{2} - \frac{ 1 }{6}Q\)
B: \(P = 2 - \frac{ 1 }{3}Q\)
Sum up
Bike Paths Example#
individual Bike Path Demand
A: \(Q=24-4P\)
B: \(Q = 14-P\)
C: \(Q = 5-1/3P\)
Marginal Cost of one Path = 18
Version 1
town decides to tax evenly
asks residents, highest number answered gets build
\(MC = a+b+c\), here (a=b=c)
18/3 = 6 Cost Units
Demands at this Price (input P=6)
A: Q=0
B: Q=8
C: Q=3
=> Build 8 Paths
Version 2: Social Optimum
solve every Demand for P
sum Up => SMB
SMB = MC = 18, solve for Q
insert Q into individual Demand Functions